Using Transformations to Investigate Functions
Let’s investigate how transformations may be applied to functions:
Example 1:
Remember to utilize your graphing calculator to get a feel for the function and the changes.
Transform the function f (x) = ex with a vertical stretch by a factor of 3, followed by a translation 5 units to the right.
Write an equation for the transformed function.
Graph the transformed function.
Answer:
Remember:
• a vertical stretch will change the y values.
• a translation to the right will affect the x values.
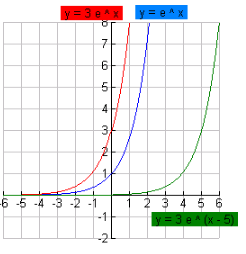 1
1
The original function, f (x), (the parent function) is graphed in blue.
f (x) with a vertical stretch by a factor of 3 is graphed in red.
f (x) with the vertical stretch AND the translation of 5 units to the right is graphed in green.
The final transformed function is represented by the equation
f (x) = 3 e (x-5)
Example 2:
Given f (x) = x2 – 2x
A. Determine an expression for h(x), if h(x) = f (-x).
B. Determine an expression for g(x), if g(x) is represented by the rotation of 180º of f (x) about the origin.
C. Rotate f (x) 90º about the origin. Find the coordinates of the point(s) for which x = -1, under the rotation.
Answer:
Things to remember:
• Rotation of 180º r180º(x,y) = (-x,-y)
• Rotation of 90º r90º(x,y) = (-y,x)
• Examine points that are easily readable from the original graph.
• Again, your graphing calculator could assist you in finding your answers.
• While graphs are NOT required in this problem, they certainly help in analyzing the problem.
The original function, f(x), is graphed in blue.
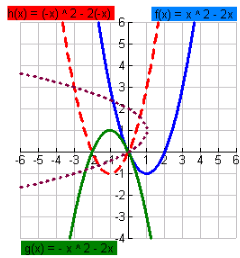
A. the expression for h(x) is
h(x) = (-x)2 -2(-x) = x2 +2x
B. the expression for g(x) is
g(x) = -x2 -2x
C. the 90º rotation is indicated by the dotted line. The coordinates for which x = -1 are (-1, -0.414) and
(-1, 2.414) *
* x = -1 under the rotation is equivalent to y = 1 under the original graph.
Therefore, we are interested in x2 – 2x = 1 which gives x2 – 2x – 1 = 0.
Use your graphing calculator to solve. One possible calculator solution method is shown below:
Y1=x2 – 2x – 1
Y2 = 0
Use 2nd – Calc – #5 Intersect to find the points of intersection
