Undefined Algebraic Fractions
A fraction is said to be undefined (or have no meaning) when the denominator = 0.
Consider: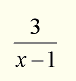 Solution: determine when the denominator equals 0.
Solution: determine when the denominator equals 0.
Set the denominator = 0 and solve.
The NUMERATOR IS IGNORED. It is only necessary to investigate the denominator.
The solution to the above example is: x – 1 = 0, or x = 1.
The fraction is undefined when x = 1.
Domain: All Real numbers but not x = 1.
Notation: {x: x ≠ 1} “all x’s such that x ≠ 1”.
Example 1:
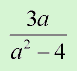
Set the denominator = 0 and solve.
a2 – 4 = 0
a2 = 4
a = ± 2
Domain: All Real numbers but not a = 2 nor a = -2.
Notation: {a: a ≠ ± 2}
Example 2:
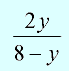
Set: 8 – y = 0
8 = y
Domain: All Real numbers, except y = 8.
Example 3:
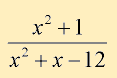
Set: x2 + x – 12 = 0
(x – 3)(x + 4) = 0
x – 3 = 0; x = 3
x + 4 = 0; x = -4
Domain: All Real numbers, but not x = 3 and not x = -4.
