What are the Types of Relations in Set Theory
Relations
Definition :
Let A and B be two non-empty sets, then every subset of A × B defines a relation from A to B and every relation from A to B is a subset of A × B.
Let R ⊆ A × B and (a, b) ∈ R. Then we say that a is related to b by the relation R and write it as a R b. If (a, b) ∈ R, we write it as a R b.
(1) Total number of relations : Let A and B be two non-empty finite sets consisting of m and n elements respectively. Then A × B consists of mn ordered pairs. So, total number of subset of A × B is 2mn. Since each subset of A × B defines relation from A to B, so total number of relations from A to B is 2mn. Among these 2mn relations the void relation f and the universal relation A × B are trivial relations from A to B.
(2) Domain and range of a relation : Let R be a relation from a set A to a set B. Then the set of all first components or coordinates of the ordered pairs belonging to R is called the domain of R, while the set of all second components or coordinates of the ordered pairs in R is called the range of R.
Thus, Dom (R) = {a : (a, b) ∈ R} and Range (R) = {b : (a, b) ∈ R}.
Inverse relation
Let A, B be two sets and let R be a relation from a set A to a set B. Then the inverse of R, denoted by R–1, is a relation from B to A and is defined by R–1 = {(b, a) : (a, b) ∈ R}.
Clearly (a, b) ∈ R ⟺ (b, a) ∈ R–1. Also, Dom (R) = Range (R–1) and Range (R) = Dom (R–1)
Example : Let A = {a, b, c}, B = {1, 2, 3} and R = {(a, 1), (a, 3), (b, 3), (c, 3)}.
Then,
- R–1 = {(1, a), (3, a), (3, b), (3, c)}
- Dom (R) = {a, b, c} = Range (R–1)
- Range (R) = {1, 3} = Dom (R–1)
Types of relations
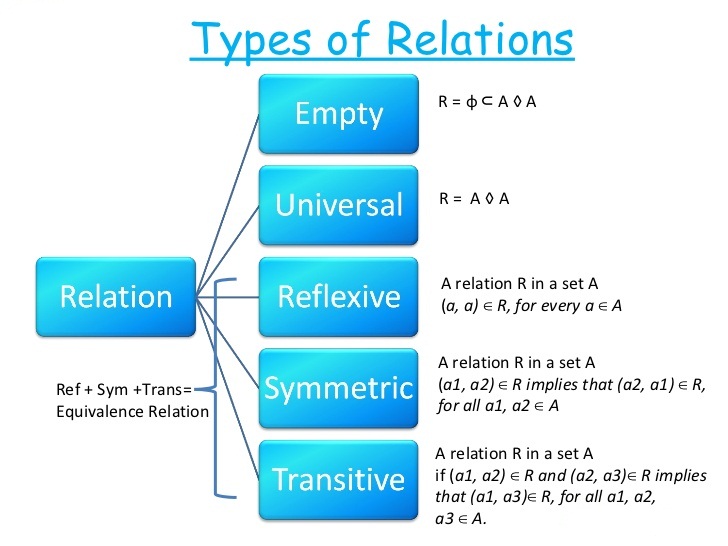
(1) Reflexive relation : A relation R on a set A is said to be reflexive if every element of A is related to itself.
Thus, R is reflexive ⟺ (a, a) ∈ R for all a ∈ A.
Example : Let A = {1, 2, 3} and R = {(1, 1); (1, 3)}
Then R is not reflexive since 3 ∈ A but (3, 3) ∉ R
A reflexive relation on A is not necessarily the identity relation on A.
The universal relation on a non-void set A is reflexive.
(2) Symmetric relation : A relation R on a set A is said to be a symmetric relation iff (a, b) ∈ R ⇒ (b, a) ∈ R for all a, b ∈ A
i.e., a R b ⇒ b R a for all a, b ∈ A.
it should be noted that R is symmetric iff R–1 = R
The identity and the universal relations on a non-void set are symmetric relations.
A reflexive relation on a set A is not necessarily symmetric.
(3) Anti-symmetric relation : Let A be any set. A relation R on set A is said to be an anti-symmetric relation iff (a, b) ∈ R and (b, a) ∈ R ⇒ a = b for all a, b ∈ A.
Thus, if a ≠ b then a may be related to b or b may be related to a, but never both.
(4) Transitive relation : Let A be any set. A relation R on set A is said to be a transitive relation iff (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R for all a, b, c ∈ A i.e., a R b and b R c ⇒ a R c for all a, b, c ∈ A.
Transitivity fails only when there exists a, b, c such that a R b, b R c but a R c.
Example : Consider the set A = {1, 2, 3} and the relations
R1 = {(1, 2), (1,3)}; R2 = {(1, 2)}; R3 = {(1, 1)};
R4 = {(1, 2), (2, 1), (1, 1)}
Then R1, R2, R3 are transitive while R4 is not transitive since in R4, (2, 1) ∈ R4; (1,2) ∈ R4 but (2, 2) ∉ R4.
The identity and the universal relations on a non-void sets are transitive.
(5) Identity relation : Let A be a set. Then the relation IA = {(a, a) : a ∈ A} on A is called the identity relation on A.
In other words, a relation IA on A is called the identity relation if every element of A is related to itself only. Every identity relation will be reflexive, symmetric and transitive.
Example : On the set = {1, 2, 3}, R = {(1, 1), (2, 2), (3, 3)} is the identity relation on A .
It is interesting to note that every identity relation is reflexive but every reflexive relation need not be an identity relation.
(6) Equivalence relation : A relation R on a set A is said to be an equivalence relation on A iff
(i) It is reflexive i.e. (a, a) ∈ R for all a ∈ A
(ii) It is symmetric i.e. (a, b) ∈ R ⇒ (b, a) ∈ R, for all a, b ∈ A
(iii) It is transitive i.e. (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R for all a, b, c ∈ A.
Congruence modulo (m) : Let m be an arbitrary but fixed integer. Two integers a and b are said to be congruence modulo m if a – b is divisible by m and we write a ≡ b (mod m).
Thus a ≡ b (mod m) ⟺ a – b is divisible by m. For example, 18 ≡ 3 (mod 5) because 18 – 3 = 15 which is divisible by 5. Similarly, 3 ≡ 13 (mod 2) because 3 – 13 = –10 which is divisible by 2. But 25 ≠ 2 (mod 4) because 4 is not a divisor of 25 – 3 = 22.
The relation “Congruence modulo m” is an equivalence relation.
Equivalence classes of an equivalence relation
Let R be equivalence relation in A(≠ ϕ). Let a ∈ A. Then the equivalence class of a, denoted by [a] or is defined as the set of all those points of A which are related to a under the relation R. Thus [a] = {x ∈ A : x R a}.
It is easy to see that
- b ∈ [a] ⇒ a ∈ [b]
- b ∈ [a] ⇒ [a] = [b]
- Two equivalence classes are either disjoint or identical.
Composition of relations
Let R and S be two relations from sets A to B and B to C respectively. Then we can define a relation SoR from A to C such that (a, c) ∈ SoR ⟺ ∃ b ∈ B such that (a, b) ∈ R and (b, c) ∈ S.
This relation is called the composition of R and S.
For example, if A = {1, 2, 3}, B = {a, b, c, d}, C={p, q, r, s} be three sets such that R = {(1, a), (2, b), (1, c), (2, d)} is a relation from A to B and S = {(a, s), (b, r), (c, r)} is a relation from B to C. Then SoR is a relation from A to C given by SoR = {(1, s) (2, r) (1, r)}
In this case RoS does not exist.
In general RoS ≠ SoR. Also (SoR)–1 = R–1oS–1.
