Trigonometry: Solving for a Side

Trigonometry: Solving for a Side

The word ‘trigonometry’ is derived from the Greek words ‘tri’(meaning three), ‘gon’ (meaning sides) and ‘metron’ (meaning measure).
Trigonometry is the study of relationships between the sides and angles of a triangle.

Applications of trigonometry:
There are an enormous number of uses of trigonometry and trigonometric functions.

1. Early astronomers used it to find out the distances of the stars and planets from the Earth.
2. In geography to measure distances between landmarks, and in satellite navigation systems.
   
3. Even today, most of the technologically advanced methods used in Engineering and Physical Sciences are based on trigonometrical concepts.
4. The sine and cosine functions are fundamental to the theory of periodic functions such as those that describe sound and light waves.

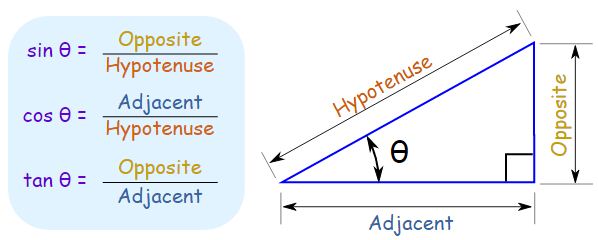
Basic Trigonometry Rules:

1. These formulas ONLY work in a right triangle.
2. The hypotenuse is always across from the right angle.
3. Questions usually ask for an answer to the nearest units.
4. You will need a scientific or graphing calculator.

Using Trigonometric Functions to Find a Missing Side

How to set up and solve a trigonometry problem:

Set up the diagram:

1. Draw a diagram depicting the situation, if one is not given.
2. Place the angle degrees INSIDE the triangle.
3. Imagine standing at the reference angle.
4. LABEL the triangle with o, h, and a.
   o – opposite side (the side across from you)
   h – hypotenuse (across from the right angle)
   a – adjacent side (the leftover side)
5. “Pair Up” the values.
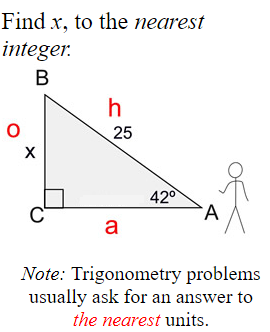
   The h pairs with the 25.
   The o pairs with the x.
   The a stands alone, which means the a is not involved in the solution to this problem. Cross it out!
   This problem deals with o and h.
   

Set up the formula:

1. Since this problem deals with o and h, we use the sine function since it also deals with o and h.
2. Replace A with the angle degrees.
3. Replace o and h with their companion terms.
4. Use your scientific/graphing calculator to determine the value of sin 42º. (On most graphing calculators, set the mode to degree and press the sin key followed by 42. Most scientific calculators will reverse this order: press 42 first, followed by the sin key.
5. Solve the equation algebraically. In this problem, cross multiply and solve for x. (When x is on top, you multiply to get the answer. When x is on the bottom, you will divide to get the answer – see example below.)
6. Round answer to desired value.
   

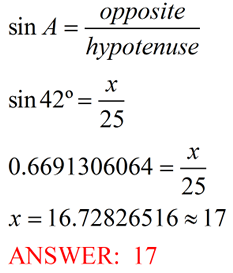
Example 2: IIn right triangle ABC, ∠C is the right angle, BC = 17 and angle B = 35º.
Find BA to the nearest tenth.
Solution:
Set up the diagram and the formula in the same manner as was done in
Example 1. You should arrive at the drawing and the formula shown here.

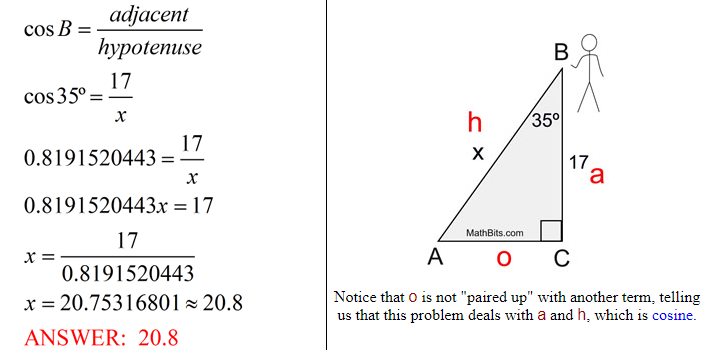
Hint: If you are having a problem solving the equation algebraically, remember that when x is on the bottom, you must divide to arrive at your answer. The division is always “divide BY the trig value decimal”.

Hint: Be sure your answer MAKES SENSE!!! The hypotenuse is always the largest side in a right triangle. So, our answer of 26.50 makes sense – it is bigger than the leg of 20.