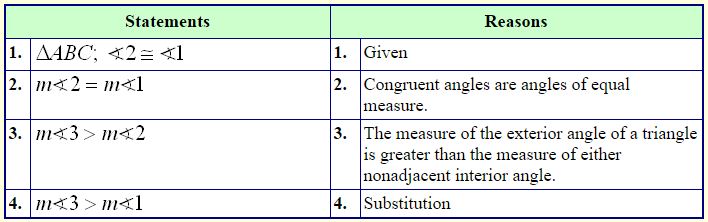
Triangle Inequalities
Theorem 1:
The sum of the lengths of any two sides of a triangle must be greater than the third side.
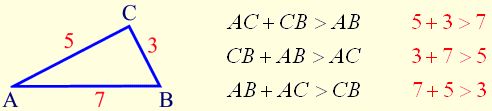
If these inequalities are NOT true, you do not have a triangle!
Example
Suppose we know the lengths of two sides of a triangle, and we want to find the “possible” lengths of the third side.
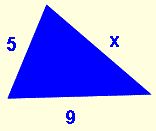According to our theorem, the following 3 statements must be true:
- 5 + x > 9
So, x > 4 - 5 + 9 > x
So, 14 > x - x + 9 > 5
So, x > -4
(no real information is gained here since the lengths of the sides must be positive.)
Putting these statements together, we get that x must be greater than 4, but less than 14. So any number in the range 4 < x < 14 can represent the length of the missing side of our triangle.
Theorem 2:
In a triangle, the longest side is across from the largest angle.
Theorem 3:
In a triangle, the largest angle is across from the longest side.
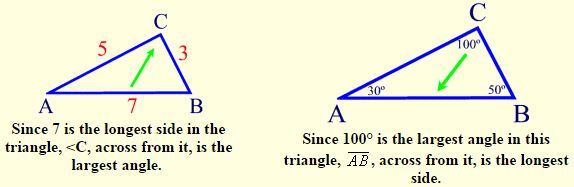
These theorems can be modified to apply to a discussion of only two angles within the triangle:
Theorem: In a triangle, the longer side is across from the larger angle.
Theorem: In a triangle, the larger angle is across from the longer side.
Example
Suppose we want to know which side of this triangle is the longest.
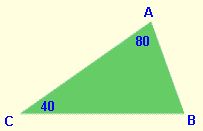Before we can utilize our theorem, we need to know the size of <B. We know that the 3 angles of the triangle add up to 180°.
We have now found that <B measures 60°. According to our theorem, the longest side will be across from the largest angle.
80 + 40 + x = 180
120 + x = 180
x = 60
Now that we know the measures of all 3 angles, we can tell that <A is the largest. This means the side across from <A, side \(\overline { CB }\), is the longest side.
Theorem 4:
The measure of the exterior angle of a triangle is greater than the measure of either nonadjacent interior angle.
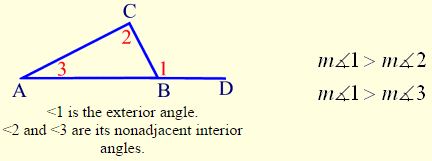
Example
Suppose we are faced with the following proof:
