Translations
A translation “slides” an object a fixed distance in a given direction. The original object and its translation have the same shape and size, and they face in the same direction. A translation creates a figure that is congruent with the original figure and preserves distance (length) and orientation (lettering order). A translation is a direct isometry.
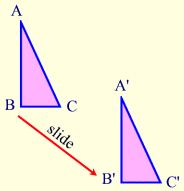Properties preserved (invariant) under a translation:
- distance (lengths of segments are the same)
- angle measures (remain the same)
- parallelism (parallel lines remain parallel)
- colinearity (points stay on the same lines)
- midpoint (midpoints remain the same in each figure)
- orientation (lettering order remains the same)
Definition: A translation (notation Ta,b) is a transformation of the plane that slides every point of a figure the same distance in the same direction.
Ta,b(x, y) = (x+a, y+b)
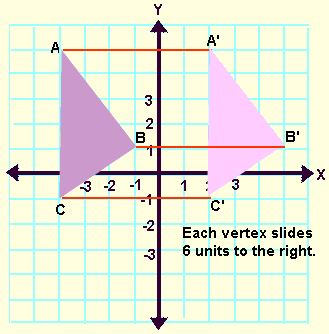
Translations in the Coordinate Plane:
In the example below, notice how each vertex moves the same distance in the same direction.
In this next example, the “slide” (translation) moves the figure 7 units to the left and 3 units down.
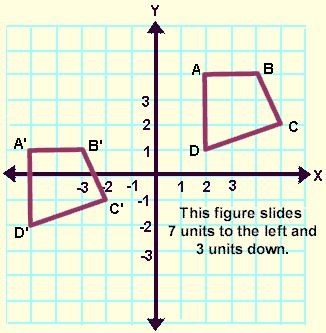There are several ways to indicate that a translation is to occur:
- Description: 7 units to the left and 3 units down. (A verbal description of the translation is given.)
- Mapping: (x, y)→(x-7, y-3)
(This is read: “the x and y coordinates will be translated into x-7 and y-3”. Notice that adding a negative value (subtraction), moves the image left and/or down, while adding a positive value moves the image right and/or up.) - Notation:
(The -7 tells you to subtract 7 from all of your x-coordinates, while the -3 tells you to subtract 3 from all of your y-coordinates.)
This may also be seen as T-7,-3(x,y) = (x -7,y – 3). - Vectors:
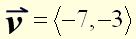
(A vector, a directed line segment, may also be used to show the movement of a translation. See more about vectors and translations.)