What is Transformation of Axes?
(1) Shifting of origin without rotation of axes :
Let P ≡ (x, y) with respect to axes OX and OY.
Let O’ ≡ (α, β) with respect to axes OX and OY and let P ≡ (x’, y’) with respect to axes O’X’ and O’Y’, where OX and O’X’ are parallel and OY and O’Y’ are parallel.
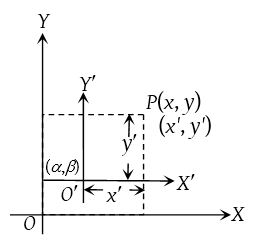Then x = x’ + α, y = y’ + β
or x’ = x – α, y’ = y – β
Thus if origin is shifted to point (α, β) without rotation of axes, then new equation of curve can be obtained by putting x + α in place of x and y + β in place of y.
(2) Rotation of axes without changing the origin :
Let O be the origin. Let P ≡ (x, y) with respect to axes OX and OY and let P ≡ (x’, y’) with respect to axes OX¢ and OY¢ where ∠X’OX = ∠Y’OY = θ.
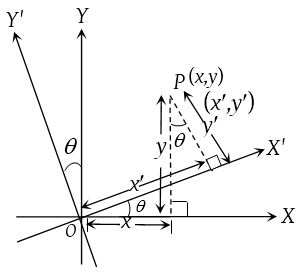then x = x’ cos θ – y’ sin θ
y = x’ sin θ + y’ cos θ
and x’ = x cos θ + y sin θ
y’ = –x sin θ + y cos θ
The above relation between (x, y) and (x’, y’) can be easily obtained with the help of following table
| x ↓ | y ↓ | |
| x’ → | cos θ | sin θ |
| y’ → | – sin θ | cos θ |
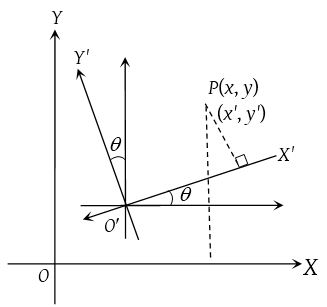
(3) Change of origin and rotation of axes :
If origin is changed to O’(α, β) and axes are rotated about the new origin O’ by an angle θ in the anti-clockwise sense such that the new co-ordinates of P(x, y) become (x’, y’) then the equations of transformation will be x = α + x’ cos θ – y’ sin θ and y = β + x’ sin θ + y’ cos θ.
(4) Reflection (Image of a point) :
Let (x, y) be any point, then its image with respect to
- x axis ⇒ (x, –y)
- y-axis ⇒ (–x, y)
- origin ⇒ (–x, –y)
- line y = x ⇒ (y, x)