Theoretical and Empirical Probabilities
You are already familiar with a plethora (a bunch) of information about working with probability. Let’s quickly refresh our memories:

Here are some warm-up examples:
1. At a school fair, the spinner represented in the accompanying diagram is spun twice. What is the probability that it will land in section G the first time and then in section B the second time?
Solution: The right angle tells us that sections R and G are each 1/4 of the entire circle, with section B being 1/2 of the circle.
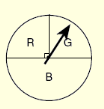
Answer: 1/4.1/2 = 1/8
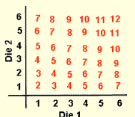
2. Shandra and Alexi roll two dice 50 times and record their results in the accompanying chart.
a.) What is their empirical probability of rolling a 7?
b.) What is the theoretical probability of rolling a 7?
c.) How do the empirical and theoretical probabilities compare?
Sum of the rolls of two dice
3, 5, 5, 4, 6, 7, 7, 5, 9, 10,
12, 9, 6, 5, 7, 8, 7, 4, 11, 6,
8, 8, 10, 6, 7, 4, 4, 5, 7, 9,
9, 7, 8, 11, 6, 5, 4, 7, 7, 4,
3, 6, 7, 7, 7, 8, 6, 7, 8, 9
Solution:
a.) Empirical probability (experimental probability or observed probability) is 13/50 = 26%.
b.) Theoretical probability (based upon what is possible when working with two dice) = 6/36 = 1/6 = 16.7% (check out the table at the right of possible sums when rolling two dice).
c.) Shandra and Alexi rolled more 7’s than would be expected theoretically.
3. The accompanying figure is a square. The interior sections are formed using congruent squares. If this figure is used as a dart board, what is the probability that the dart will hit the shaded blue region?
Solution: The large square is broken into 9 smaller congruent squares of which 5 are shaded blue. The probability is 5/9 = 55.6%.

4. Two colored dice (one red, one white) are rolled.
a.) What is the probability of rolling “box cars” (two sixes)?
b.) What is the probability of rolling “box cars” knowing the first toss is a six?
Solution:
a. The probability of getting “box cars” (two sixes) is (1/6)•(1/6) = 1/36.
b. If, however, we roll the dice and see that the white die shows a six (and the red die is out of sight), the probability of the red die being six is 1/6. The probability of rolling “box cars”, knowing that the first roll is a six, is 1/6. The probability changes when you have partial information about the situation. This is a conditional probability situation.
5. A pair of dice are rolled. What is the probability of rolling 10 or less?
Solution: The complement of rolling “10 or less” is rolling 11 or 12.
P(10 or less) = 1 – P(11 or 12) = 1 – [P(11) + P(12)] = 1 – (2/36 + 1/36) = 33/36 = 11/12
(refer to the chart in question 2 to see the number of occurrences of rolling an 11 or a 12)
