Theorems Dealing with Trapezoids
Trapezoid
Definition: A trapezoid is a quadrilateral with exactly one pair of parallel sides.
Trapezoid has only one set of parallel sides.
[The median of a trapezoid is parallel to the bases and equal to one-half the sum of the bases.]
A trapezoid has ONLY ONE set of parallel sides.
When proving a figure is a trapezoid, it is necessary to prove that two sides are parallel and two sides are NOT parallel.
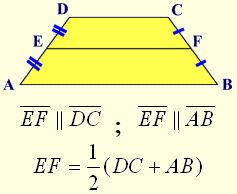 The median (also called the mid-segment) of a trapezoid is a segment that connects the midpoint of one leg to the midpoint of the other leg.
The median (also called the mid-segment) of a trapezoid is a segment that connects the midpoint of one leg to the midpoint of the other leg.
Theorem: The median (or mid-segment) of a trapezoid is parallel to each base and its length is one half the sum of the lengths of the bases.
(True for ALL trapezoids.)
Isosceles Trapezoid
Definition: An isosceles trapezoid is a trapezoid with congruent legs.

Properties:
- Isosceles Trapezoid has only one set of parallel sides
- base angles congruent
- legs congruent
- diagonals congruent
- opposite angles supplementary
Theorems:
- A trapezoid is isosceles if and only if the base angles are congruent.
- A trapezoid is isosceles if and only if the diagonals are congruent.
- If a trapezoid is isosceles, the opposite angles are supplementary.
Never assume that a trapezoid is isosceles unless you are given (or can prove) that information.
