Styles of Proof
A proof is a logical argument that establishes the truth of a statement.
Proofs are essential to mathematical inquiry. They are the means by which we can assert that we know that a mathematical concept is true. Author (and mathematician) Lewis Carroll (Alice’s Adventures in Wonderland) once said, “The charm [of mathematics] lies chiefly … in the absolute certainty of its results; for that is what, beyond all mental treasures, the human intellect craves for.”
Proving theorems is exciting, challenging and at times frustrating. The logical reasoning skills and the disciplined organization required to build a proof, enhance your critical thinking skills. In addition, you will discover one of the true (but often overlooked) beauties of mathematics – that there are often many ways to arrive at the same conclusion. Proofs are intellectual games and can actually be fun!
Presenting a proof:
Proofs are developed such that each step in the argument is in proper chronological order in relation to earlier steps. When building a proof, be sure that your argument is clearly developed and that each step is supported by a property, theorem, postulate or definition.
Remember to write a proof as if the reader knows nothing about geometry.
There are three classic styles for presenting proofs:
Method 1: The Two-Column Proof
(also called the T-Form proof or Ledger proof)
This method is most often seen in high school textbooks. Two columns are presented where the first column contains a numbered chronological list of steps (“statements”) leading to the desired conclusion. The second column contains a list of “reasons” which support each step in the proof. These reasons are properties, theorems, postulates and definitions. This method of presentation helps you to clearly display each step in your argument, and helps you to keep your ideas organized.
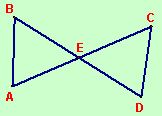 Given E is the midpoint of \(\overline { BD }\)
Given E is the midpoint of \(\overline { BD }\)
\(\overline { AE }\) ≅ \(\overline { EC }\)
Prove: ∆AEB ≅ ∆CED
Statements
- \(\overline { AE }\) ≅ \(\overline { EC }\)
- ∡BEA ≅ ∡DEC
- \(\overline { BE }\) ≅ \(\overline { ED }\)
- ∆AEB ≅ ∆CED
Reasons
- Given
- Vertical angles are congruent.
- Midpoint of a segment divides the segment into two congruent segments.
- SAS ≅ SAS
If two sides and the included angle of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent.
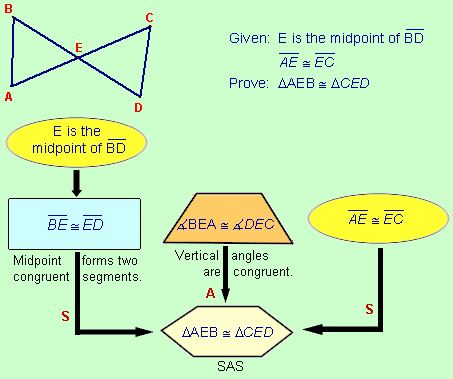
Method 2: The Flow Proof
(also called the Flowchart Proof)
This method displays the delineated structure of a proof using boxes and connecting arrows. The supporting properties, theorems, postulates and definitions are written beside the boxes. The flowchart (schematic) nature of this method resembles the logical development structure often used by computer programmers. Flow proofs can be easily adapted to both algebraic and geometric proofs. This method of presentation helps you to clearly and easily display each step in your argument.
(If you have access to the computer software Inspiration you can build flow proofs on your computer.)
Method 3: The Paragraph Proof
This is the more collegiate method of writing a proof. It consists of a detailed paragraph explaining the proof process. The paragraph is lengthy and contains steps and reasons which lead to the final conclusion. Be careful when using this method — it is easy to leave out critical steps (or supporting reasons) if you are not careful.
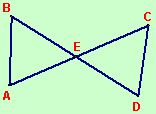 Given E is the midpoint of \(\overline { BD }\)
Given E is the midpoint of \(\overline { BD }\)
\(\overline { AE }\) ≅ \(\overline { EC }\)
Prove: ∆AEB ≅ ∆CED
We are given the figure above and the facts that E is the midpoint of \(\overline { BD }\) and that \(\overline { AE }\) ≅ \(\overline { EC }\). Since E is the midpoint of \(\overline { BD }\), we know that \(\overline { BE }\) ≅ \(\overline { ED }\) because the midpoint of a segment divides the segment into two congruent segments. Since vertical angles are congruent, ∡BEA ≅ ∡DEC. We now have sufficient information to satisfy the SAS method of proving triangles congruent. ∆AEB ≅ ∆CED because if two sides and the included angle of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent.
