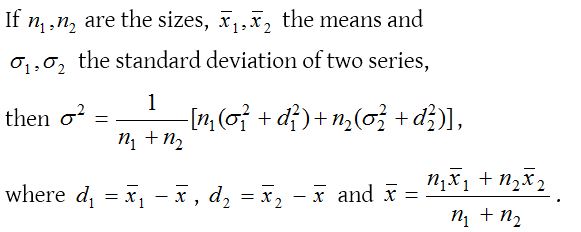Standard Deviation and Variance
Standard Deviation
Standard deviation (or S.D.) is the square root of the arithmetic mean of the square of deviations of various values from their arithmetic mean and is generally denoted by σ read as sigma. It is used in statistical analysis.
(i) Coefficient of standard deviation: To compare the dispersion of two frequency distributions the relative measure of standard deviation is computed which is known as coefficient of standard deviation and is given by
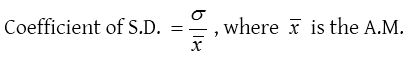
(ii) Standard deviation from individual series

(iii) Standard deviation from continuous series

Short cut method:
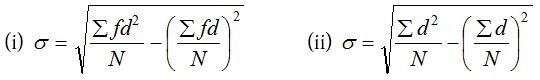
where, d = x – A = Deviation from the assumed mean A
f = Frequency of the item
N = Σf = Sum of frequencies
Example:
What is the standard deviation of the following series
| Measurements | 0-10 | 10-20 | 20-30 | 30-40 |
| Frequency | 1 | 3 | 4 | 2 |
Solution:
| Class | fi | yi | d = yi – A, A = 25 | fidi | fidi2 |
| 0-10 | 1 | 5 | – 20 | – 20 | 400 |
| 10-20 | 3 | 15 | – 10 | – 30 | 300 |
| 20-30 | 4 | 25 | 0 | 0 | 0 |
| 30-40 | 2 | 35 | 10 | 20 | 200 |
| Total | 10 | – 30 | 900 |
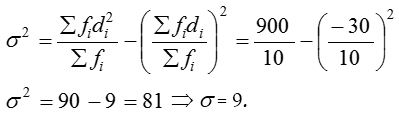
Square deviation
(i) Root mean square deviation
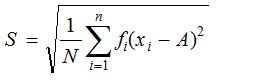
where A is any arbitrary number and S is called mean square deviation.
(ii) Relation between S.D. and root mean square deviation:
If σ be the standard deviation and S be the root mean square deviation.
Then, S2 = σ2 + d2.
Obviously, will be least when d = 0 i.e., \(\bar { x } =A\)
Hence, mean square deviation and consequently root mean square deviation is least, if the deviations are taken from the mean.
Variance
The square of standard deviation is called the variance.
Coefficient of standard deviation and variance: The coefficient of standard deviation is the ratio of the S.D. to A.M. i.e., \(\frac { \sigma }{ x }\).

Variance of the combined series: