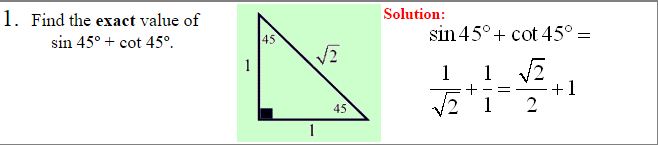
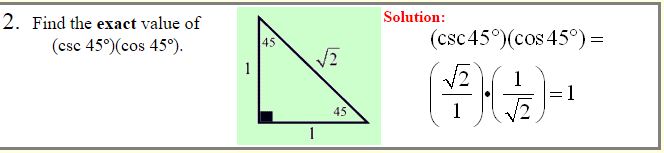
Special Right Triangle 45º- 45º- 90º
The 45º- 45º- 90º triangle is one of two special right triangles we will be investigating. The “special” nature of these triangles is their ability to yield exact answers instead of decimal approximations when dealing with trigonometric functions.
If we represent the legs of an isosceles right triangle by 1, we can use the Pythagorean Theorem to establish pattern relationships between the lengths of the legs and the hypotenuse. These relationships will be stated as “short cut formulas” that will allow us to quickly arrive at answers regarding side lengths without applying trigonometric functions, or other means.
There are two pattern formulas that apply ONLY to the 45º-45º-90º triangle.
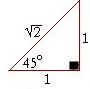
Note: the legs need not be a length of 1 for these patterns to apply.
The patterns will apply with any length legs.
45º-45º-90º (Isosceles Right Triangle)
Pattern Formulas
(you do not need to memorize these formulas as such, but you do need to memorize the patterns)
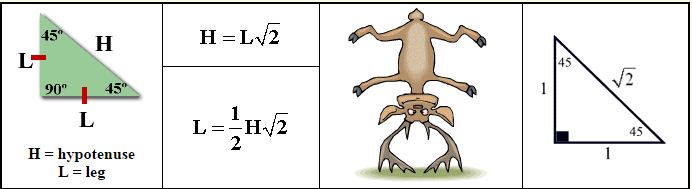
The nice thing about mathematics is that there is always another way to do the problem. If you forget these formulas, you could always use the Pythagorean Theorem or a trigonometric formula.
Let’s look at 3 solutions to this problem where you are asked to find x:
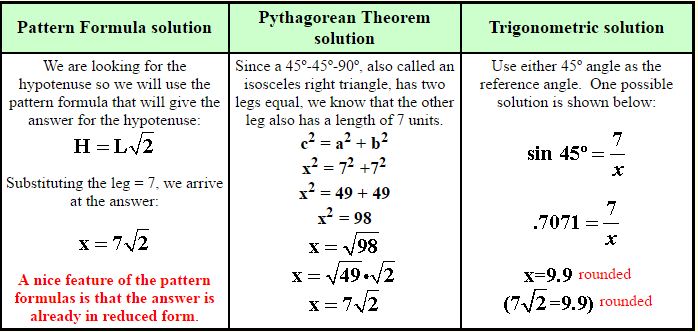
Using the newly found patterns in trig problems: