Special Right Triangle 30º- 60º- 90º
The 30º- 60º- 90º triangle is one of two special right triangles we will be investigating. The “special” nature of these triangles is their ability to yield exact answers instead of decimal approximations when dealing with trigonometric functions.

If you draw an altitude in an equilateral triangle, you will form two congruent 30º- 60º- 90º triangles. Starting with the sides of the equilateral triangle to be 2, the Pythagorean Theorem will allow us to establish pattern relationships between the sides of a 30º- 60º- 90º triangle. These relationships will be stated here as “short cut formulas” that will allow us to quickly arrive at answers regarding side lengths without applying trigonometric functions, or other means.
There are three pattern relationships that we can establish that apply ONLY to a 30º-60º-90º triangle.
Note: the hypotenuse need not be a length of 2 for these patterns to apply.
The patterns will apply with any length hypotenuse.
30º-60º-90º Triangle Pattern Formulas
(you do not need to memorize these formulas as such, but you do need to memorize the relationships)
Labeling:
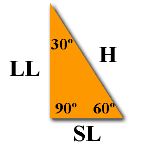
H = hypotenuse
LL = long leg (across from 60º)
SL = short leg (across from 30º)

Short Cut Pattern Formulas:
(These formulas give answers directly. We don’t need to work out the trig, as we already know the pattern relationships)

Using the patterns to find the lengths of sides:



Using the newly found patterns in trig problems:


