Solving Rational Equations
A rational equation is an equation in which one or more of the terms is a fractional one.
When solving these rational equations, we utilize one of two methods that will eliminate the denominator of each of the terms.
Method 1 :
4/x = 9/x-2
(where two fractional terms are equal to each other)
If the equation is in the form of a proportion:
a/b = c/d
you can use “product of the means = product of the extremes” or “cross-multiplication” to eliminate the denominator,
as in: a.d = b.c
Then solve the resulting equation and check.
For example: 4/x = 9/x-2

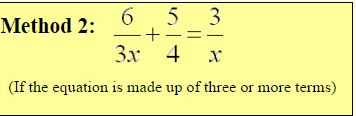
To solve the rational equation in this method, we:
(1) Identify the least common denominator (LCD),
(2) Multiply each side of the equation by the LCD, simplify, then
(3) Solve the resulting equation, and
(4) Check the answer.

The check is very important in rational equations, as you can get answers that do not check in the original equation.

