Solving Radical Equations
(This lesson will work primarily with radicals that are square roots.)
A “radical” equation is an equation in which the variable is hiding inside
a radical symbol (in the radicand).

To solve radical equations:
1. Isolate the radical (or one of the radicals) to one side of the
equal sign.
2. If the radical is a square root, square each side of the
equation. (If the radical is not a square root, raise each side to a power
equal to the index of the root.)
3. Solve the resulting equation.
4. Check your answer(s) to avoid extraneous roots.
When working with radical equations (that are square roots), …
1. you must square sides, not terms. Consider:
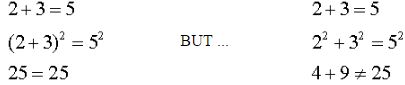
2. you must check your answers. The process of squaring the sides of an equation creates a “derived” equation which may not be equivalent to the original radical equation. Consequently, solving this new derived equation may create solutions that never previously existed. These “extra” roots that are not true solutions of the original radical equation are called extraneous roots and are rejected as answers. Consider:

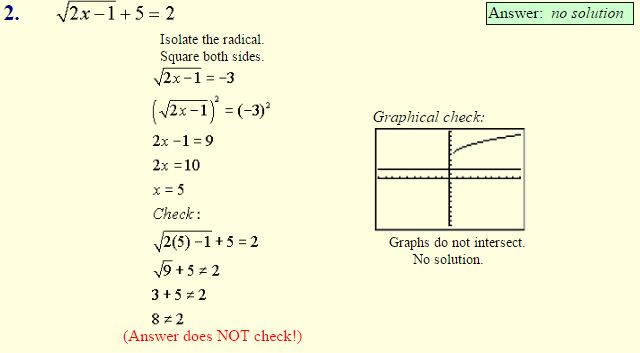
You can “see” this problem of extraneous roots by graphing. Consider
There is NO solution to this equation since the graphs do not intersect. Squaring both sides, however, creates two graphs that DO intersect which leads to a false answer.
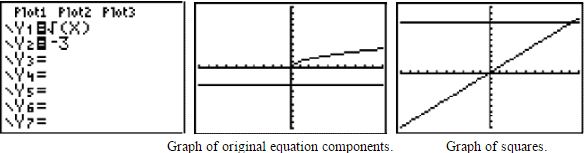
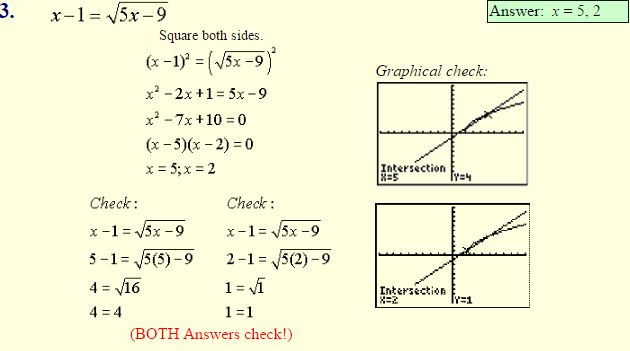
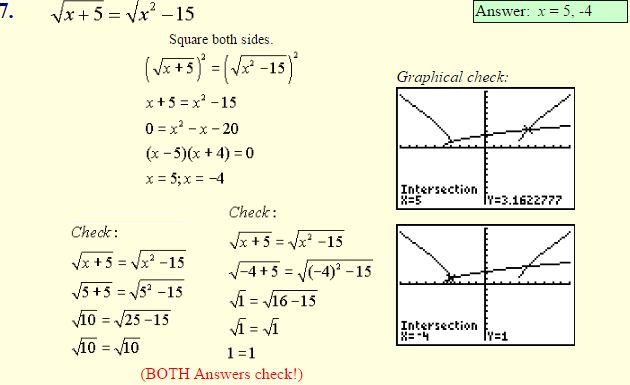
Examples: