Solving Linear Systems Algebraically Using Addition/Subtraction

Solving Linear Systems Algebraically Using Addition/Subtraction

Simultaneous equations got you baffled? Relax! You can do it!
Think of the adding or subtracting method as temporarily “eliminating” one of the variables to make your life easier.

The goal of the elimination method is to create a situation where one set of the variables will cancel each other out when the equations are added or subtracted. It may be necessary, with this method, to create coefficients for these variables that are the same (or negatives), to make the cancellation possible. This creation process is accomplished by multiplying through the equations.

Systems of Equations may also be referred to as “simultaneous equations”.
“Simultaneous” means being solved “at the same time”.

Let’s look at three examples using the “addition” or “subtraction” method for systems of equations:

1. Solve this system of equations and check: 
x + y = 12
2x – y = -6

1. First, be sure that the variables are “lined up” under one another. In this problem, they are already “lined up”.
   x + y = 12
   2x – y = -6
2. Decide which variable (“x” or “y”) will be easier to cancel (eliminate). In order for a cancellation (or elimination) to occur, the coefficients of the variables (the numbers in front of the variables) must be the same or negatives of one another. In this example, the y-values will most easily cancel out one another when the equations are added.
3. Add the equations (add the x’s, the y’s and the constants.
   Watch out for the signs. The y’s will be eliminated. Solve for x.
   
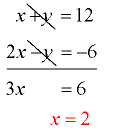
4. Substitute x = 2 into either of the ORIGINAL equations and solve for “y”. Choose the equation that will solve most easily.
   x + y = 12
   2 + y = 12
   y = 10
5.  Check: substitute x = 2 and y = 10 into BOTH ORIGINAL equations. If these answers are correct, BOTH equations will be TRUE!
   x + y = 12
   2 + 10 = 12
   12 = 12 (check)
   2x – y = -6
   2(2) – 10 = -6
   4 – 10 = -6
   -6 = -6 (check)

2. Solve this system of equations and check:
-15 – y = -7x
3x – 19 = 2y

1. Line up the variables and constants. The equations must be rearranged so this will occur.
   7x – y = 15
   3x – 2y = 19
2. Decide which variable (“x” or “y”) will be easier to cancel (eliminate). In this example, we must make adjustments so that either the x’s or y’s will cancel. If we multiply the top equation by -2, we will be able to get the y’s to cancel when we add. This is the easier method, since if we wanted the x’s to cancel we would need to multiply both equations (by 3 and by -7, for example).
   Yes, you could also multiply by +2 and then “subtract” the equations.
   -2(7x – y = 15)
   3x – 2y = 19
   -14x + 2y = -30
   3x – 2y = 19
3. Add the equations (add the x’s, the y’s and the constants).
   Watch out for the signs. The y’s will be eliminated. Solve for x
   
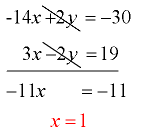
4. Substitute x = 1 into either of the ORIGINAL equations and
   solve for “y”. Choose the equation that will solve most easily.
   3x – 2y = 19
   3(1)- 2y = 19
   3 – 2y = 19
   -2y = 16
   y = -8
5. Check: substitute x = 1 and y = -8 into BOTH ORIGINAL equations. If these answers are correct, BOTH equations will be TRUE!
   7x – y = 15
   7(1) – (-8) = 15
   7 + 8 = 15
   15 = 15 (check)
   3x – 2y = 19
   3(1) – 2(-8) = 19
   3 + 16 = 19
   19 = 19 (check)