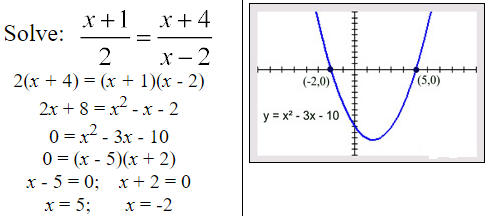Solving Factorable Quadratic Equations
A quadratic equation is a polynomial equation of degree two. The standard form is ax² + bx + c = 0.

There’s no magic to solving quadratic equations. Quadratic equations can be solved by factoring and also by graphing.
The factoring method of solution:
Let’s do a quick review of factoring.
Factoring Method:
- Express the equation in the form ax2 + bx + c = 0.
- Factor the left hand side (if 0 is on the right).
- Set each of the two factors equal to zero.
- Solve for x to determine the roots (or zeros).
Simple quadratic equations with rational roots can be solved by factoring.
If you can factor, you will be able to solve factorable quadratic equations.
Examples of Solving Quadratic Equations by Factoring:
Example 1:
Factoring with GCF
(greatest common factor):
Find the largest value which can be factored from each term on the left side of the quadratic equation.
The roots (zeros) correspond to the locations of the x-intercepts of the function y = 4x2 – 28x.
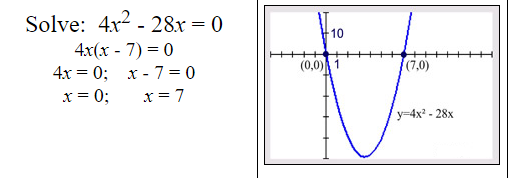
Example 2:
Factoring Trinomial with Leading Coefficient of One:
When the leading coefficient is one, the product of the roots will be the constant term, and the sum of the roots will be the coefficient of the middle x-term.
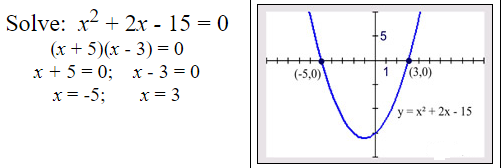
Example 3:
Factoring Difference of Two Squares:
Remember the pattern for the difference of two squares, where the factors are identical except for the sign between the terms.
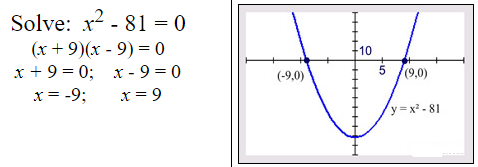
Example 4:
Factoring Trinomial with Leading Coefficient Not One:
Life gets more difficult when the leading coefficient is not one.
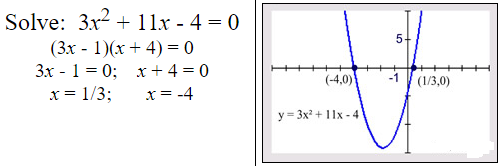
Example 5:
Where’s the x2 ?
Sometimes you have to “work” on the equation to get the needed quadratic form. In this case, distribute, and the x2 will appear.
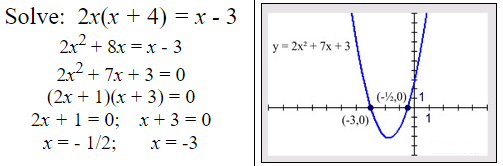
Example 6:
Dealing with Proportions:
x2 may appear when cross multiplying (“product of the means equals product of the extremes”) is employed in a proportion.