Solving Equations
Solving linear equations is just a matter of undoing operations that are being done to the variable. The task is always to isolate the variable — get the variable ALONE on one side of the equal sign.
Remember when solving equations to “keep the equation balanced” by making the same changes to BOTH sides of the equal sign.
Example 1: In a simple equation, you may only have to undo one operation to solve the equation.
Solve this equation for x: x + 3 = 8
The variable is x and we need to get it alone.
In the problem, 3 is being added to the variable, so to get rid of the added 3, we do the opposite —- subtract 3.
We are actually employing the additive inverse property to create a 0 since +3 – 3 = 0. Then the additive identity is used to get x alone since x + 0 = x.
(Remember to subtract 3 from both sides of the equation to “keep the equation balanced”.)
Check your answer:
You will always know if your answer is correct by doing a simple “check” — substitute your answer into the original equation and see if the result is true.
Check:
x + 3 = 8
5 + 3 = 8
8 = 8 true
Example 2: In an equation which has more than one operation, we have to undo the operations in the correct order. First, undo addition or subtraction, then undo multiplication or division.
Solve this equation for x: 5x – 2 = 13
The variable is x.
The question is multiplying x by 5, and then subtracting 2.
First, undo the subtraction by adding 2.
Then, undo the multiplication by dividing by 5.
This process is actually employing the multiplicative inverse to create the value of 1 and then employing the multiplicative identity to isolate the x.
(Remember to perform your changes to both sides of the equation to “keep the equation balanced”.)
Check your answer:
5x – 2 = 13
5(3) – 2 = 13
15 – 2 = 13
13 = 13 true
Example 3: Suppose there are variables on both sides of the equation. The trick now, is to get the variables on the same side by adding them or subtracting them.
Solve for x: 4x + 5 = x – 4
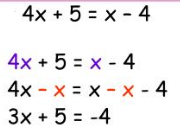
Hint: Some students think of “moving” one variable to the other side of the equal sign as “moving” the variable over the “equal sign bridge”. Moving any term across the “equal sign bridge” changes the term’s sign (like paying a toll).
4x + 5 = x – 4
4x – x + 5 = -4 as the x moves to the left over the “equal sign bridge”, it changes its sign to negative.
Example 4: Sometimes there are equations which have multiple terms on the same side. The trick here is to combine all the similar terms before solving.
Solve for x: 6x + 8 = x – 12
This equation has variables on both sides of the equal sign. We need to get the x’s combined into one term.
“Move” the variable with the smaller coefficient (in this case the x term on the right). The sign in front of this x-term is implied to be positive.
Subtract x from both sides.
Now, proceed as shown in the examples above.
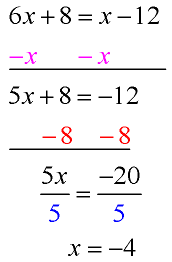
Check answer:
Check:
6x + 8 = x – 12
6(-4) + 8 = (-4) – 12
-24 + 8 = -4 – 12
-16 = -16 True!
Example 5: There are also equations with parentheses. The first step in these problems is to multiply and get rid of the parentheses.
Solve for m: 2(m + 10) = 4(m – 15)
This equation contains parentheses.
The first step is to distribute across the parentheses to get rid of the parentheses. (Multiply through.)
Now, proceed as shown in the examples above.
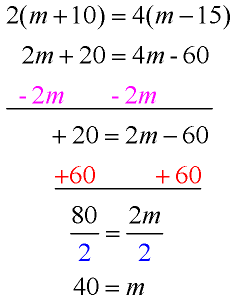
Check answer:
Check:
2(m + 10) = 4(m – 15)
2(40 + 10) =4(40 – 15)
2(50) = 4(25)
100 = 100 True!
Example 6: The last type of equation contains decimals.
Solve for x: 4x + 2.6 = 3x + 8.1
Equations may contain decimals as constants (as seen here) or as coefficients.
There is no secret to solving problems with decimals. Simply solve as you would solve an equation with integer values.
Proceed as shown in the examples above.
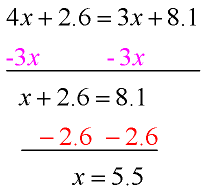
Check answer:
Check:
4x + 2.6 = 3x + 8.1
4(5.5) + 2.6 =3(5.5) + 8.1
22 + 2.6 =16.5 + 8.1
24.6 = 24.6 True!