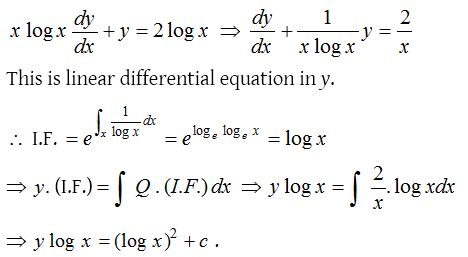A Plus Topper

Improve your Grades

Solution of First Order Linear Differential Equations

by

Solution of First Order Linear Differential Equations

Linear and non-linear differential equations

A differential equation is a linear differential equation if it is expressible in the form
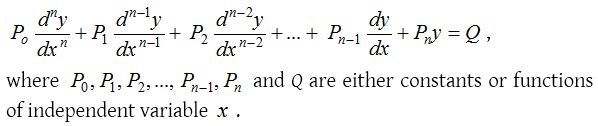
Solution of First Order Linear Differential Equations 1
Thus, if a differential equation when expressed in the form of a polynomial involves the derivatives and dependent variable in the first power and there are no product of these, and also the coefficient of the various terms are either constants or functions of the independent variable, then it is said to be linear differential equation. Otherwise, it is a non linear differential equation.
It follows from the above definition that a differential equation will be non-linear differential equation if

  1. its degree is more than one
  2. any of the differential coefficient has exponent more than one.
  3. exponent of the dependent variable is more than one.
  4. products containing dependent variable and its differential coefficients are present.

Linear differential equation of first order

The general form of a linear differential equation of first order is
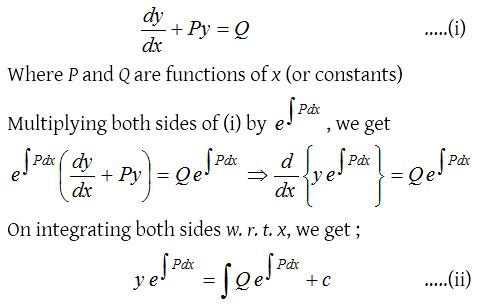
Solution of First Order Linear Differential Equations 2
which is the required solution, where c is the constant of integration. e∫P dx is called the integrating factor. The solution (ii) in short may also be written as y.(I.F) = ∫Q.(I.F) dx + c.

Linear differential equations of the form \(\frac { dy }{ dx } +Rx=S\)

Sometimes a linear differential equation can be put in the form \(\frac { dy }{ dx } +Rx=S\) where R and S are functions of y or constants. Note that y is independent variable and x is a dependent variable.

Equations reducible to linear form (Bernoulli’s differential equation)

The differential equation of type \(\frac { dy }{ dx } +Py=Q{ y }^{ n }\)  …..(i)
Where P and Q are constants or functions of x alone and n is a constant other than zero or unity, can be reduced to the linear form by dividing by yn and then putting y-n+1 = v, as explained below.
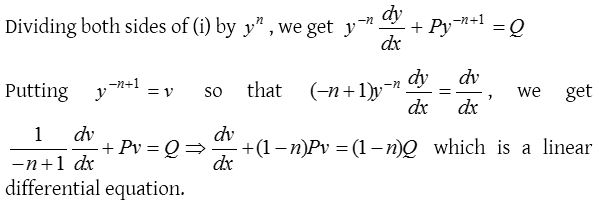
Solution of First Order Linear Differential Equations 3
Note : If n = 1, then we find that the variables in equation (i) are separable and it can be easily integrated by the method discussed in variable separable from.

Differential equation of the form \(\frac { dy }{ dx } +P\phi (y)=Q\psi (y)\)

\(\frac { dy }{ dx } +P\phi (y)=Q\psi (y)\), where P and Q are functions of x alone or constants.
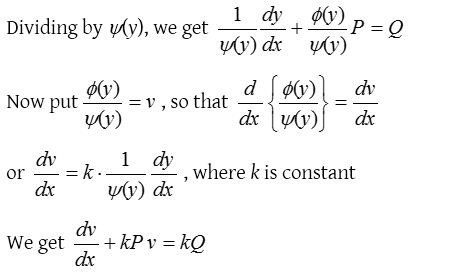
Solution of First Order Linear Differential Equations 4
Which is linear differential equation.

Linear Differential Equations Problems with Solutions

1.
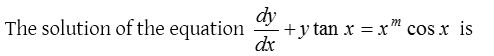
Solution of First Order Linear Differential Equations 5
Solution:
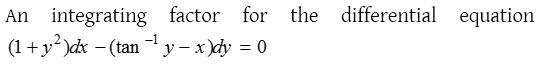
Solution of First Order Linear Differential Equations 6
2.
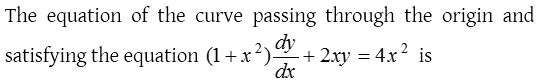
Solution of First Order Linear Differential Equations 7
Solution:
Solution of First Order Linear Differential Equations 8
3.
Solution of First Order Linear Differential Equations 9
Solution:
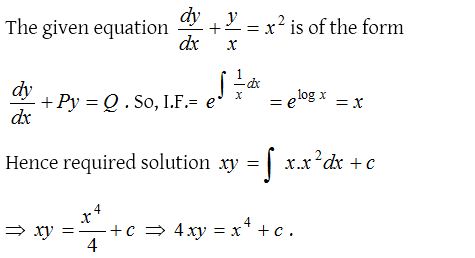
Solution of First Order Linear Differential Equations 10
4.
Solution of First Order Linear Differential Equations 11
Solution:
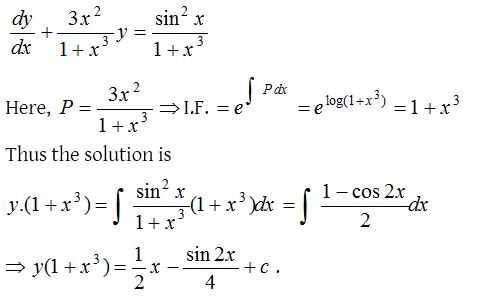
Solution of First Order Linear Differential Equations 12
5.
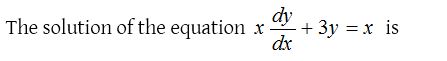
Solution of First Order Linear Differential Equations 13
Solution:
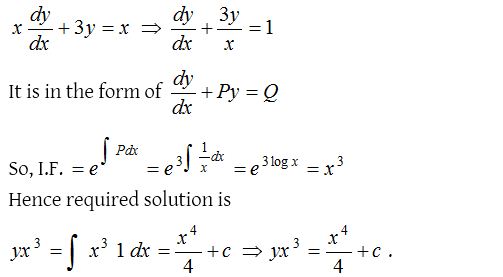
Solution of First Order Linear Differential Equations 14
6.
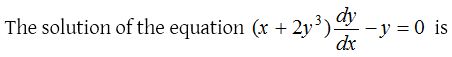
Solution of First Order Linear Differential Equations 15
Solution:
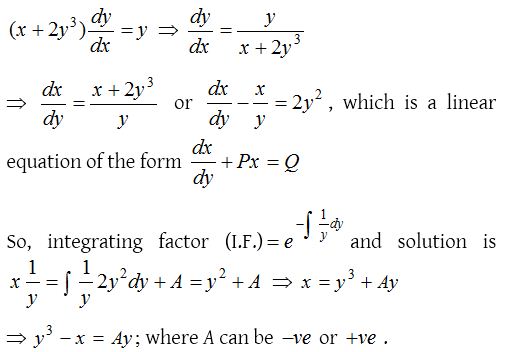
Solution of First Order Linear Differential Equations 16
7.
Solution of First Order Linear Differential Equations 17
Solution:
Solution of First Order Linear Differential Equations 18
8.
Solution of First Order Linear Differential Equations 19
Solution:
Solution of First Order Linear Differential Equations 20


Equations reducible to linear form (Bernoulli's differential equation) Linear and non-linear differential equations Linear differential equation of first order Linear Differential Equations Problems with Solutions