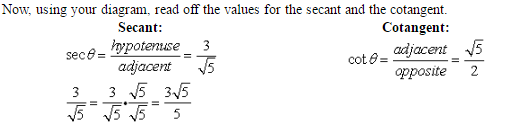The Six Trigonometric Functions and Reciprocals Functions
In a right triangle, there are actually six possible trigonometric ratios, or functions.
A Greek letter (such as theta or phi ) will now be used to represent the angle.
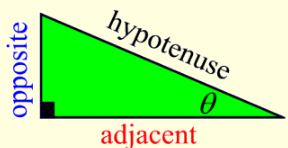
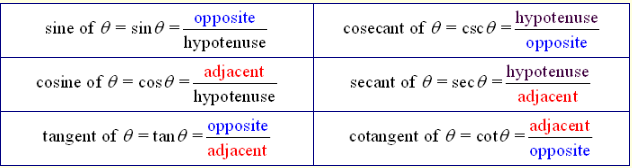
Notice that the three new ratios at the right are reciprocals of the ratios on the left.
Applying a little algebra shows the connection between these functions.



Examples:
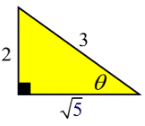
1. Given the triangle at the right, express the exact value of the six trig functions in relation to theta.
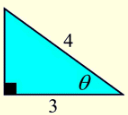
Solution: Find the missing side of the right triangle using the Pythagorean Theorem. Then, using the diagram, express each function as a ratio of the lengths of the sides. Do not “estimate” the answers.

The following examples pertain to a right triangle in Quadrant I:

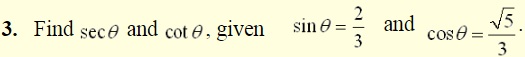
Since sine is opposite over hypotenuse, position the 2 and the 3 accordingly in relation to the angle theta. Now, since cosine is adjacent over hypotenuse, position these values (the 3 should already be properly placed). Be sure that the largest value is on the hypotenuse and that the Pythagorean Theorem is true for these values. (If you are not given the third side, use the Pythagorean Theorem to find it.)