Simplifying Radicals
(For this lesson, the term “radical” will refer only to “square root”.)
When working with the simplification of radicals you must remember some basic information about perfect square numbers.
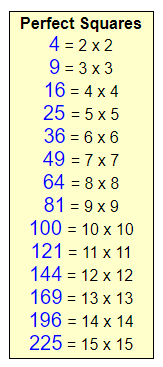 While there are certainly many more perfect squares, the ones appearing in the charts above are the ones most commonly used.
While there are certainly many more perfect squares, the ones appearing in the charts above are the ones most commonly used.
To simplify means to find another expression with the same value. It does not mean to find a decimal approximation.
To simplify (or reduce) a radical:
- Find the largest perfect square which will divide evenly into the number under your radical sign. This means that when you divide, you get no remainders, no decimals, no fractions.
Reduce: √48 the largest perfect square that divides evenly into 48 is 16.
If the number under your radical cannot be divided evenly by any of the perfect squares, your radical is already in simplest form and cannot be reduced further. - Write the number appearing under your radical as the product (multiplication) of the perfect square and your answer from dividing.
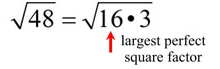
- Give each number in the product its own radical sign.
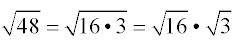
- Reduce the “perfect” radical which you have now created.
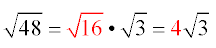
- You now have your answer.
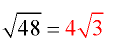
What happens if I do not choose the largest perfect square to start the process?
If instead of choosing 16 as the largest perfect square to start this process, you choose 4, look what happens…..
![]()
Unfortunately, this answer is not in simplest form.
The 12 can also be divided by the perfect square (4).
![]()
If you do not choose the largest perfect square to start the process, you will have to repeat the process.
Example: Simplify √23
The number 23 cannot be factored by any of the perfect squares (23 is prime). This is a trick question as it is already in simplest form and cannot be reduced further.
Example: Simplify √13
1. Give the numerator and denominator their own radical signs.
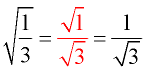
2. Multiply the numerator and denominator by a radical that will get rid of the radical in the denominator, by creating a perfect square under the radical. If a smaller value cannot be found, multiply by the same radical value that is in the denominator, automatically creating a perfect square.
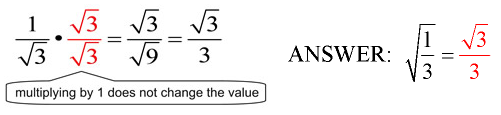
This process of removing a radical from the denominator is referred to as “rationalizing the denominator” because it turns the denominator into a rational (not irrational) value.
Example: Simplify 6√72
![]()
Note: The examples shown in these lessons on radicals show ALL of the steps in the process. It may NOT be necessary for you to list EVERY step. As long as you understand the process and can arrive at the correct answer, you are ALL SET!!
