Sets and Venn Diagrams

Set: A set is well defined class or collection of objects.
Sets and Venn Diagrams 1

Venn-Euler diagrams

The combination of rectangles and circles are called Venn-Euler diagrams or simply Venn-diagrams.
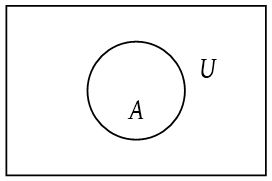Sets and Venn Diagrams 2 If A and B are not equal but they have some common elements, then to represent A and B we draw two intersecting circles. Two disjoints sets are represented by two non-intersecting circles.

Operations on sets

Union of sets: Let A and B be two sets. The union of A and B is the set of all elements which are in set A or in B. We denote the union of A and B by A∪B, which is usually read as “A union B”.
Symbolically, A ∪ B = {x : x ∈ A or x ∈ B}
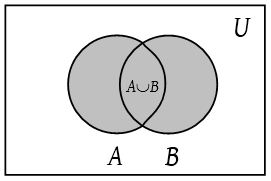
Intersection of sets: Let A and B be two sets. The intersection of A and B is the set of all those elements that belong to both A and B.
The intersection of A and B is denoted by A ∩ B (read as “A intersection B”).
Thus, A ∩ B = {x : x ∈ A and x ∈ B}.
Disjoint sets: Two sets A and B are said to be disjoint, if A∩B = ϕ. If A∩B ≠ ϕ, then A and B are said to be non-intersecting or non-overlapping sets.
Example: Sets {1, 2}; {3, 4} are disjoint sets.
Difference of sets: Let A and B be two sets. The difference of A and B written as A – B, is the set of all those elements of A which do not belong to B.

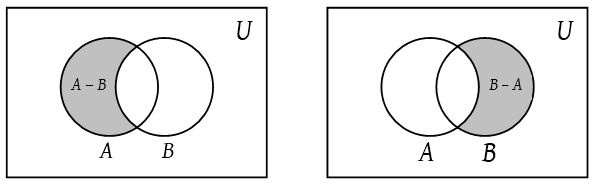
Thus, A – B = {x : x ∈ A and x ∉ B}
Similarly, the difference B – A is the set of all those elements of B that do not belong to A i.e., B – A = {x ∈ B : and x ∉ A}.
Example: Consider the sets A = {1, 2, 3} and B = {3, 4, 5} then A – B = {1, 2} and B – A = {4, 5}.
Symmetric difference of two sets: Let A and B be two sets. The symmetric difference of sets A and B is the set (A – B) ∪ (B – A) and is denoted by A ∆ B. Thus, A ∆ B = (A – B) ∪ (B – A) = {x : x ∉ A∩B}.
Complement of a set: Let U be the universal set and let A be a set such that A ⊂ U. Then, the complement of A with respect to U is denoted by A‘ or A^c or C(A) or U – A and is defined the set of all those elements of U which are not in A.

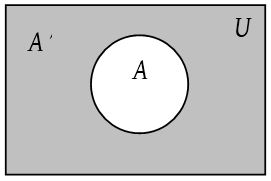
Thus, A‘ = {x ∈ U : x ∉ A}.
Clearly, x ∈ A‘ ⇔ x ∉ A
Example : Consider U = {1, 2, …… 10}
and A = {1, 3, 5, 7, 9}.
Then A‘ = {2, 4, 6, 8, 10}

https://www.youtube.com/watch?v=_YpK82_mjns

Some important results on number of elements in sets

If A, B and C are finite sets and U be the finite universal set, then

n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
n(A ∪ B) = n(A) + n(B) ⇔ A, B are disjoint non-void sets.
n(A – B) = n(A) – n(A ∩ B) i.e., n(A – B) + n(A ∩ B) = n(A)
n(A ∆ B) = Number of elements which belong to exactly one of A or B = n((A – B) ∪ (B – A)) = n (A – B) + n(B – A) [∵ (A – B) and (B – A) are disjoint]
= n(A) – n(A ∩ B) + n(B) – n(A ∩ B) = n(A) + n(B) – 2n(A ∩ B)
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ B ∩ C)
n (Number of elements in exactly two of the sets A, B, C) = n(A ∩ B) + n(B ∩ C) + n(C ∩ A) – 3n(A ∩ B ∩ C)
n(Number of elements in exactly one of the sets A, B, C) = n(A) + n(B) + n(C) – 2n(A ∩ B) – 2n(B ∩ C) – 2n(A∩ C) + 3n(A ∩ B ∩ C)
n(A‘ ∪ B‘) = n(A ∩ B)‘ = n(U) – n(A ∩ B)
n(A‘ ∩ B‘) = n(A ∪ B)‘ = n(U) – n(A ∪ B)

Laws of algebra of sets

(1) Idempotent laws: For any set A, we have

A ∪ A = A
A ∩ A = A

(2) Identity laws: For any set A, we have

A ∪ ϕ = A
A ∩ U = A
i.e., ϕ and U are identity elements for union and intersection respectively.

(3) Commutative laws: For any two sets A and B, we have

A ∪ B = B ∪ A
A ∩ B = B ∩ A
A ∆ B = B ∆ A
i.e., union, intersection and symmetric difference of two sets are commutative.
(A – B) ≠ (B – A)
(A × B) ≠ (B × A)
i.e., difference and cartesian product of two sets are not commutative

(4) Associative laws: If A, B and C are any three sets, then

(A ∪ B) ∪ C = A ∪ (B ∪ C)
A ∩ (B ∩ C) = (A ∩ B) ∩ C
(A ∆ B)∆C = A∆(B ∆ C)
i.e., union, intersection and symmetric difference of two sets are associative.
(A – B) – C ≠ A – (B – C)
(A × B) × C ≠ A × (B × C)
i.e., difference and cartesian product of two sets are not associative.

(5) Distributive law: If A, B and C are any three sets, then

A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
i.e., union and intersection are distributive over intersection and union respectively.
A × (B ∩ C) = (A × B) ∩ (A × C)
A × (B ∪ C) = (A × B) ∪ (A × C)
A × (B – C) = (A × B) – (A × C)

(6) De-Morgan’s law: If A, B and C are any three sets, then