Selina Concise Mathematics Class 10 ICSE Solutions Remainder and Factor Theorems

Selina Concise Mathematics Class 10 ICSE Solutions Remainder and Factor Theorems

Selina Publishers Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems

Remainder and Factor Theorems Exercise 8A – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.

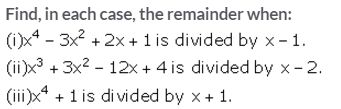
Solution:
By remainder theorem we know that when a polynomial f (x) is divided by x – a, then the remainder is f(a).

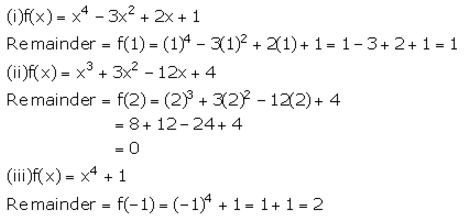
Question 2.

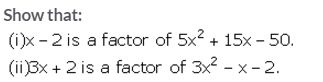
Solution:
(x – a) is a factor of a polynomial f(x) if the remainder, when f(x) is divided by (x – a), is 0, i.e., if f(a) = 0.

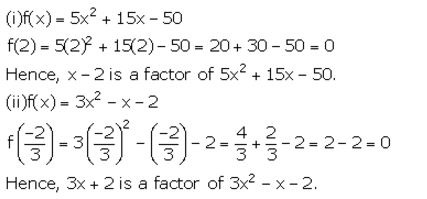
Question 3.
Use the Remainder Theorem to find which of the following is a factor of 2x³ + 3x² – 5x – 6.
(i) x + 1
(ii) 2x – 1
(iii) x + 2
Solution:
By remainder theorem we know that when a polynomial f (x) is divided by x – a, then the remainder is f(a).
Let f(x) = 2x³ + 3x² – 5x – 6
(i) f (-1) = 2(-1)³ + 3(-1)² – 5(-1) – 6 = -2 + 3 + 5 – 6 = 0
Thus, (x + 1) is a factor of the polynomial f(x).

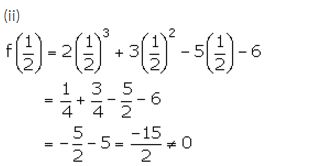
Thus, (2x – 1) is not a factor of the polynomial f(x).
(iii) f (-2) = 2(-2)³ + 3(-2)² – 5(-2) – 6 = -16 + 12 + 10 – 6 = 0
Thus, (x + 2) is a factor of the polynomial f(x).

Question 4.
(i) If 2x + 1 is a factor of 2x² + ax – 3, find the value of a.
(ii) Find the value of k, if 3x – 4 is a factor of expression 3x² + 2x – k.
Solution:

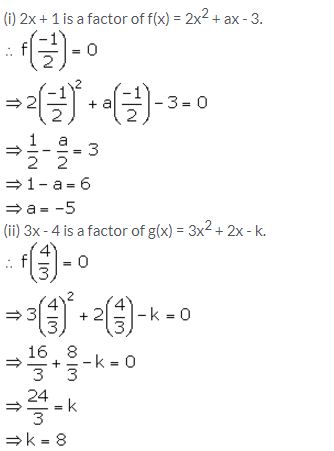
Question 5.
Find the values of constants a and b when x – 2 and x + 3 both are the factors of expression x³ + ax² + bx – 12.
Solution:

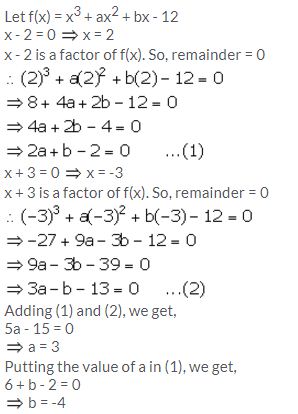
Question 6.
find the value of k, if 2x + 1 is a factor of (3k + 2)x³ + (k – 1).
Solution:

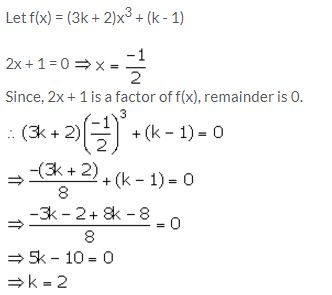
Question 7.
Find the value of a, if x – 2 is a factor of 2x⁵ – 6x⁴ – 2ax³ + 6ax² + 4ax + 8.
Solution:
f(x) = 2x⁵ – 6x⁴ – 2ax³ + 6ax² + 4ax + 8
x – 2 = 0 ⇒  x = 2
Since, x – 2 is a factor of f(x), remainder = 0.
2(2)⁵ – 6(2)⁴ – 2a(2)³ + 6a(2)² + 4a(2) + 8 = 0
64 – 96 – 16a + 24a + 8a + 8 = 0
-24 + 16a = 0
16a = 24
a = 1.5

Question 8.
Find the values of m and n so that x – 1 and x + 2 both are factors of x³ + (3m + 1) x² + nx – 18.
Solution:

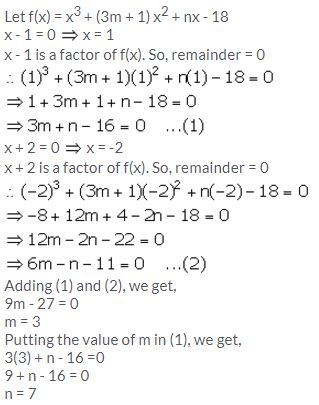
Question 9.
When x³ + 2x² – kx + 4 is divided by x – 2, the remainder is k. Find the value of constant k.
Solution:

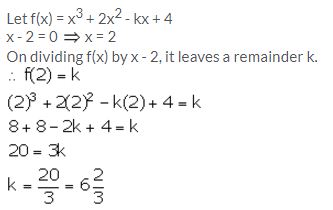
Question 10.
Find the value of a, if the division of ax³ + 9x² + 4x – 10 by x + 3 leaves a remainder 5.
Solution:

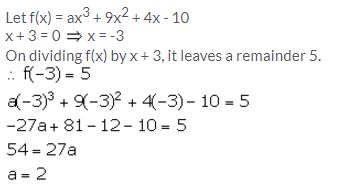
Question 11.
If x³ + ax² + bx + 6 has x – 2 as a factor and leaves a remainder 3 when divided by x – 3, find the values of a and b.
Solution:

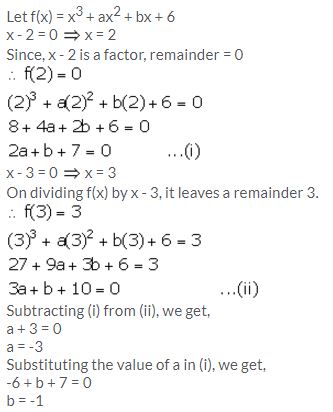
Question 12.
The expression 2x³ + ax² + bx – 2 leaves remainder 7 and 0 when divided by 2x – 3 and x + 2 respectively. Calculate the values of a and b.
Solution:

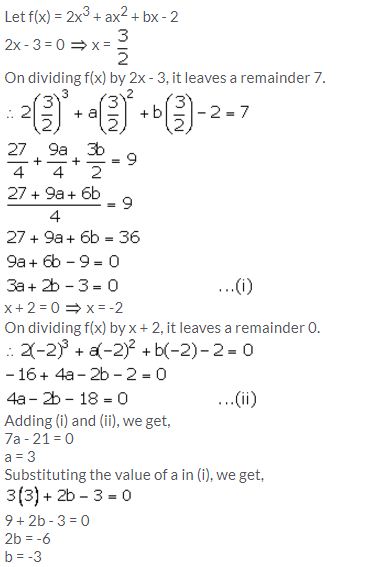
Question 13.
What number should be added to 3x³ – 5x² + 6x so that when resulting polynomial is divided by x – 3, the remainder is 8?
Solution:

Question 14.
What number should be subtracted from x³ + 3x² – 8x + 14 so that on dividing it with x – 2, the remainder is 10.
Solution:

Question 15.
The polynomials 2x³ – 7x² + ax – 6 and x³ – 8x² + (2a + 1)x – 16 leaves the same remainder when divided by x – 2. Find the value of ‘a’.
Solution:

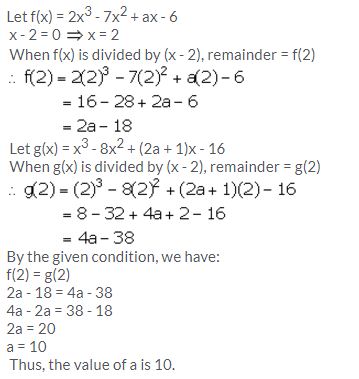
Question 16.
If (x – 2) is a factor of the expression 2x³ + ax² + bx – 14 and when the expression is divided by (x – 3), it leaves a remainder 52, find the values of a and b
Solution:

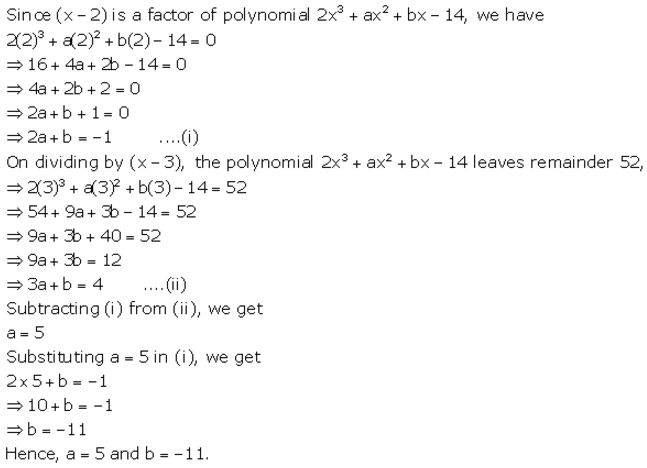
Question 17.
Find ‘a‘ if the two polynomials ax³ + 3x² – 9 and 2x³ + 4x + a, leave the same remainder when divided by x + 3.
Solution:

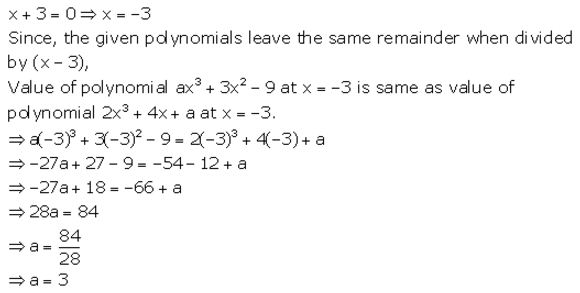
Remainder and Factor Theorems Exercise 8B – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
Using the Factor Theorem, show that:
(i) (x – 2) is a factor of x³ – 2x² – 9x + 18. Hence, factorise the expression x³ – 2x² – 9x + 18 completely.
(ii) (x + 5) is a factor of 2x³ + 5x² – 28x – 15. Hence, factorise the expression 2x³ + 5x² – 28x – 15 completely.
(iii) (3x + 2) is a factor of 3x³ + 2x² – 3x – 2. Hence, factorise the expression 3x³ + 2x² – 3x – 2 completely.
Solution:

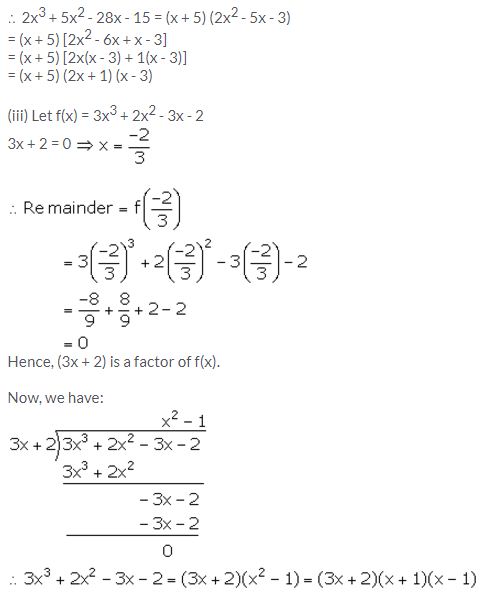
Question 2.
Using the Remainder Theorem, factorise each of the following completely.
(i) 3x³ + 2x² − 19x + 6
(ii) 2x³ + x² – 13x + 6
(iii) 3x³ + 2x² – 23x – 30
(iv) 4x³ + 7x² – 36x – 63
(v) x³ + x² – 4x – 4
Solution:

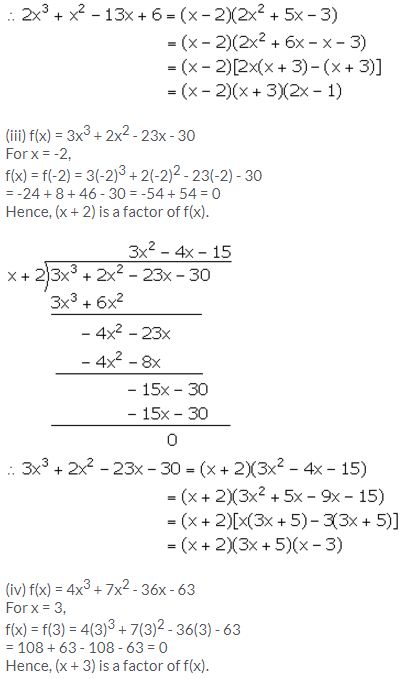
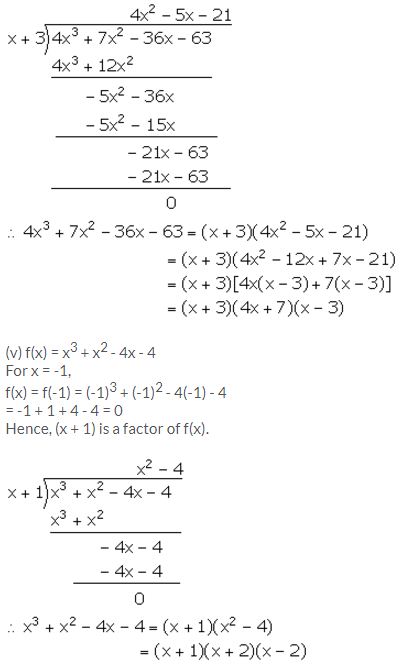
Question 3.
Using the Remainder Theorem, factorise the expression 3x³ + 10x² + x – 6. Hence, solve the equation 3x³ + 10x² + x – 6 = 0.
Solution:

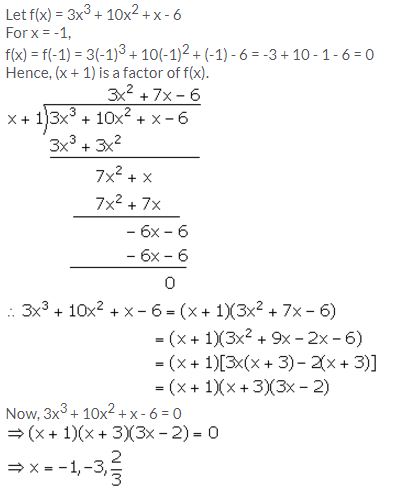
Question 4.
Factorise the expression f (x) = 2x³ – 7x² – 3x + 18. Hence, find all possible values of x for which f(x) = 0.
Solution:

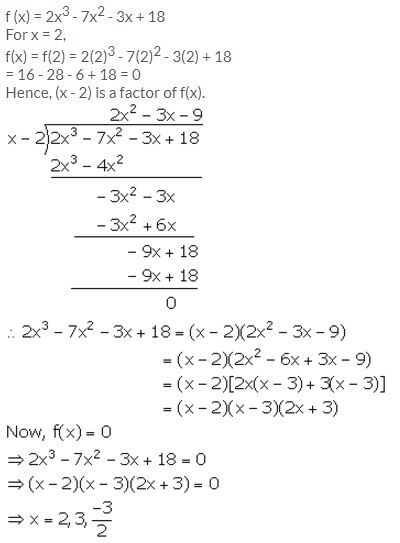
Question 5.
Given that x – 2 and x + 1 are factors of f(x) = x³ + 3x² + ax + b; calculate the values of a and b. Hence, find all the factors of f(x).
Solution:

Question 6.
The expression 4x³ – bx² + x – c leaves remainders 0 and 30 when divided by x + 1 and 2x – 3 respectively. Calculate the values of b and c. Hence, factorise the expression completely.
Solution:

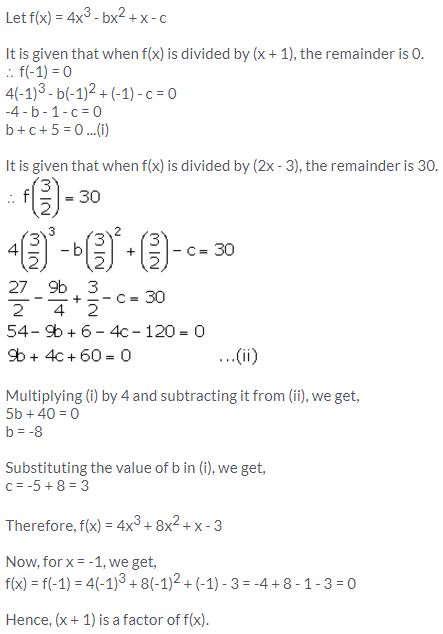
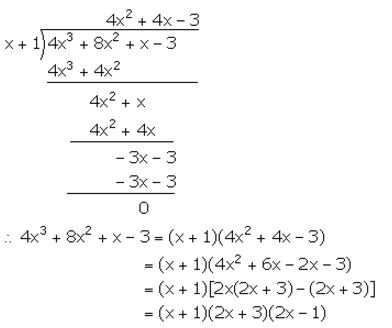
Question 7.
If x + a is a common factor of expressions f(x) = x² + px + q and g(x) = x² + mx + n;

Solution:

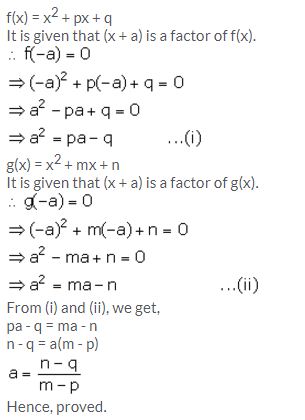
Question 8.
The polynomials ax³ + 3x² – 3 and 2x³ – 5x + a, when divided by x – 4, leave the same remainder in each case. Find the value of a.
Solution:
Let f(x) = ax³ + 3x² – 3
When f(x) is divided by (x – 4), remainder = f(4)
f(4) = a(4)³ + 3(4)² – 3 = 64a + 45
Let g(x) = 2x³ – 5x + a
When g(x) is divided by (x – 4), remainder = g(4)
g(4) = 2(4)³ – 5(4) + a = a + 108
It is given that f(4) = g(4)
64a + 45 = a + 108
63a = 63
a = 1

Question 9.
Find the value of ‘a’, if (x – a) is a factor of x³ – ax² + x + 2.
Solution:
Let f(x) = x³ – ax² + x + 2
It is given that (x – a) is a factor of f(x).
Remainder = f(a) = 0
a³ – a³ + a + 2 = 0
a + 2 = 0
a = -2

Question 10.
Find the number that must be subtracted from the polynomial 3y³ + y² – 22y + 15, so that the resulting polynomial is completely divisible by y + 3.
Solution:
Let the number to be subtracted from the given polynomial be k.
Let f(y) = 3y³ + y² – 22y + 15 – k
It is given that f(y) is divisible by (y + 3).
Remainder = f(-3) = 0
3(-3)³ + (-3)² – 22(-3) + 15 – k = 0
-81 + 9 + 66 + 15 – k = 0
9 – k = 0
k = 9

Remainder and Factor Theorems Exercise 8C – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
Show that (x – 1) is a factor of x³ – 7x² + 14x – 8. Hence, completely factorise the given expression.
Solution:

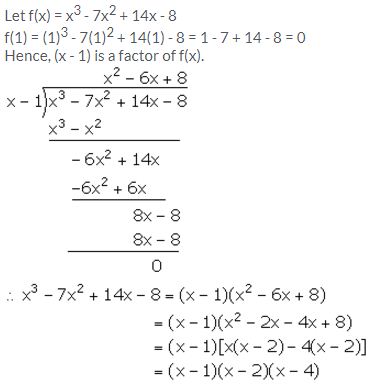
Question 2.
Using Remainder Theorem, factorise:
x³ + 10x² – 37x + 26 completely.
Solution:

Question 3.
When x³ + 3x² – mx + 4 is divided by x – 2, the remainder is m + 3. Find the value of m.
Solution:
Let f(x) = x³ + 3x² – mx + 4
According to the given information,
f(2) = m + 3
(2)³ + 3(2)² – m(2) + 4 = m + 3
8 + 12 – 2m + 4 = m + 3
24 – 3 = m + 2m
3m = 21
m = 7

Question 4.
What should be subtracted from 3x³ – 8x² + 4x – 3, so that the resulting expression has x + 2 as a factor?
Solution:
Let the required number be k.
Let f(x) = 3x³ – 8x² + 4x – 3 – k
According to the given information,
f (-2) = 0
3(-2)³ – 8(-2)² + 4(-2) – 3 – k = 0
-24 – 32 – 8 – 3 – k = 0
-67 – k = 0
k = -67
Thus, the required number is -67.

Question 5.
If (x + 1) and (x – 2) are factors of x³ + (a + 1)x² – (b – 2)x – 6, find the values of a and b. And then, factorise the given expression completely.
Solution:
Let f(x) = x³ + (a + 1)x² – (b – 2)x – 6
Since, (x + 1) is a factor of f(x).
Remainder = f(-1) = 0
(-1)³ + (a + 1)(-1)² – (b – 2) (-1) – 6 = 0
-1 + (a + 1) + (b – 2) – 6 = 0
a + b – 8 = 0 …(i)
Since, (x – 2) is a factor of f(x).
Remainder = f(2) = 0
(2)³ + (a + 1) (2)² – (b – 2) (2) – 6 = 0
8 + 4a + 4 – 2b + 4 – 6 = 0
4a – 2b + 10 = 0
2a – b + 5 = 0 …(ii)
Adding (i) and (ii), we get,
3a – 3 = 0
a = 1
Substituting the value of a in (i), we get,
1 + b – 8 = 0
b = 7
f(x) = x³ + 2x² – 5x – 6
Now, (x + 1) and (x – 2) are factors of f(x). Hence, (x + 1) (x – 2) = x² – x – 2 is a factor of f(x).

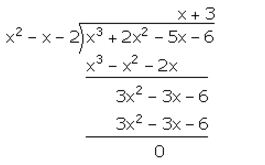
f(x) = x³ + 2x² – 5x – 6 = (x + 1) (x – 2) (x + 3)

Question 6.
If x – 2 is a factor of x² + ax + b and a + b = 1, find the values of a and b.
Solution:
Let f(x) = x² + ax + b
Since, (x – 2) is a factor of f(x).
Remainder = f(2) = 0
(2)² + a(2) + b = 0
4 + 2a + b = 0
2a + b = -4 …(i)
It is given that:
a + b = 1 …(ii)
Subtracting (ii) from (i), we get,
a = -5
Substituting the value of a in (ii), we get,
b = 1 – (-5) = 6

Question 7.
Factorise x³ + 6x² + 11x + 6 completely using factor theorem.
Solution:

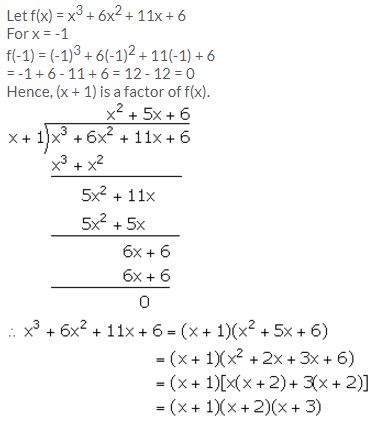
Question 8.
Find the value of ‘m’, if mx³ + 2x² – 3 and x² – mx + 4 leave the same remainder when each is divided by x – 2.
Solution:
Let f(x) = mx³ + 2x² – 3
g(x) = x² – mx + 4
It is given that f(x) and g(x) leave the same remainder when divided by (x – 2). Therefore, we have:
f (2) = g (2)
m(2)³ + 2(2)² – 3 = (2)² – m(2) + 4
8m + 8 – 3 = 4 – 2m + 4
10m = 3
m = 3/10

Question 9.
The polynomial px³ + 4x² – 3x + q is completely divisible by x² – 1; find the values of p and q. Also, for these values of p and q factorize the given polynomial completely.
Solution:
Let f(x) = px³ + 4x² – 3x + q
It is given that f(x) is completely divisible by (x² – 1) = (x + 1)(x – 1).
Therefore, f(1) = 0 and f(-1) = 0
f(1) = p(1)³ + 4(1)² – 3(1) + q = 0
p + q + 1 = 0 …(i)
f(-1) = p(-1)³ + 4(-1)² – 3(-1) + q = 0
-p + q + 7 = 0 …(ii)
Adding (i) and (ii), we get,
2q + 8 = 0
q = -4
Substituting the value of q in (i), we get,
p = -q – 1 = 4 – 1 = 3
f(x) = 3x³ + 4x² – 3x – 4
Given that f(x) is completely divisible by (x² – 1).

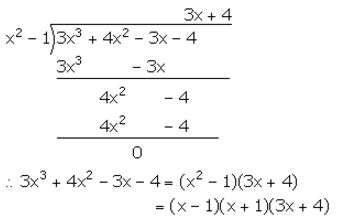
Question 10.
Find the number which should be added to x² + x + 3 so that the resulting polynomial is completely divisible by (x + 3).
Solution:
Let the required number be k.
Let f(x) = x² + x + 3 + k
It is given that f(x) is divisible by (x + 3).
Remainder = 0
f (-3) = 0
(-3)² + (-3) + 3 + k = 0
9 – 3 + 3 + k = 0
9 + k = 0
k = -9
Thus, the required number is -9.

Question 11.
When the polynomial x³ + 2x² – 5ax – 7 is divided by (x – 1), the remainder is A and when the polynomial x³ + ax² – 12x + 16 is divided by (x + 2), the remainder is B. Find the value of ‘a’ if 2A + B = 0.
Solution:
It is given that when the polynomial x³ + 2x² – 5ax – 7 is divided by (x – 1), the remainder is A.
(1)³ + 2(1)² – 5a(1) – 7 = A
1 + 2 – 5a – 7 = A
– 5a – 4 = A …(i)
It is also given that when the polynomial x³ + ax² – 12x + 16 is divided by (x + 2), the remainder is B.
x³ + ax² – 12x + 16 = B
(-2)³ + a(-2)² – 12(-2) + 16 = B
-8 + 4a + 24 + 16 = B
4a + 32 = B …(ii)
It is also given that 2A + B = 0
Using (i) and (ii), we get,
2(-5a – 4) + 4a + 32 = 0
-10a – 8 + 4a + 32 = 0
-6a + 24 = 0
6a = 24
a = 4

Question 12.
(3x + 5) is a factor of the polynomial (a – 1)x³ + (a + 1)x² – (2a + 1)x – 15. Find the value of ‘a’, factorise the given polynomial completely.
Solution:

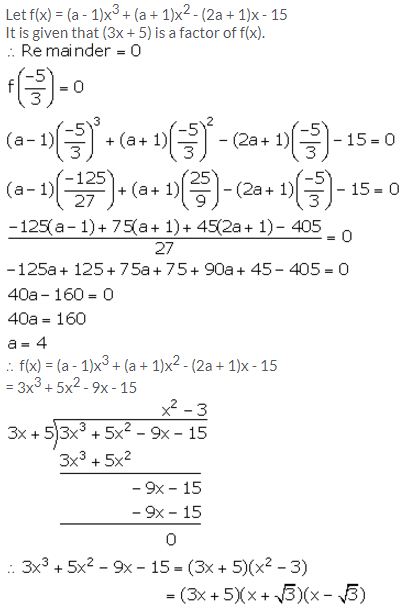
Question 13.
When divided by x – 3 the polynomials x³ – px² + x + 6 and 2x³ – x² – (p + 3) x – 6 leave the same remainder. Find the value of ‘p’.
Solution:
If (x – 3) divides f(x) = x³ – px² + x + 6, then,
Remainder = f(3) = 3³ – p(3)² + 3 + 6 = 36 – 9p
If (x – 3) divides g(x) = 2x³ – x² – (p + 3) x – 6, then
Remainder = g(3) = 2(3)³ – (3)² – (p + 3) (3) – 6 = 30 – 3p
Now, f(3) = g(3)
⇒ 36 – 9p = 30 – 3p
⇒ -6p = -6
⇒  p = 1

Question 14.
Use the Remainder Theorem to factorise the following expression:
2x³ + x² – 13x + 6
Solution:

Question 15.
Using remainder theorem, find the value of k if on dividing 2x³ + 3x² – kx + 5 by x – 2, leaves a remainder 7.
Solution:
Let f(x) = 2x³ + 3x² – kx + 5
Using Remainder Theorem, we have
f(2) = 7
∴ 2(2)³ + 3(2)² – k(2) + 5 = 7
∴ 16 + 12 – 2k + 5 = 7
∴ 33 – 2k = 7
∴ 2k = 26
∴ k = 13

Question 16.
What must be subtracted from 16x³ – 8x² + 4x + 7 so that the resulting expression has 2x + 1 as a factor?
Solution:
Here, f(x) = 16x³ – 8x² + 4x + 7
Let the number subtracted be k from the given polynomial f(x).
Given that 2x + 1 is a factor of f(x).

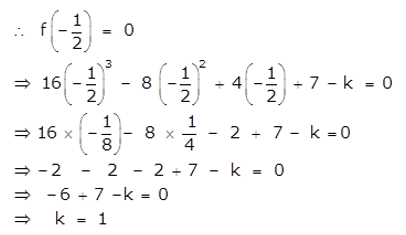
Therefore 1 must be subtracted from 16x³ – 8x² + 4x + 7 so that the resulting expression has 2x + 1 as a factor.

More Resources for Selina Concise Class 10 ICSE Solutions

• Selina ICSE Class 10 Maths Solutions
• Concise Physics Class 10 ICSE Answers
• Concise Chemistry Class 10 ICSE Answers
• Concise Biology Class 10 ICSE Answers

ICSE Solutions Selina ICSE Solutions