Selina Concise Mathematics Class 10 ICSE Solutions Geometric Progression

Selina Publishers Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression

Geometric Progression Exercise 11A – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
Find, which of the following sequence form a G.P. :
(i) 8, 24, 72, 216, ……
(ii) $\frac{1}{8}, \frac{1}{24}, \frac{1}{72}, \frac{1}{216}$ , ……..
(iii) 9, 12, 16, 24, ……
Solution 1(i).

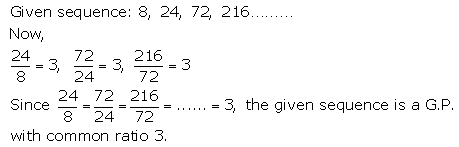
Solution 1(ii).

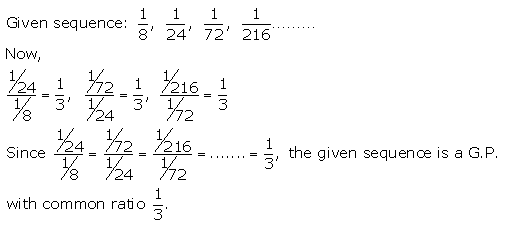
Solution 1(iii).

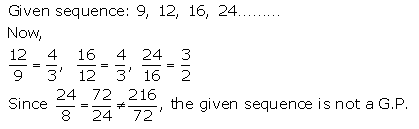
Question 2.
Find the 9th term of the series :
1, 4, 16, 64 ……..
Solution:

Question 3.
Find the seventh term of the G.P. :
1, $\sqrt{3}$ , 3, $3 \sqrt{3}$ …..
Solution:

Question 4.
Find the 8^th term of the sequence :
$\frac{3}{4}, 1 \frac{1}{2}$ 3, …….
Solution:

Question 5.
Find the 10^th term of the G.P. :
Solution:

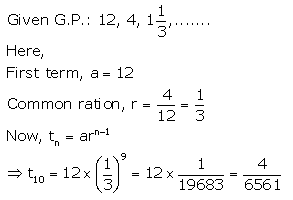
Question 6.
Find the n^th term of the series :
Solution:

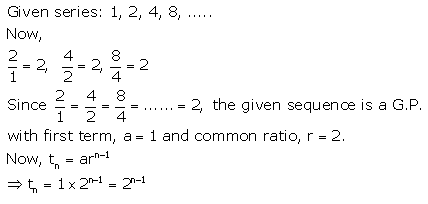
Question 7.
Find the next three terms of the sequence :
$\sqrt{5}$ , 5, $5 \sqrt{5}$ , ……
Solution:

Question 8.
Find the sixth term of the series :
2², 2³, 2⁴, ……….
Solution:

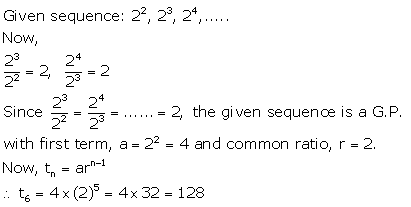
Question 9.
Find the seventh term of the G.P. :
[late]\sqrt{3}+1,1, \frac{\sqrt{3}-1}{2}[/latex], ……………..
Solution:

Question 10.
Find the G.P. whose first term is 64 and next term is 32.
Solution:

Question 11.
Find the next three terms of the series:
$\frac{2}{27}, \frac{2}{9}, \frac{2}{3}$ , ………….
Solution:

Question 12.
Find the next two terms of the series
2 – 6 + 18 – 54 …………
Solution:

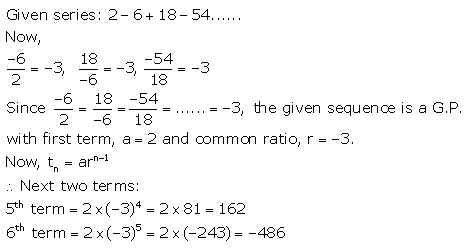
Geometric Progression Exercise 11B – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
Which term of the G.P. :

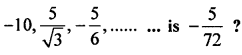
Solution:

Question 2.
The fifth term of a G.P. is 81 and its second term is 24. Find the geometric progression.
Solution:

Question 3.
Fourth and seventh terms of a G.P. are $\frac{1}{18} \text { and }-\frac{1}{486}$ respectively. Find the GP.
Solution:

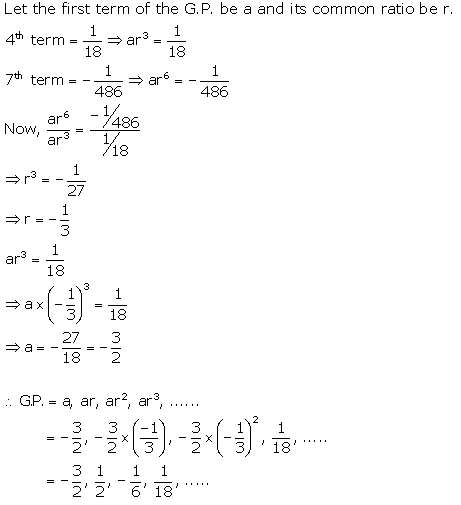
Question 4.
If the first and the third terms of a G.P. are 2 and 8 respectively, find its second term.
Solution:

Question 5.
The product of 3rd and 8th terms of a G.P. is 243. If its 4^th term is 3, find its 7^th term.
Solution:

Question 6.
Find the geometric progression with 4^th term = 54 and 7^th term = 1458.
Solution:

Question 7.
Second term of a geometric progression is 6 and its fifth term is 9 times of its third term. Find the geometric progression. Consider that each term of the G.P. is positive.
Solution:

Question 8.
The fourth term, the seventh term and the last term of a geometric progression are 10, 80 and 2560 respectively. Find its first term, common ratio and number of terms.
Solution:

Question 9.
If the 4th and 9th terms of a G.P. are 54 and 13122 respectively, find the GP. Also, find its general term.
Solution:

Question 10.
The fifth, eight and eleventh terms of a geometric progression are p, q and r respectively. Show that : q² = pr.
Solution:

Geometric Progression Exercise 11C – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
Find the seventh term from the end of the series : $\sqrt{2}$ , 2, $2 \sqrt{2}$ , ………. 32.
Solution:

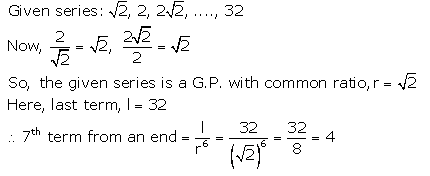
Question 2.
Find the third term from the end of the GP.
$\frac{2}{27}, \frac{2}{9}, \frac{2}{3}$ , ………….. 162
Solution:

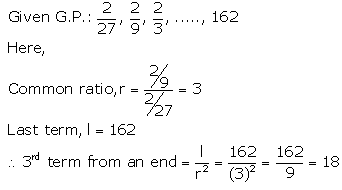
Question 3.
For the $\frac{1}{27}, \frac{1}{9}, \frac{1}{3}$ , ………… 81;
find the product of fourth term from the beginning and the fourth term from the end.
Solution:

Question 4.
If for a G.P., p^th, q^th and r^th terms are a, b and c respectively ; prove that :
(q – r) log a + (r – p) log b + (p – q) log c = 0
Solution:

Question 5.
If a, b and c in G.P., prove that : log aⁿ, log bⁿ and log cⁿ are in A.P.
Solution:

Question 6.
If each term of a G.P. is raised to the power x, show that the resulting sequence is also a G.P.
Solution:

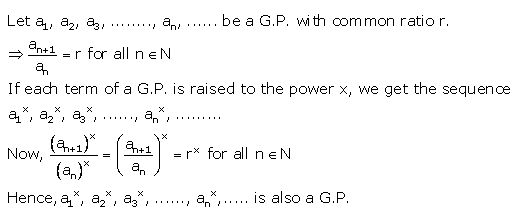
Question 7.
If a, b and c are in A.P. a, x, b are in G.P. whereas b, y and c are also in G.P. Show that : x², b², y² are in A.P.
Solution:

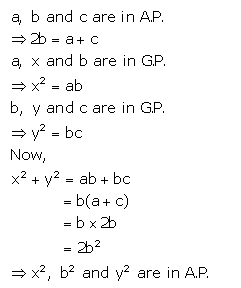
Question 8.
If a, b, c are in G.P. and a, x, b, y, c are in A.P., prove that :

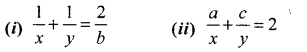
Solution 8(i).

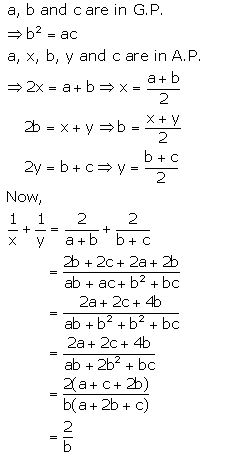
Solution 8(ii).

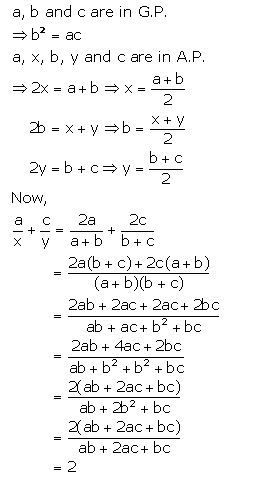
Question 9.
If a, b and c are in A.P. and also in G.P., show that: a = b = c.
Solution:

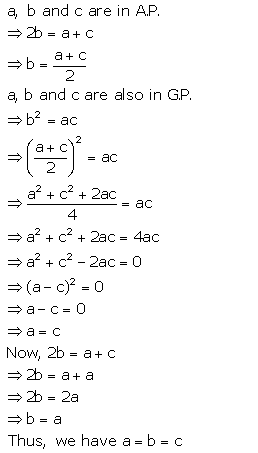
Question 10.
The first term of a G.P. is a and its n^th term is b, where n is an even number.If the product of first n numbers of this G.P. is P ; prove that : p² – (ab)ⁿ.
Solution:

Question 11.
If a, b, c and d are consecutive terms of a G.P. ; prove that :
(a² + b²), (b² + c²) and (c² + d²) are in GP.
Solution:

Question 12.
If a, b, c and d are consecutive terms of a G.P. To prove:

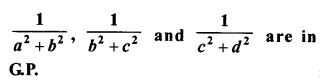
Solution:

Geometric Progression Exercise 11D – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
Find the sum of G.P. :
(i) 1 + 3 + 9 + 27 + ……….. to 12 terms.
(ii) 0.3 + 0.03 + 0.003 + 0.0003 + …… to 8 terms.

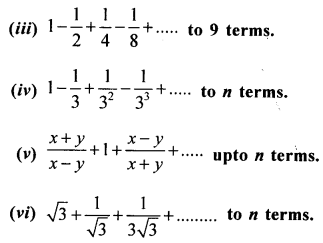
Solution 1(i).

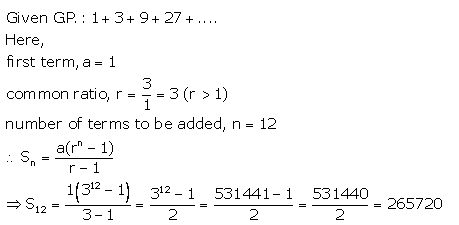
Solution 1(ii).

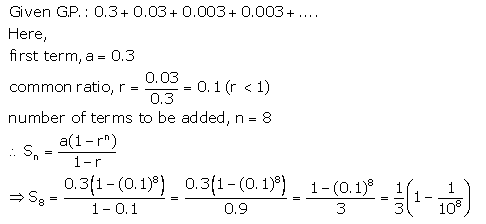
Solution 1(iii).

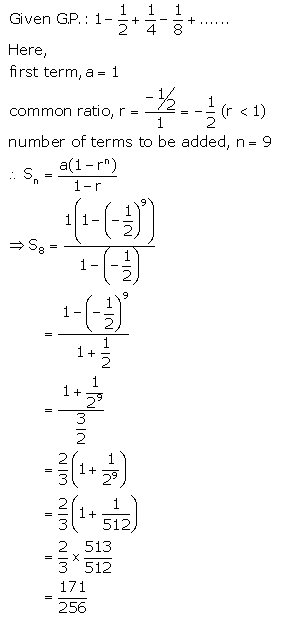
Solution 1(iv).

Solution 1(v).

Solution 1(vi).

Question 2.
How many terms of the geometric progression 1+4 + 16 + 64 + ……… must be added to get sum equal to 5461?
Solution:

Question 3.
The first term of a G.P. is 27 and its 8^th term is $\frac{1}{81}$ . Find the sum of its first 10 terms.
Solution:

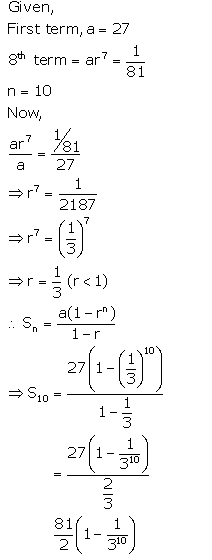
Question 4.
A boy spends ₹ 10 on first day, ₹ 20 on second day, ₹ 40 on third day and so on. Find how much, in all, will he spend in 12 days?
Solution:

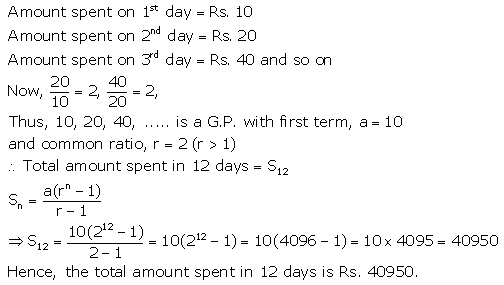
Question 5.
The 4th and the 7th terms of a G.P. are $\frac{1}{27} \text { and } \frac{1}{729}$ respectively. Find the sum of n terms of this G.P.
Solution:

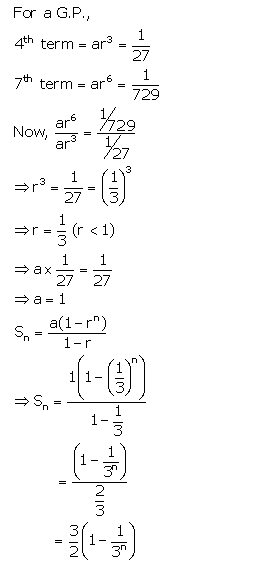
Question 6.
A geometric progression has common ratio = 3 and last term = 486. If the sum of its terms is 728 ; find its first term.
Solution:

Question 7.
Find the sum of G.P. : 3, 6, 12, ……………. 1536.
Solution:

Question 8.
How many terms of the series 2 + 6 + 18 + ………….. must be taken to make the sum equal to 728 ?
Solution:

Question 9.
In a G.P., the ratio between the sum of first three terms and that of the first six terms is 125 : 152.
Find its common ratio.
Solution:

Question 10.
Find how many terms of G.P. $\frac{2}{9}-\frac{1}{3}+\frac{1}{2}$ ………. must be added to get the sum equal to $\frac{55}{72}$ ?
Solution:

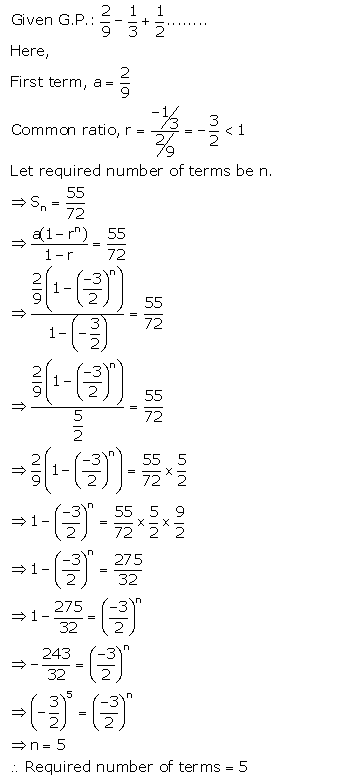
Question 11.
If the sum 1 + 2 + 2² + ………. + 2^n-1 is 255, find the value of n.
Solution:

Question 12.
Find the geometric mean between :
(i) $\frac{4}{9} \text { and } \frac{9}{4}$
(ii) 14 and $\frac{7}{32}$
(iii) 2a and 8a³
Solution 12(i).

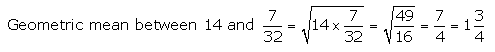
Solution 12(ii).

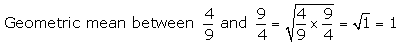
Solution 12(iii).

Question 13.
The sum of three numbers in G.P. is $\frac{39}{10}$ and their product is 1. Find the numbers.
Solution:

Question 14.
The first term of a G.P. is -3 and the square of the second term is equal to its 4^th term. Find its 7^th term.
Solution:

Question 15.
Find the 5^th term of the G.P. $\frac{5}{2}$ , 1, …..
Solution:

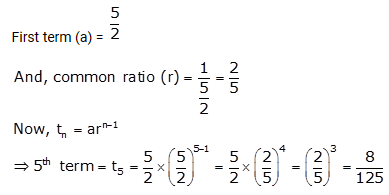
Question 16.
The first two terms of a G.P. are 125 and 25 respectively. Find the 5th and the 6th terms of the G.P.
Solution:

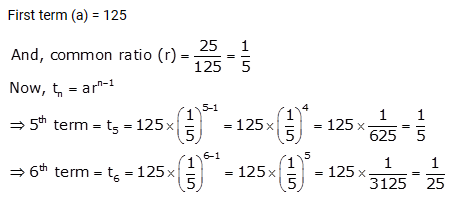
Question 17.
Find the sum of the sequence – $\frac{1}{3}$ , 1, – 3, 9, …………. upto 8 terms.
Solution:

Question 18.
The first term of a G.P. in 27. If the 8thterm be $\frac{1}{81}$ , what will be the sum of 10 terms ?
Solution:

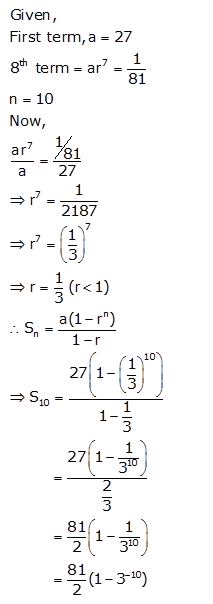
Question 19.
Find a G.P. for which the sum of first two terms is -4 and the fifth term is 4 times the third term.
Solution:

Additional Questions

Question 1.
Find the sum of n terms of the series :
(i) 4 + 44 + 444 + ………
(ii) 0.8 + 0.88 + 0.888 + …………..
Solution 1(i).

Solution 1(ii).

Question 2.
Find the sum of infinite terms of each of the following geometric progression:

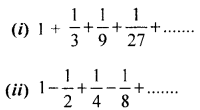
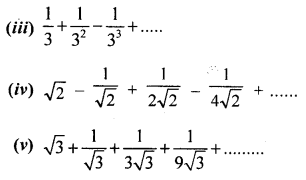
Solution 2(i).

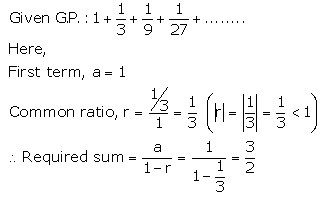
Solution 2(ii).

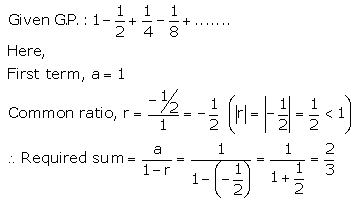
Solution 2(iii).

Solution 2(iv).

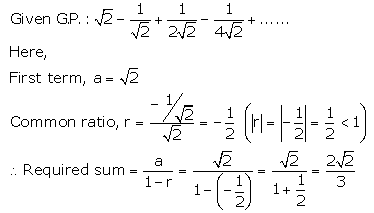
Solution 2(v).

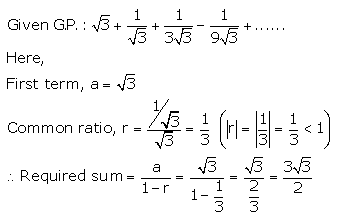
Question 3.
The second term of a G.P. is 9 and sum of its infinite terms is 48. Find its first three terms.
Solution:

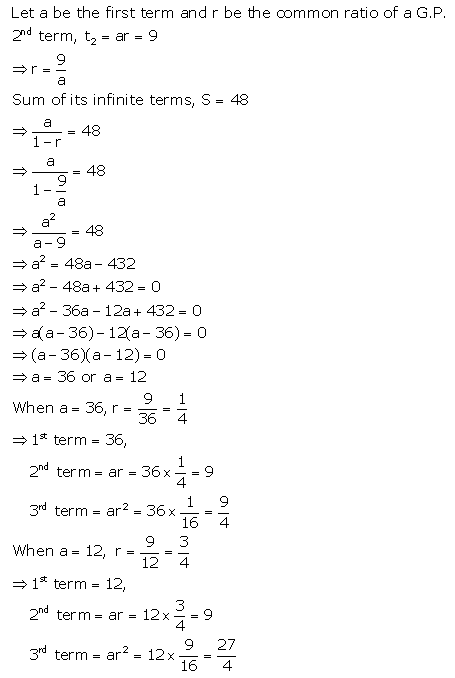
Question 4.
Find three geometric means between $\frac{1}{3}$ and 432.
Solution:

Question 5.
Find :
(i) two geometric means between 2 and 16
(ii) four geometric means between 3 and 96.
(iii) five geometric means between $3 \frac{5}{9}$ and $40 \frac{1}{2}$
Solution 5(i).

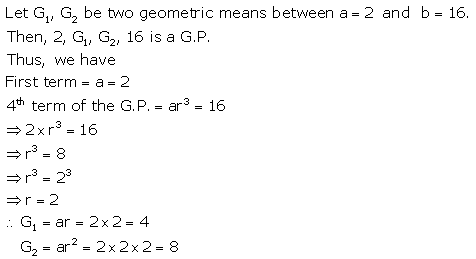
Solution 5(ii).

Solution 5(iii).

Question 6.
The sum of three numbers in G.P. is $\frac{39}{10}$ and their product is 1. Find the numbers.
Solution:
Sum of three numbers in G.P. = $\frac{39}{10}$ and their product = 1
Let number be $\frac{a}{r}$ , a, ar, then

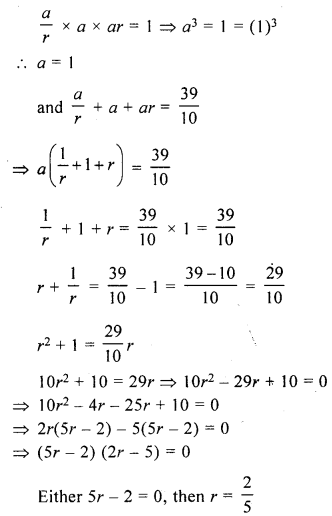
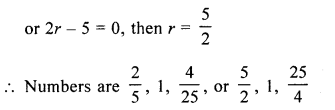
Question 7.
Find the numbers in G.P. whose sum is 52 and the sum of whose product in pairs is 624.
Solution:

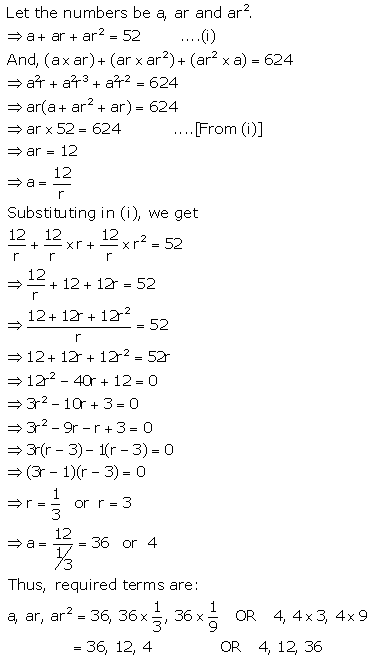
Question 8.
The sum of three numbers in G.P. is 21 and the sum of their squares is 189. Find the numbers.
Solution:

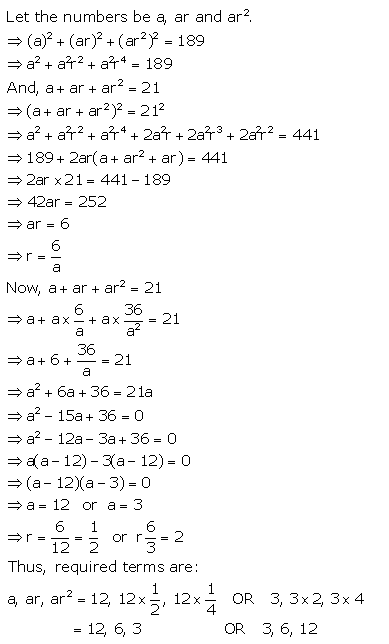
More Resources for Selina Concise Class 10 ICSE Solutions

ICSE Solutions Selina ICSE Solutions

Comments

Devesh says
February 2, 2018 at 6:11 am
Your geometric progression solutions are good but M.L Aggarwal book is much better than selina publishers mathematics for class 10 solutions. It has better explanation, more examples and BOARDS questions are also helpful.
- Dolly says
  October 11, 2018 at 3:04 pm
  Yes ml aggarwal is better than this
Suhani says
February 13, 2018 at 4:20 pm
geometric sequence problems for class 10 concise mathematics class 10 icse solutions Really helpful for last minute prparing students
R says
February 20, 2018 at 9:24 am
Thank u so much. geometric progression problems with solutions pdf helped me a lot during my board exams
Ilisha srivastava says
February 23, 2018 at 10:26 am
geometric progression problems for class 10 icse Very helpful…
Santhra says
February 26, 2018 at 5:51 pm
geometric progression for class 10 icse solutions has helped me to check my answers
Thank you so much
Shraddha says
June 15, 2018 at 7:09 am
I like geometric progression class 10 icse solutions ????????
Khushi Mehrotra says
July 21, 2018 at 6:41 am
Helpful but not arranged exercise wise. Pl. Improve it.
- Jethalalgada says
  August 28, 2018 at 12:14 pm
  Well said.
Dr. Mahipal Rohila says
July 24, 2018 at 11:04 am
These are really helpful for those students who do not get proper guidance from their teacher or tutor.
Dr. Mahipal Rohila says
July 24, 2018 at 11:06 am
Fantastic solution to gp
Ziaul haq says
July 26, 2018 at 4:20 am
It’s really helpful but not in arranged manner.
Dolly says
October 11, 2018 at 3:07 pm
It is helpful but ml aggarwal book is better
Sarthak Srivastava says
October 30, 2018 at 5:15 pm
Very impressive ????????????