Selina Concise Mathematics Class 10 ICSE Solutions Revision Paper 1
Section A (40 Marks)
(Answer all questions from this Section)
Question 1.
Find the matrix x, if y = [2101] and 2y2 = 2y + x.
Solution:
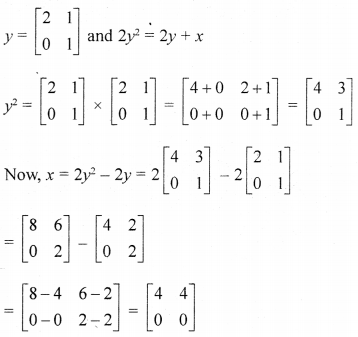
(b) A man wants to buy 124 shares availabel at ₹ 66 (par value = ₹ 50).
(i) How much should he invest ?
(ii) If the dividend is 7.5%, what will be his annual income ?
(iii) If he wants to increase income by ₹ 600, how many extra shares should he buy ?
Solution:
(i) Number of shares = 124
Market price = ₹ 66
Par value = ₹ 50
Investment = 124 × 66 = ₹ 8184
(ii) Rate of dividend = 7.5%
Face value of 124 shares = 124 × 50 = 6200
∴ Annual income = ₹ 6200×7.5100 = ₹ 465
(iii) Increased income = ₹ 600
If income is ₹ 465, then number of shares = 124
If income is ₹ 600 then number of shares = 124×600465 = 160 shares
(c) (x2 – x – 2) is factor of x3 + 3x2 + ax + b, calculate the values of a and b. Write all the factors of the given expression.
Solution:
(x2 – x – 2) is a factor of x3 + 3x2 + ax + b
If (x2 – x – 2) is a factor of x3 + 3x2 + ax + b
Then remainder will be zero
Now dividing by x2 – x – 2
Since, it is given that (x2 – x – 2) is a factor of x3 + 3x2 + ax + b
∴ Remainder is zero

⇒ (4 + a + 2)x = 0
⇒ (a + 6) = 0 ⇒ a = —6
and b + 8 = 0
⇒ b = – 8
Hence, a = -6, b = -8
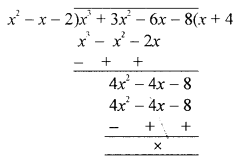
∴ f(x) = x3 + 3x2 – 6x – 8
∴ f(x) = x3 + 3x2 – 6x – 8
= (x2 – x – 2) (x + 4)
= (x – 2) (x + 1) (x + 4)
Thus, the factors of x3 + 3x2 – 6x – 8 are (x – 2) (x + 1) (x + 4)
Question 2.
(a) Find the sum of first 14 terms of the sequence -3, 3, 9, 15, …..
Solution:
Sum of first 14 terms of the sequence
-3, 3, 9, 15, …..
Here, a = -3, d = 3 – (-3) = 6
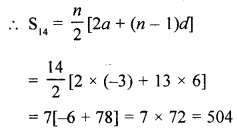
(b) The internal and external diameter of a hollow hemispherical vessel are 24 cm and 25 cm respectively. The cost to paint 1 cm2 of the surface of the vessel is ₹ 5. Find the total cost to paint the vessel all over (use π = 317).
Solution:
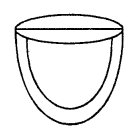
Internal diameter of hemispherical vessel = 24 cm
and outer diameter = 25 cm
∴ Inner radius (r)= 242 = 12 cm
and outer radius (R) = 252 cm
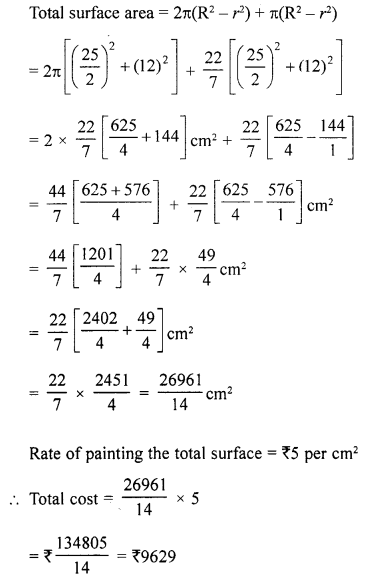
(c) Find the ratio in which the line 2x + 3y – 5 = 0 divides the line segment joining the points (8, -9) and (2, 1). Also, find the co-ordinates of the point of division.
Solution:
Let the line 2x + 3y – 5 = 0 intersects the line segment joining the points A (8, -9) and B (2, 1) in the ratio m : n at P
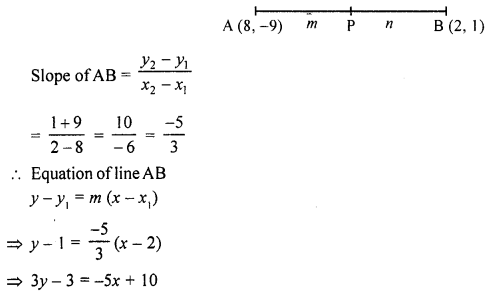
⇒ 5x + 3y = 13
⇒ 3y = 13 – 5x
Substituting the value of 3y in the given equation
2x + (13 – 5x) -5 = 0
2x + 13 – 5x -5 = 0 ⇒ -3x + 8 = 0
⇒ 3x – 8 ⇒ x = 83
Now, 3y = 13 – 403 = −13
∴y=−13×13=−19
Co-ordinates of the point P (83,−19)
Now, ratio is m : n
83=m×x2+n×x1m+n=2m+8nm+n
⇒ 8m + 8n = 6m + 24n
8m – 6m = 24n – 8n ⇒ 2m = 16n
⇒ mn=162=81
∴ Ratio is 8 : 1
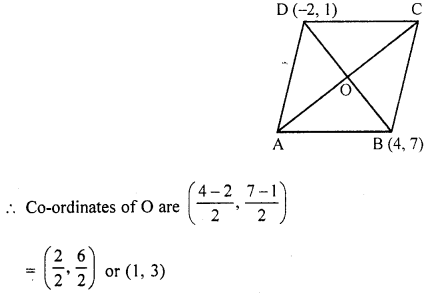
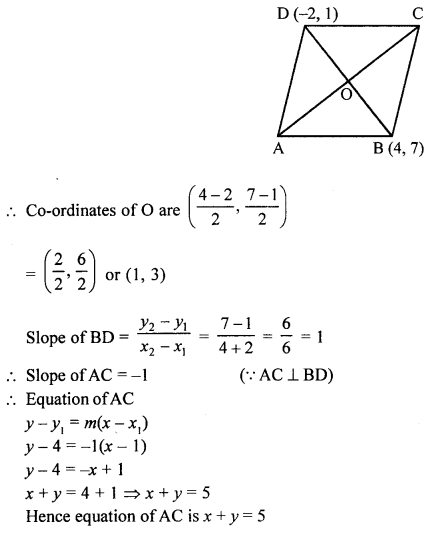
Slope of BD = y2−y1x2−x1=7−14+2=66=1
∴ Slope of AC = -1 (∵ AC ⊥ BD)
∴ Equation of AC = -1
y – y1 = m(x – x1)
y – 4 = -1(x – 1)
y – 4 = -x + 1
x + y = 4 + 1 ⇒ x + y = 5
Hence equation of AC is x + y = 5
Question 3 :
(a) The given figure shows a circle (with centre O) inscribed in a right-angled triangle ABC with ∠B = 90°, AB = 8 cm and BC = 6 cm. Find :
(i) the radius of the circle.
(ii) the area of the shaded portion i.e. portion enclosed between the circle and the triangle.
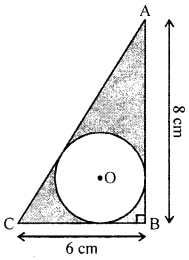
Solution:
The incircle touches the sides of right triangle
ABC at P, Q and R respectively

CB = x + y – 6 cm
AB =y + z = 8 cm
AC = z + x = 10 cm
Adding,
2(x + y + z) = 24 24
x + y + z = 242 = 12
∴ z = 12 – 6 = 6 cm
x = 12-8 = 4 cm
y = 12 – 10 = 2 cm
(i) Radius of the incircle = y = 2 cm
(ii) Now area of shaded portions
= Area of ∆ABC – area of circle
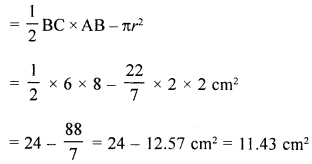
(b) Find the median of the data : 19, 25, 59, 48, 35, 31, 30, 32, and 51. If 25 is replaced by 52, what will be the new median ?
Solution:
The given data is 19, 25, 59, 48, 35, 31, 30, 32, 51
Arranging in ascending order,
19, 25, 30, 31, 32, 35, 48, 51, 59
⇒ N = 9
∵ There are odd.
∴ It’s median = 9+12 term = 5th term= 32
(ii) If 25 is replaced by 52, then
19, 30, 31, 52, 35, 48, 51, 52, 59
Median = 5th term is 35
(c) Mahima has a recurring deposit account in a bank for 3 years at 8% p.a. If she gets ₹ 3,996 as interest at the time of maturity of the scheme, find :
(i) the monthly instalment.
(ii) the maturity amount.
Solution:
Let monthly instalment = P
Period = 3 years = 36 months
Rate = 8% p.a.
Interest = ₹ 3996

∴ Monthly instalment = ₹ 900
(ii) Maturity value = ₹ 900 × 36 + ₹ 3996
= ₹ 32400 + ₹ 3996 = ₹ 36396
Question 4 :
(a) (i) If sec θ.sin(36° + θ) = 1, find the value of θ so that θ and 36° + θ are acute angles.
(ii) Find θ, if sin 5θ = cos 4θ; where 5θ and 4θ are acute angles.
Solution:
(i) sec θ sin (36° + θ) = 1
⇒ cosec (90° – θ) sin (36° + θ) = 1
⇒ 90° – θ = 36° + θ
90° – 36° = θ + θ ⇒ 2θ = 54°
θ=54∘2=27∘
(ii) sin 5θ = cos 4θ
= sin (90° – 4θ)
∴ 5θ = 90°-4θ
⇒ 5θ + 4θ = 90° ⇒ 9θ = 90°
θ = 10°
(b) Points (4, 0) and (-3, 0) are invariant points under reflection in line L1; points (0, 5) and (0, -2) are invariant under reflection in line L2.
(i) Name and write the equations of lines L1 and L2.
(ii) Write P’, the reflection of P (6, -8) in L1 and P” the image of P in L2.
(iii) State a single transformation that maps P’ onto P”.
Solution:
(i) ∵ The ordinate of points (4, 0) and (-3, 0) is zero
∴ L1 is x-axis and its equation is y = 0
and similarly the abscissa of points (0, 5) and (0, -2) is zero .
L2 is y-axis and its equation is x = 0
(ii) ∵ P’ is the reflection of P (6, -8) in L1 and P” is the reflection of P in L2
∴ Co-ordinates of P’ are (6, 8) and of P” is (-6, -8)
(iii) The single transformation that maps P’ and P” is reflection in origin.
(c) Which of the following arguments are correct and which are incorrect ? Give reason if incorrect.
(i) If two coins are tossed simultaneously there are three possible outcomes :- two heads, two tails or one of each. Therefore, for each of these outcomes, probability is 13.
(ii) If a dice is thrown, there are two possible outcomes an odd number or an even number Therefore the probability of an odd number is 12.
Solution:
(i) Incorrect.
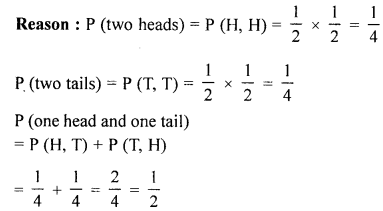
(ii) Correct
Reason : The numbers on the faces of a dice are 1, 2, 3, 4, 5 and 6.
∴ Odd numbers = 1, 3, 5
and Even number = 2, 4, 6
∴ P (odd number) = 36=12
Section B (40 Marks)
(Answer any four questions from this Section)
Question 5.
(a) A cone of radius 4 cm is divided into two parts by drawing a plane through the mid-point of its axis and parallel to its base. Compare the volumes of the two parts.
Solution:
Radius of the cone (R) = 4 cm
It is divided into two parts through the mid point of the axis (height of the cone).
Let height be h

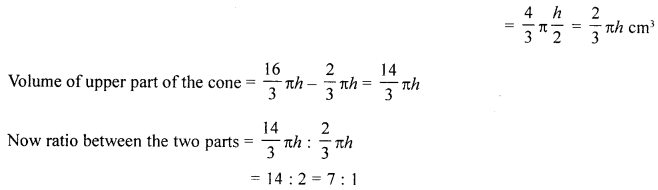
(b) If P=[6−24−6] and Q=[5320], find the matrix M such that 2Q – 3P – 3M = 0.
Solution:
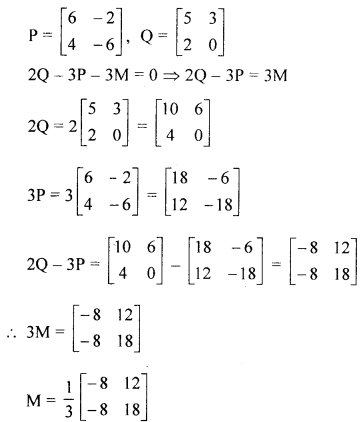
(c) For the following sequence in G.P., find the sum of infinite terms:
Solution:
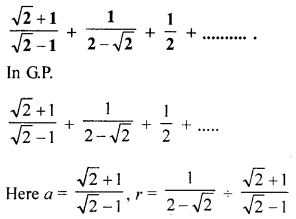
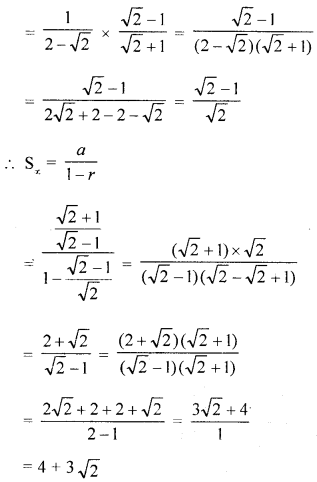
Question 6.
(a) The radius and height of a cone are in the ratio 3 : 4. If its volume is 301.44 cm3, find :
(i) its radius,
(ii) its slant height. [Take π = 3.14]
Solution:
Ratio in radius and height of a cone = 3:4
Volume = 301.44 cm3
Let radius be 3x and height = 4x
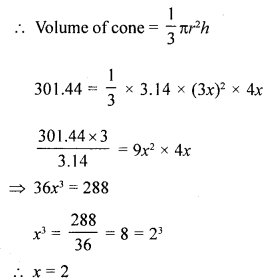
(i) ∴ Radius = 3x = 2 × 3 = 6 cm
(ii) and height = 2 × 4 = 8 cm
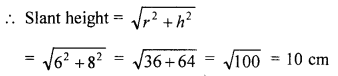
(b) Given P = {A: : 5 < 2x – 1 ≤ 11, x ϵ R} and Q = {x : – 1 ≤ 3 + 4x < 23, x ϵ I}, where R = {real numbers} and I = {integers}.
(i) Represent P and Q on number lines.
(ii) Write down the elements of P ∩ Q.
Solution:
P = {x : 5 < 2x – 1 ≤ 11, x ϵ R}
Q = {x : -1 ≤ 3 + 4x < 23, x ϵ I}
P = {x : 5 < 2x – 1 ≤ 11, x ϵ R}
∴ 5 < 2x – 1 ≤ 11
5 < 2x – 1 ⇒ 6 < 2x
⇒ 3 < x
and 2x – 1 ≤ 11 ⇒ 2x ≤ 11 + 1 = 12
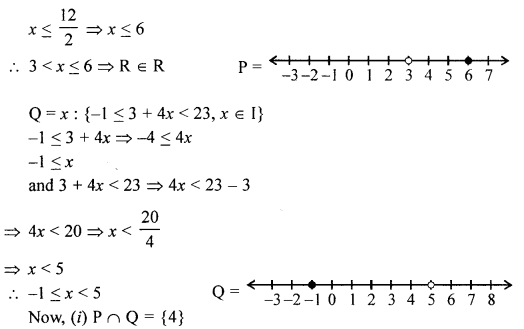
(c) A solid cylinder has diameter 28 cm and height 24 cm. A conical cavity of the same diameter and the same height is drilled out from this solid. Find the whole surface area of the remaining solid.
Solution:
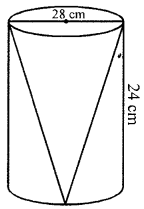
Diameter of the solid cylinder = 28 cm
Radius (r) = 282 = 14 cm
and height (h) = 24 cm
A conical cavity drilled out of the same radius and height
∴ Whole surface area = πrl + 2πrh + πr2 = πr(l + 2h + r)
= 227 × 14[27.78 + 48 + 14] cm2
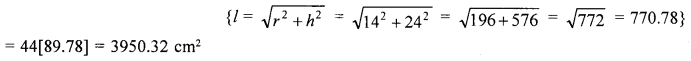
Question 7.
(a) Find the length of canvas, 2 m in width, required to make a conical tent, 12 m in diameter and 12.6 m in slant height. Also, find the cost of canvas at the rate of ₹ 112.50 per metre.
Solution:
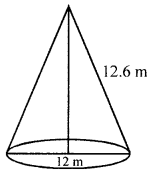
Diameter of the tent = 12 m
∴ Radius (r) =122 = 6 m
Slant height (l) = 12.6 m
∴ Curved surface area = πrl
=227×6×12.6m2=237.6m2
Width of canvas = 2 m
∴ Length = Area Width =237.62=118.8m
Rate of canvas = ₹ 112.50 per metre
Total cost = ₹ 118.8 × ₹ 112.50 = ₹ 13365
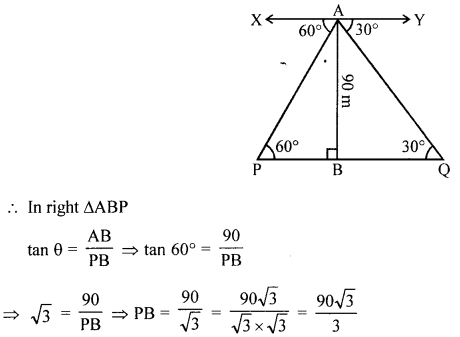
(b) P and Q are two points on the opposite sides of a 90 m high tower AB. the base B, of the tower AB, and points P and Q are along the same straight line, the angles of depression of points P and Q as observed from top A of tower AB are 60° and 30° respectively. Find, correct to the nearest metre, the distance between P and Q.
Solution:
P and Q are two points on opposite sides of a tower AB = 90 m
P and Q are on the same line
Angle of depression from A to the two given points are 60° and 30° respectively

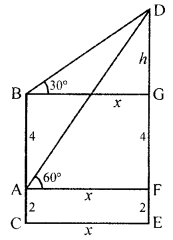
(c) The lower window of a house is at a height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At a certain instant, the angles of elevation of a balloon from these windows are observed to be 60° and 30° respectively. Find the height of the balloon above the ground.
Solution:
Let A be the lower window which is 2 m about the ground and B is upper window Which is 4 m above the lower and D is the balloon.
DE is its height
Angles of elevation from windows A and B to the balloon are
60° and 30° respectively.
Let BG = AF = CE = x m and DG = h m
In the right ∆DBG

Question 8.
(a) In the given figure, CM and RN are respectively the medians of triangles ABC and PQR.
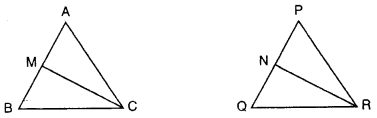
If ∆ABC is similar to ∆PQR, prove that:
(i) ∆AMC ~ ∆PNR,
(ii) CMRN=ABPQ and
(iii) ∆CMB ~ ∆RNQ
Solution:
In the given figure, CM and RN are medians of ∆ABC and ∆PQR respectively ∆ABC ~ ∆PQR
To prove : (i) ∆AMC ~ ∆PMR


∆CMR ~ ∆RNQ (by SAS axiom)
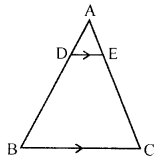
(b) In the given figure, DE // BC and AD : DB = 2 : 5. Find :
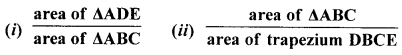
Solution:
(i) In the given figure, DE || BC
and AD : DB = 2 : 5

(c) A m an holds 800 shares of ₹ 100 each of a company paying 7.5% dividend semi-annually,
(i) Calculate his annual dividend.
(ii) If he had bought these shares at 40% premium, what percentage return does he get on his investment ?
Solution:
Number of shares = 800
Face value = ₹ 100
Dividend = 7.5% semi annually or 15% annually
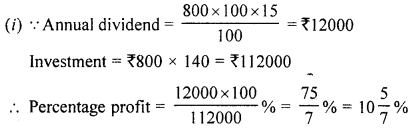
Question 9 :
(a) Two customers A and Bare visiting a particular shop in the same week (Tuesday to Saturday). Each is equally likely to visit the shop on any day as on another day. What is the probability that both will visit the shop on :
(i) the same day ?
(ii) consecutive days ?
(iii) different days ?
Solution:
Two persons are A and B and number of days = 5 (Tuesday to Saturday)
Total number of outcomes = 5 × 5 = 25
(i) The same day
Total number of favourable outcomes = J
(TT, WW, Th, Th, FF SS)
∴ Probability P(E) = 525=15
(ii) Fn consecutive days TW, WTh, ThF, WT,FS, SF, ThW, FTh = 8 8
∴ Probability = 825
(iii) On different days (Absent on the same days)
Number of favourable outcomes =1 – (P) of favourable outcomes on same day
=1−15=45
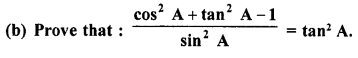
Solution:
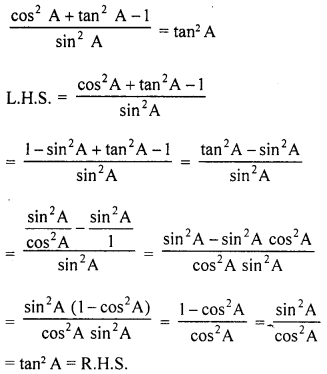
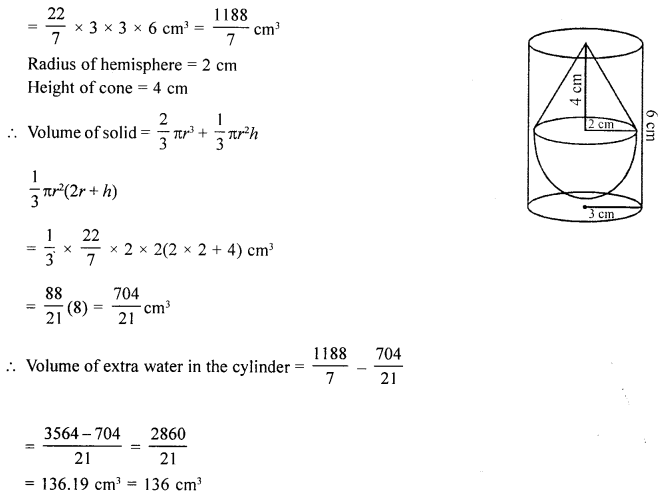
(c) A solid consisting of a right circular cone, standing on a hemisphere, is placed upright, in a right circular cylinder, full of water, and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and’its height is 6 cm; the radius of the hemisphere is 2 cm and the height of the cone is 4 cm. Give your answer correct to the nearest centimetre (Take π = 317).
Solution:
Radius of cylinder = 3 cm
and height = 6 cm
∴ Volume = πr2h
Question 10.
(a) Construct an angle ABC = 45°. Mark a point P on BC such that BP = 4.8 cm. Construct a circle to touch AB at B and also to pass through P.
Solution:
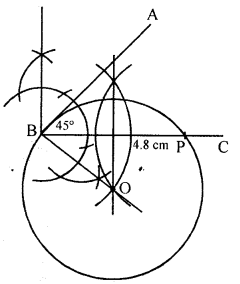
Steps of construction :
(i) Draw an angle ABC = 45°.
(ii) Take a point P on BC such that BP = 4.8 cm.
(iii) Draw the perpendicular bisector of BP.
(iv) Draw perpendicular on AB at B which intersects the perpendicular bisector of BP at O.
(v) With centre O and radius OB, draw a circle which passes through P and touches AB at B.
(b) In the given figure, ABCD is a parallelogram and AP : PB = 3 : 5. Calculate :
(i) area (∆PBN) : area (trapezium APND)
(ii) PN : BC and area (∆PMN) : area (∆BMC)
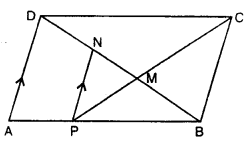
Solution:
In the given figure, ABCD is a ||gm
P isa point on AB
Such that AP : PB = 3 : 5
Calculate:
(i) area (∆PBN): area (trapezium APND)
(ii) PN : BC and area (∆PMN) : area (∆BMC)

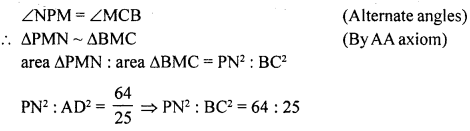
(c) In the given figure, PQL and PRM are two tangents to the circle with centre O at the point Q and R respectively. If S is a point on the circle such that angle SQL = 50° and angle SRM = 60°. Find the reflex angle QOR.
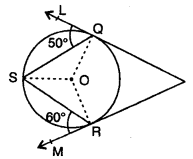
Solution:
In the given figure, PQL and PRM are two tangents to the circle in the centre O at Q and R. S is a point on the circle such that ∠SQL = 50° and ∠SRM = 60°
To find : reflex ∠QOR
∴ OQ is radius and PQ is tangent
∴ ∠OQL = 90°
and ∠OQS = 90° – 50° = 40°
and ∠QSO = 40° (∵ OQ = OS radii if the same circle)
∴ ∠ORS = 90° – 60° = 30°
∴ ∠OSR = ∠ORS = 30°
∴ ∠QSR = 40° + 30° = 70°
∵ arc QOR subtends ∠QOR at the centre and ∠QSR at the remaining part of the circle
∴ ∠QOR = ∠QSR = 2 x 70° = 140°
and reflex ∠QOR = 360° – 140° = 220°
Question 11.
(a) If the mid-point of the line segment joining the points A (3, 4), B (A, 6) is P (x, y) and x + y – 10 = 0, find the value of A.
Solution:
Mid-point of the line segment joining the points A (3, 4) and B (k, 6) is P (x, y)
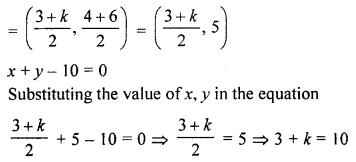
k = 10 – 3 = 7
(b) A conical tent is to accomodate 11 persons. Each person must have 4 sq. m of the space on the ground and 20 cubic metre of air to breath. Find the height of the tent.
Solution:
Space of one person = 4 sq. m
∴ Space for 11 persons = 4 × 11 = 44 m2
∴ Area of ground of conical tent = 44 m2
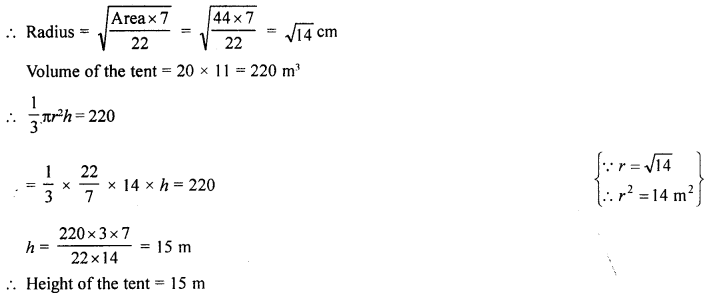
Height of the tent = 15 m
(c) (i) If two angles A and B are acute such that 2 sin (A + B) = √3 and 2 cos (A – B) = √3 find the values of angles A and B.
(ii) ABCD is a rhombus. The co-ordinates of vertices B and D are (4, 7) and (-2, 1) respectively.
Find the equation of AC.
Solution:
A and B are acute angles.

(ii) In rhombus,
Co-ordinates of B are (4, 7) and of D are (-2, 1)
∵ The diagonals of a rhombus bisect each other at right angles