Rules for Dealing with Chords, Secants, Tangents in Circles
Theorem 1:
If two chords intersect in a circle, the product of the lengths of the segments of one chord equal the product of the segments of the other.
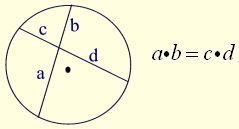 Intersecting Chords Rule:
Intersecting Chords Rule:
(segment piece)×(segment piece) = (segment piece)×(segment piece)
Theorem Proof:

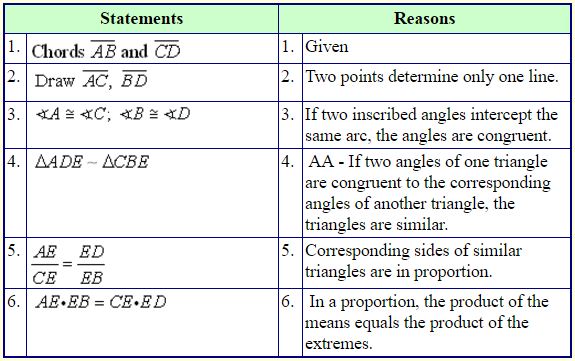 Theorem 2:
Theorem 2:
If two secant segments are drawn to a circle from the same external point, the product of the length of one secant segment and its external part is equal to the product of the length of the other secant segment and its external part.
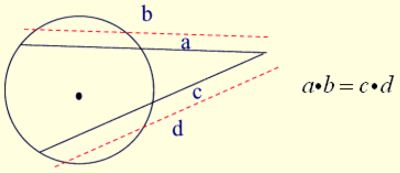 Secant-Secant Rule:
Secant-Secant Rule:
(whole secant)×(external part) = (whole secant)×(external part)
Theorem 3:
If a secant segment and tangent segment are drawn to a circle from the same external point, the product of the length of the secant segment and its external part equals the square of the length of the tangent segment.
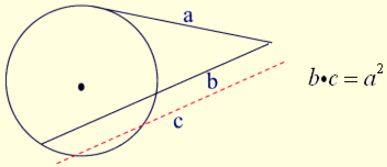 Secant-Tangent Rule:
Secant-Tangent Rule:
(whole secant)×(external part) = (tangent)2
This theorem can also be stated as “the tangent being the mean proportional between the whole secant and its external part” (which yields the same final rule:

