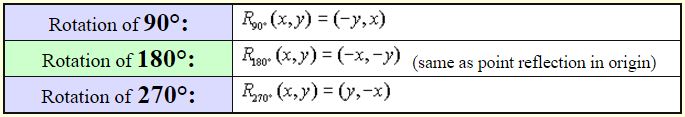Rotations
A rotation is a transformation that turns a figure about a fixed point called the center of rotation. Rays drawn from the center of rotation to a point and its image form an angle called the angle of rotation. (notation Rdegrees )
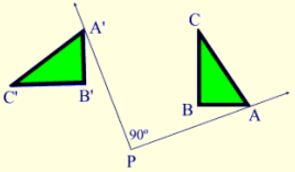An object and its rotation are the same shape and size, but the figures may be turned in different directions.
Properties preserved (invariant) under a rotation:
- distance is preserved (lengths of segments are the same)
- angle measures (remain the same)
- parallelism (parallel lines remain parallel)
- colinearity (points stay on the same lines)
- midpoint (midpoints remain the same in each figure)
- orientation (lettering order remains the same)
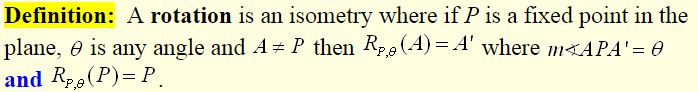
So what is this definition saying:
Part I (up to the word “and”): Here we see an example where the angle is 90 degrees. The center of rotation is point P and point A is distinct from point P. In addition to point A, we also have points B and C forming triangle ABC.
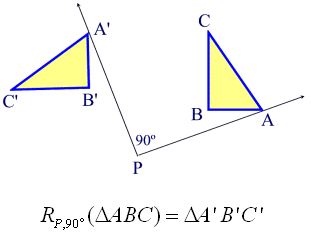Part II (after the word “and”): The second part of the definition deals with point P being rotated about itself. Rotating a POINT about itself creates no noticeable changes. The image from this rotation will be the same point P that you started with. This is represented by RP,θ(P) = P
A rotation turns a figure through an angle about a fixed point called the center.
When working in the coordinate plane, assume the center of rotation to be the origin unless told otherwise. A positive angle of rotation turns the figure counterclockwise, and a negative angle of rotation turns the figure in a clockwise direction.
