Transformations – Notations and Formulas
A transformation is an operation that maps an initial figure (pre-image) onto a final image called an image.
Line Reflections
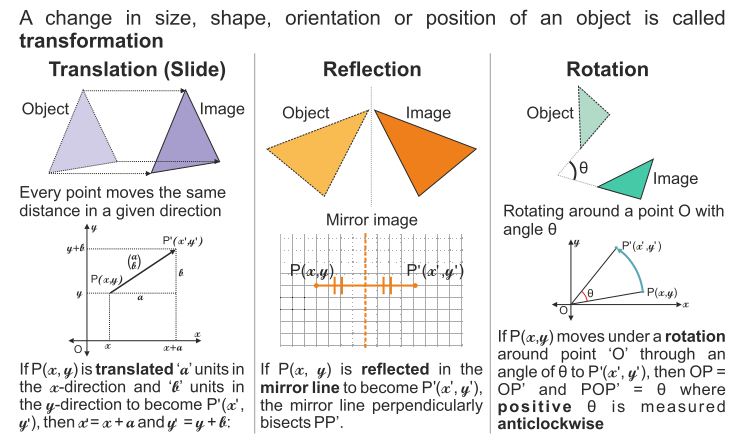
A reflection is a flip. It is an opposite isometry – the image does not change size but the lettering is reversed.

Point Reflections
A point reflection exists when a figure is built around a single point called the center of the figure. It is a direct isometry.
Reflection in the Origin: While any point in the coordinate plane may be used as a point of reflection, the most commonly used point is the origin.
P(x,y)→P’(-x,-y) or rorigin(x,y) = (-x,-y)
Rotations (assuming center of rotation to be the origin)
A rotation turns a figure through an angle about a fixed point called the center. A positive angle of rotation turns the figure counterclockwise, and a negative angle of rotation turns the figure in a clockwise direction. It is a direct isometry.

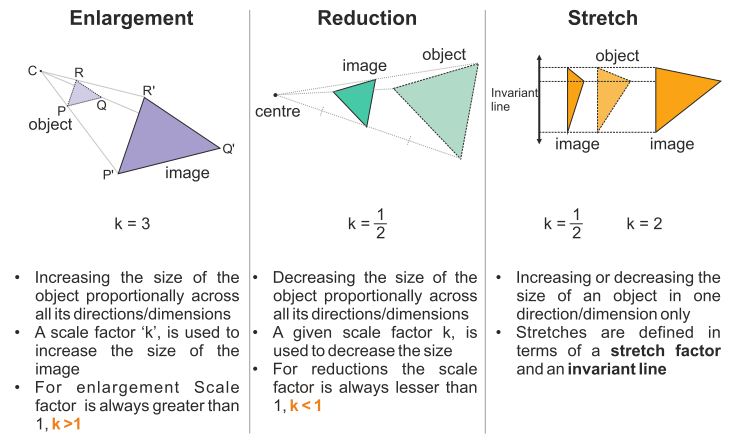
Dilations
A dilation is a transformation that produces an image that is the same shape as the original, but is a different size. NOT an isometry. Forms similar figures.
Dilation of scale factor k:
The center of the dilation is assumed to be the origin unless otherwise specified.
Dk (x, y) = (kx, ky)
Translations
A translation “slides” an object a fixed distance in a given direction. The original object and its translation have the same shape and size, and they face in the same direction. It is a direct isometry.
Translation of h, k:
Th,k(x, y) = (x+h, y+k)
