What is the Relationship between a Mole and Avogadro's number

What is the Relationship between a Mole and Avogadro’s number

Avogadro’s number
Atoms and molecules are so small in size that they cannot be counted individually. The chemists use the unit mole for counting atoms, molecules or ions. It is represented by n.
A mole represents 6.022 × 10²³ particles.
Example: 1 mole of atoms = 6.022 × 10²³ atoms.
1 mole of molecules = 6.022 × 10²³ molecules The number of particles present in 1 mole of any substance is fixed i.e. 6.022 × 10²³.
This number is called Avogadro constant or Avogadro number. it is represented by No.
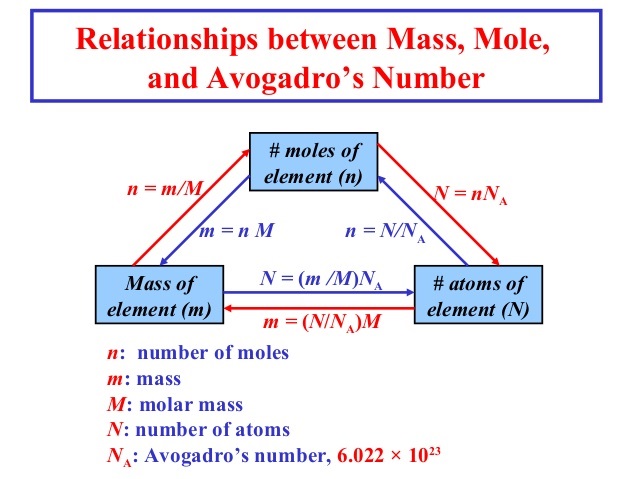
1 mole of atoms = 6.022 × 10²³ atoms = Gram atomic mass or Molar mass of element
Number of moles = \(\frac { Mass\quad of\quad element }{ Molar\quad mass } \)
n =  \(\frac { m }{ M }  \)
Number of moles =  \(\frac { Given\quad number\quad of\quad atoms }{ Avagadro\quad number } \)
n =  \(\frac { N }{ { N }_{ 0 } } \)
No. of moles = n
Given mass = m
Molar mass = M
Given number of particles = N
Avogadro number of particles = N₀
These relations can be interchanged as
Mass of element, m = n × M
or No. of particles of element, N = n × N₀
Similarly,
1 Mole of molecules = 6.022 × 10²³ molecules
= Gram molecular mass of Molar mass
Number of moles =  \(\frac { Mass\quad of\quad substance }{ Molar\quad mass } \)
n =   \(\frac { m }{ M }  \)
Number of moles
=  \(\frac { Given\quad number\quad of\quad molecules }{ Avagadro\quad number } \)
n =  \(\frac { N }{ { N }_{ 0 } } \)
or m = n × M and N = n × N₀

Relationship between mole, number of particles and mass and interconversion of one into the other.

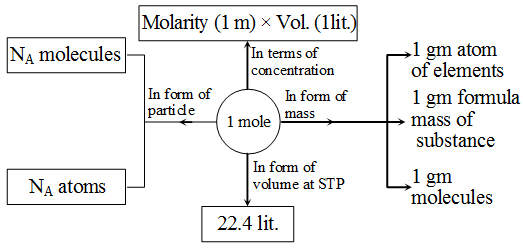
Molarity (M) : Moles of solute is one litre of solution is known as molarity .
M =  \(\frac { Number\quad of\quad moles\quad of\quad solute }{ Volume\quad of\quad solution\quad in\quad litre } \)

Example 1: An ornament of silver contains 20 g of silver. Calculate the moles of silver present (atomic mass of silver = 180 u)
Solution: Moles of silver,
n = \(\frac { m }{ M } \)
Mass of silver, m = 20 g,
Molar mass of silver,
M = 108 g
∴ n =  \(\frac { 20 }{ 108 }  \) = 0.185 mol.

Example 2: How many moles of CO₂ are present in 51.2 g of it ?
Solution: Molecular mass of CO₂ = 12 + 2 + 16 = 44 u
Molar mass of CO₂ (M) = 44 g
Mass of CO₂ (m) = 51.2 g
Moles of CO₂,
n = \(\frac { m }{ M } =\frac { 51.2 }{ 44 } \) = 1.16 mol.

Example 3: Calculate the mass of
(i)  0.5 moles of N₂ gas
(ii) 0.5 moles of N atoms
Solution: (i) 0.5 moles of N₂ gas
Mass = Molar mass × Number of moles
m = M × n
M = 28 g, n = 0.5
∴ m = 28 × 0.5 = 14 g
(ii) Mass = Molar mass × Number of moles
m = M × n
n = 0.5 mole, M = 14 g
m = 14 × 0.5 = 7 g

Mass percentage of an element from molecular formula :
The molecular formula of a compound may be defined as the formula which specifies the number of atoms of various elements in the molecule of the compound.
Example: The molecular formula of glucose is C₆H₁₂O₆. This indicates that a molecule of glucose contains six atoms of carbon, twelve atoms of hydrogen and six atoms of oxygen.
The mass percentage of each element is then calculated by the following formula : Mass percentage of element X
= \(\frac { Mass\quad of\quad X\quad in\quad one\quad mole }{ Gram\quad molecular\quad mass } \times 100\)

Example 1: Calculate the percentage composition (by mass) of formaldehyde (CH₂O).
Solution: Molecular mass of formaldehyde,
CH₂O = 12 × 1 + 1 × 2 + 16 × 1 = 30
Mass of one mole of formaldehyde = 30 g
1 Mole of CH₂O contains 1 mole (12 g) of carbon. 2 moles of hydrogen (2 g) and 1 mole of oxygen (16 g)
Percentage of carbon = \(\frac { 12g }{ 30g }\times 100\) = 40.0%
Percentage of hydrogen = \(\frac { 2g }{ 30g }\times 100\) = 6.7%
Percentage of oxygen = \(\frac { 16g }{ 30g }\times 100\) = 53.3%

Empirical formula
The empirical formula of a compound may be defined as the formula which gives the simplest whole number ratio of atoms of the various elements present in the molecule of the compound.
Example: The empirical formula of the compound glucose (C₆H₁₂O₆), is CH₂O which shows that C, H, and O are present in the simplest ratio of 1 : 2 : 1.
Rules for writing the empirical formula
The empirical formula is determined by the following steps :

1. Divide the percentage of each elements by its atomic mass. This gives the relative number of moles of various elements present in the compound.
2. Divide the quotients obtained in the above step by the smallest of them so as to get a simple ratio of moles of various elements.
3. Multiply the figures, so obtained by a suitable integer, if necessary, in order to obtain whole number ratio.
4. Finally write down the symbols of the various elements side by side and put the above numbers as the subscripts to the lower right hand corner of each symbol. This will represent the empirical formula of the compound.

Example: A substance, on analysis, gave the following composition : Na = 43.4%, C = 11.3%, O = 45.3%. Calculate its empirical formula
[Atomic masses = Na = 23, C = 12, O = 16]
Solution:    

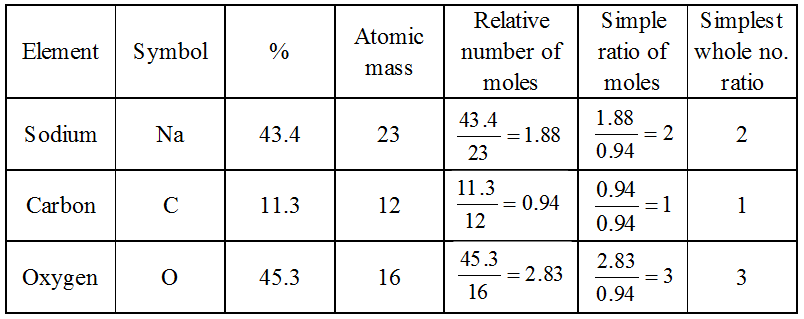
Therefore, the empirical formula is Na₂CO₃

Determination molecular formula :
Molecular formula = Empirical formula × n
n = \(\frac { Molecular\quad formula }{ Empirical\quad formula } \)
Example 1: What is the simplest formula of the compound which has the following percentage composition : Carbon 80%, Hydrogen 20%, If the molecular mass is 30, calculate its molecular formula.
Solution: Calculation of empirical formula :

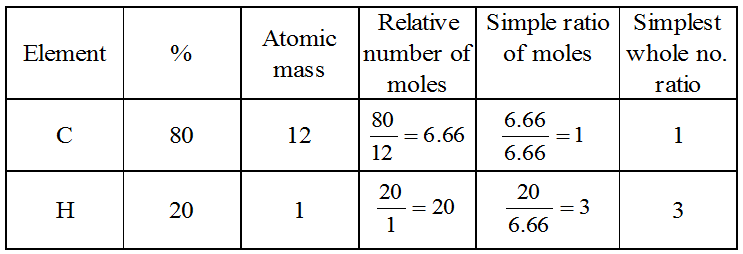
∴ Empirical formula is CH₃.
Calculation of molecular formula :
Empirical formula mass = 12 × 1 + 1 × 3 = 15
n = \(\frac { Molecular\quad mass }{ Empirical\quad formula\quad mass } =\frac { 30 }{ 15 } \) = 2
Molecular formula
= Empirical formula × 2 = CH₃ × 2 = C₂H₆.

Example 2: On heating a sample of CaCO₃, volume of CO₂ evolved at NTP is 112 cc. Calculate
(i) Weight of CO₂ produced
(ii) Weight of CaCO₃ taken
(iii) Weight of CaO remaining
Solution: (i) Mole of CO₂ produced  \(\frac { 112 }{ 22400 } =\frac { 1 }{ 200 } \) mole
mass of CO₂ = \(\frac { 1 }{ 200 } \times 44\) = 0.22 gm
(ii) CaCO₃  →  CaO   +  CO₂(1/200 mole)
mole of CaCO₃ = \(\frac { 1 }{ 200 }  \) mole
∴ mass of CaCO₃ = \(\frac { 1 }{ 200 } \times 100\) = 0.5 gm
(iii) mole of CaO produced = \(\frac { 1 }{ 200 }  \) mole
mass of CaO = \(\frac { 1 }{ 200 } \times 56\) = 0.28 gm
* Interesting by we can apply
Conversation of mass or wt. of CaO
= wt. of CaCO₃ taken – wt. of CO₂ produced
= 0.5 – 0.22 = 0.28 gm

Example 3: If all iron present in 1.6 gm Fe₂O₃ is converted in form of FeSO₄. (NH₄)₂SO₄.6H₂O after series of reaction. Calculate mass of product obtained.
Solution: If all iron will be converted then no. of mole atoms of Fe in reactant & product will be same.
∴ Mole of Fe₂O₃ = \(\frac { 1.6 }{ 160 } =\frac { 1 }{ 100 } \)
mole atoms of Fe = 2 × \(\frac { 1 }{ 100 } =\frac { 1 }{ 50 } \)
mole of FeSO₄. (NH₄)₂SO₄.6H₂O will be same as mole atoms of Fe because one atom of Fe is present in one molecule.
∴ Mole of FeSO₄.(NH₄)₂.SO₄.6H₂O = \(\frac { 1 }{ 50 } \)
∴ Mass = \(\frac { 1 }{ 50 } \) × Molecule wt.
= \(\frac { 1 }{ 50 } \times 342\) = 7.84 gm.

Example 4: Calculate mass of hydrazine N­₂H₄ obtained when 1.12 litre of N₂ taken at NTP reacts with H₂ according to N₂ + 2H₂  →  N₂H₄.
Solution: Moles of N₂ taken = \(\frac { 1.12 }{ 22.4 } =\frac { 1 }{ 20 } \)
N₂              +            2H₂   →   N₂H₄
(1/20 mole)                             (1/20 mole)
mass of N₂H₄ = \(\frac { 1 }{ 20 } \times 32\) = 1.6 gm

Example 5: Calculate mass of Na₂SO₄ obtained when
100 ml of 0.2 M H₂SO₄ is completely neutralised by NaOH.
Solution: Mole of H₂SO₄ taken =
Molarity  × Vol. (lit) = \(\frac { 100 }{ 1000 } \times 0.2\) = 0.02
H₂SO₄       +        2NaOH  →  Na₂SO₄     +   2H₂O
(0.02 mole)                              (0.02 mole)
Mole of Na₂SO₄ obtained = 0.02
mass of Na₂SO₄ = 0.02 × 142 = 2.84 gm