Refraction Of Light Through A Glass Slab

Refraction through a rectangular glass slab and principle of reversibility of light:
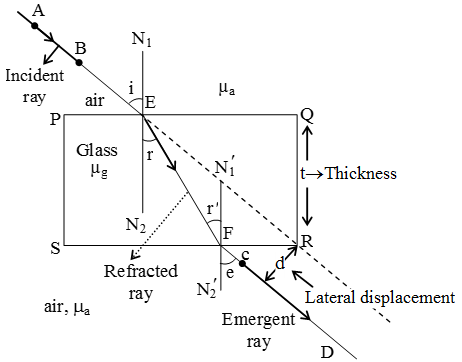
Consider a rectangular glass slab, as shown in figure. A ray AE is incident on the face PQ at an angle of incidence i. On entering the glass slab, it bends towards normal and travels along EF at an angle of refraction r. The refracted ray EF is incident on face SR at an angle of incidence r’. The emerged ray FD bends away from the normal at an angle of refraction e.
Thus the emergent ray FD is parallel to the incident rays AE, but it has been laterally displaced with respect to the incident ray. There is shift in the path of light on emerging from a refracting medium with parallel faces.
People also ask
- What is Refraction of Light?
- Analysing Refraction of Waves
- Examples of refraction of light
- What is the index of refraction?
- What is atmospheric refraction?
Lateral shift:
Lateral shift is the perpendicular distance between the incident and emergent rays when light is incident obliquely on a refracting slab with parallel faces.
Factors on which lateral shift depends are:
(i) Lateral shift is directly proportional to the thickness of glass slab.
(ii) Lateral shift is directly proportional to the incident angle.
(iii) Lateral shift is directly proportional to the refractive index of glass slab.
(iv) Lateral shift is inversely proportional to the wavelength of incident light.
Proof for i = e
Case-I:
For light going from air to glass at point E.
µa sin i = µg sin r ….. (1)
Case-II:
For light going from glass to air at point F.
µg sin r = µa sin e ….. (2)
From (1) & (2) we can say that i = e
⇒ incident & emergent rays are parallel to each other.
