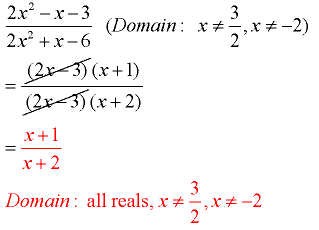Reducing Algebraic Fractions
Steps to Reducing Algebraic Fractions:
- Determine the domain of the expression, looking for zero denominator problems.
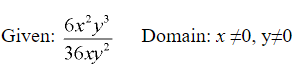
- Factor the numerator and denominator, looking for common factors.
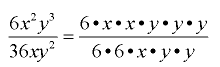
- Identify the factors of 1, and write the final simplified answer (what’s “left”).
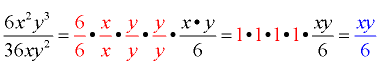
- State the domain of the simplified expression.
The domain of a simplified answer is always stated to be the same as the domain of the original expression. In this case, the domain remains “all real numbers, but not x = 0 and not y = 0”.
Monomial Fractions
If there is only one term (monomial) in the numerator and denominator, then common factors may be reduced directly.
Example:

Remember:
- There will always be a larger number (coefficient) “leftover” where there was a larger number “to begin with”.
- Similarly, there will be variables “leftover” where there were “more” (larger exponents) to begin with.
- The “leftover” variables are determined by subtracting their exponents.
Polynomial Fractions
If there is more than one term in either the numerator or denominator (or both), you may need to factor. Factoring will often allow for reducing, since factoring produces products and reducing can only occur when multiplication “connects” parts. You can never reduce part of a sum or part of a difference.
You cannot reduce part of a sum or part of a difference.
Example 1: (common factor)

Example 2: (factor perfect square)

Example 3: (factor trinomials, a = 1)

Example 4: (factor out -1)
When the “terms” in an expression are the same, but with opposite “signs”, factor out -1 from one of the expressions to obtain your common factor.

Example 5: (factor trinomials, a ≠ 1)