Ratios
- A ratio is a comparison of two quantities.A ratio of one number to another number is the quotient of the first number di
- vided by the second number. (Where the second number is not zero.)
- Ratios are most commonly written as a fraction.
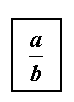
- A ratio can be written in a variety of ways.
- Since a ratio can be written as a fraction, it can also be written in any form that is equivalent to that fraction. All of the following are equivalent:
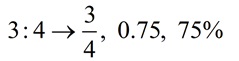
Notice that the order is important: 3 : 4 ≠ 4 : 3 because 3/4 ≠ 4/3. - Terms used with ratios:
Continued Ratio: (the comparison for more than two quantities) a : b : c
Equivalent Ratios: (all reduce to the same value)
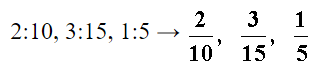
Hint: When working with ratios such as 2 : 3 : 5, use 2x, 3x, and 5x to write an equation!
Consider this situation: There are 16 girls and 14 boys in a math class.
Part-to-Part Comparison:
If we compare the number of girls to the number of boys, we obtain a ratio of 16 : 14 or 8 : 7
This is comparing one “part” of the class to another “part” of the class.
Part-to-Whole Comparison:
If we compare the number of girls to the total number of students, we obtain a ratio of 16 : 30 or 8 : 15
This is comparing one “part” of the class to the “whole” class.
It is always important to read questions carefully to determine if the ratio will be between “two parts” or between “one part and the whole”.
Example: A teacher graded 180 bonus quizzes during the school year. The number of quizzes receiving A’s, B’s, and C’s were in the ratio of 5 : 3 : 1, respectively. Find the number of bonus quizzes that received a grade of A for the school year.
Solution: Represent the number of each grade as 5x, 3x and 1x.
Since there were 180 bonus quizzes in total, we have:
5x + 3x + x = 180
9x = 180
x = 20
Since the 5x represents the number of A’s, substitute to find the final answer.
5(20) = 100
100 bonus quizzes received an A.
