Quadratic Equations

Quadratic Equations

An equation in which the highest power of the unknown quantity is two is called quadratic equation.

Types of quadratic equation

Quadratic equations are of two types:

Roots of a quadratic equation:
The values of variable x which satisfy the quadratic equation is called roots of quadratic equation.

Solution of quadratic equation

(1) Factorization method
Let ax² + bx + c = a(x – α)(x – β) = 0.
Then x = α and x = β will satisfy the given equation.
Hence, factorize the equation and equating each factor to zero gives roots of the equation.
Example: 3x² – 2x + 1 = 0 ⇒(x – 1)(3x + 1) = 0; x = 1, -1/3

(2) Sri Dharacharya method 
By completing the perfect square as

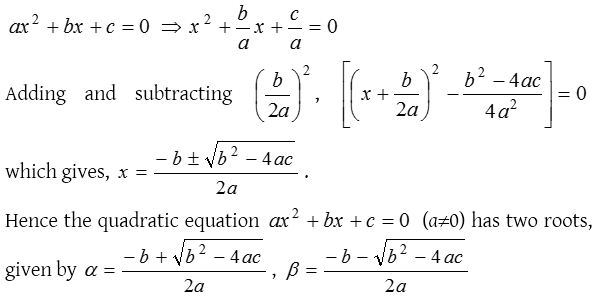
Every quadratic equation has two and only two roots.

https://www.youtube.com/watch?v=Nf1Fs8ln8tw

Nature of roots

In a quadratic equation ax² + bx + c = 0, let us suppose that are real and a ≠ 0. The following is true about the nature of its roots.

1. The equation has real and distinct roots if and only if D ≡ b² – 4ac > 0.
2. The equation has real and coincident (equal) roots if and only if D ≡ b² – 4ac = 0.
3. The equation has complex roots of the form α ± iβ, α ≠ 0 if and only if D ≡ b² – 4ac < 0.
4. The equation has rational roots if and only if a, b, c ∈ Q (the set of rational numbers) and D ≡ b² – 4ac is a perfect square (of a rational number).
5. The equation has (unequal) irrational (surd form) roots if and only if D ≡ b² – 4ac > 0 and not a perfect square even if a, b and c are rational. In this case if p + √q, p,q rational is an irrational root, then p – √q is also a root (a, b, c being rational).
6. α + iβ (β ≠ 0 and α, β ∈ R) is a root if and only if its conjugate α – iβ is a root, that is complex roots occur in pairs in a quadratic equation. In case the equation is satisfied by more than two complex numbers, then it reduces to an identity.
   0.x² + 0.x + 0 = 0, i.e., a = 0 = b = c.

Relations between roots and coefficients

(1) Relation between roots and coefficients of quadratic equation: If α and β are the roots of quadratic equation , (a ≠ 0) then

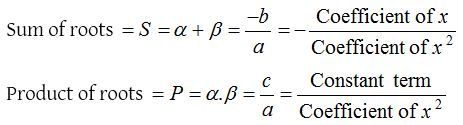
(2) Formation of an equation with given roots: A quadratic equation whose roots are α and β is given by (x – α)(x – β) = 0.
∴ x² – (α+iβ)x + αβ = 0
i.e. x² – (sum of roots)x + (product of roots) = 0
∴ x² – Sx + P = 0
(3) Symmetric function of the roots : A function of α and β is said to be a symmetric function, if it remains unchanged when α and β are interchanged.
For example, α² + β² + 2αβ is a symmetric function of α and β whereas α² + β² + 2αβ is not a symmetric function of α and β.
In order to find the value of a symmetric function of α and β, express the given function in terms of α + β and αβ. The following results may be useful.

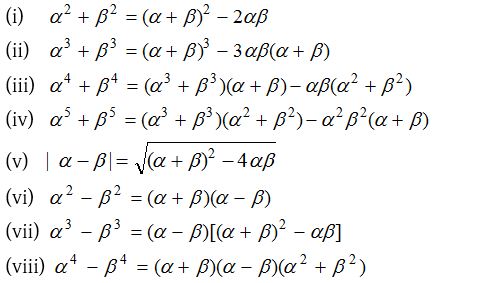
Properties of quadratic equation

1. If f(a) and f(b) are of opposite signs then at least one or in general odd number of roots of the equation lie between a and b.
2. If then f(a) = f(b) there exists a point c between a and b such that f(c) = 0, a<c<b.
3. If α is a root of the equation f(x) = 0 then the polynomial f(x) is exactly divisible by (x – α), then (x – α) is factor of f(x).
4. If the roots of the quadratic equations a₁x² + b₁x + c₁ = 0 and a₂x² + b₂x + c₂ = 0 are in the same ratio [i.e. α₁/β₁ = α₂/β₂] then b₁²/b₂² = a₁c₁/a₂c₂.