Pythagorean Identities
When studying the unit circle, it was observed that a point on the unit circle (the vertex of the right triangle) can be represented by the coordinates (cos θ, sinθ)
Since the legs of the right triangle in the unit circle have the values of and , the Pythagorean Theorem can be used to obtain
Sin2θ + Cos2θ = 1

This well-known equation is called a Pythagorean Identity.
The value of is immaterial.
Using this first Pythagorean Identity, two additional Pythagorean Identities can be created.


Examples:
The Pythagorean Identities may be used to find missing trigonometric values.

A more widely known use of the Pythagorean Identities is to help simplify trigonometric expressions.
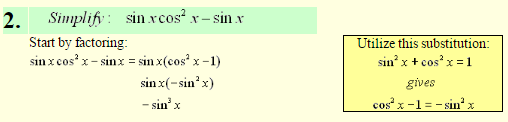
Pythagorean Identities are also helpful in simplifying trigonometric expressions to create a factorable expression.

Such processes, as seen here, will also prove valuable when solving trigonometric equations.
