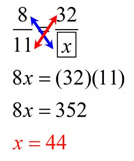Proportions
- A proportion is a comparison of ratios.
- A proportion is an equation that states that two ratios are equal, such as
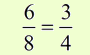
- Proportions always have an EQUAL sign!
- A proportion can be written in two ways:
In each proportion the first and last terms (4 and 2) are called the extremes. The second and third terms (8 and 1) are called the means.
| Determine if a Proportion is TRUE: You can tell if a simple proportion is true by just examining the fractions. If the fractions both reduce to the same value, the proportion is true. | 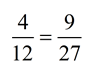 This is a true proportion, since both fractions reduce to 1/3. |
| Find a Missing Part (a Variable) in a Proportion: You can often use this same approach when solving for a missing part of a simple proportion. Remember that both fractions must represent the same value. Notice how we solve this problem by getting a common denominator for the two fractions. | 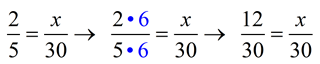 To find x, use the common denominator of 30. To change 5 to 30, multiply by 6. The SAME must be done to the top, (multiply 2 by 6) to keep the fractions equal. ANSWER: x = 12 |
This simple approach may not be sufficient when working with more complex proportions.
You need a rule:
Some people call this rule Cross Multiply!!
Universal Rule:
There is a rule (or algorithm) that can be followed to determine if two fractions are equal. The process multiplies from the top “across” to the bottom between the fractions in the proportion. If these products are equal, the fractions are equal. This method is very handy for setting up an equation to solve for a variable.
A more precise statement of the rule is:
RULE: In a true proportion, the product of the means equals the product of the extremes.
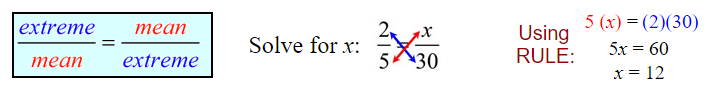
Proportions can also be solved by multiplying each side of the proportion by the common denominator for both fractions.
A proportion can be rewritten in different ways, yet remain true.
The following proportions are all equivalent (mathematically the same).
Check that this is true using “cross multiply”.
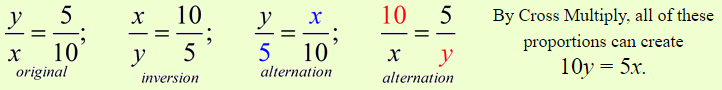
Example 1: Solve for x algebraically in this proportion:
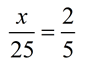Solution:
Example 2:
Solution:
Example 3: The length of a stadium is 100 yards and its width is 75 yards. If 1 inch represents 25 yards, what would be the dimensions of the stadium drawn on a sheet of paper?
Solution: This problem can be solved by an intuitive approach, such as:
100 yards by 75 yards
100 yards = 4 inches (HINT: 100 / 25)
75 yards = 3 inches (HINT: 75 / 25)
Therefore, the dimensions would be 4 inches by 3 inches.
Solution by proportion: (Notice that the inches are all on the top and the yards are all on the bottom for this solution. Other combinations are possible.)
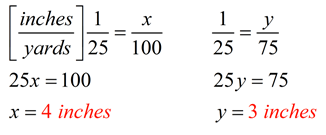
Example 4: The ratio of boys to girls in Spanish club is 4 to 5. If there are 25 girls in the club, how many boys are in the club?
Solution:
Method 1:
Use the common denominator of 25:
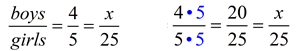
x = 20 means there are 20 boys in the club.
Method 2:
Using the rule:
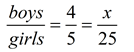
4•25 = 5•x
100 = 5x
x = 20 means there are 20 boys in the club.
Example 5: Find the missing term:
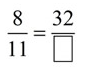
Solution:
Method 1:
Getting a common denominator is not as easy in
this problem as it was in Example 2. The common denominator will be 11x (where x represents the empty box). You can, in this problem, notice that
8 x 4 = 32. Multiplying the denominator by this same value will create a TRUE proportion: 11 x 4 gives the answer 44.
If you want to use 11x as the common denominator,
you will get:
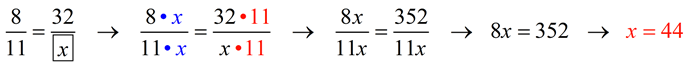
Method 2: (using RULE)
