Properties of Arithmetic, Geometric, Harmonic Means between Two Given Numbers
Let A, G and H be arithmetic, geometric and harmonic means of two numbers a and b.
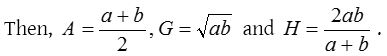
These three means possess the following properties :
(1) A ≥ G ≥ H
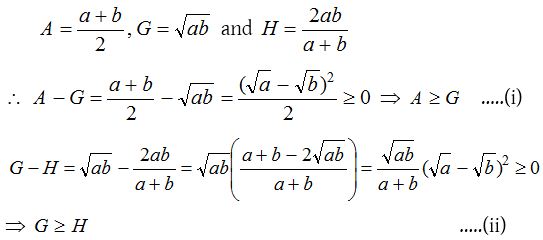
From (i) and (ii), we get A ≥ G ≥ H.
Note that the equality holds only when a = b.
(2) A, G, H from a G.P., i.e., G2 = AH
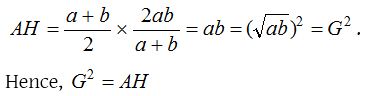
(3) The equation having a and b as its roots is
x2 – 2Ax + G2 = 0
The equation having a and b its roots is
x2 – (a + b)x + ab = 0
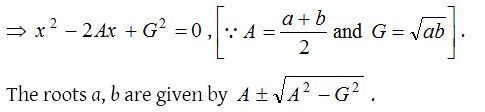
(4) If A, G, H are arithmetic, geometric and harmonic means between three given numbers a, b and c, then the equation having a, b, c as its roots is
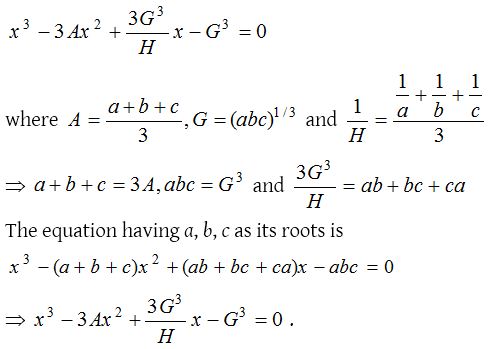
Relation between A.P., G.P. and H.P.
(1) If A, G, H be A.M., G.M., H.M. between a and b, then
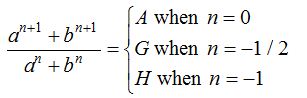
(2) If A1, A2 be two A.M.’s; G1, G2 be two G.M.’s and H1, H2 be two H.M.’s between two numbers a and b, then
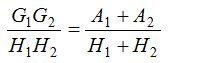
(3) Recognization of A.P., G.P., H.P. : If a, b, c are three successive terms of a sequence.
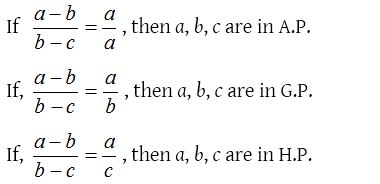
(4) If number of terms of any A.P./G.P./H.P. is odd, then A.M./G.M./H.M. of first and last terms is middle term of series.
(5) If number of terms of any A.P./G.P./H.P. is even, then A.M./G.M./H.M. of middle two terms is A.M./G.M./H.M. of first and last terms respectively.
(6) If pth, qth and rth terms of a G.P. are in G.P. Then p, q, r are in A.P.
(7) If a, b, c are in A.P. as well as in G.P. then a = b = c.
(8) If a, b, c are in A.P., then xa, xb, xc will be in G.P. x ≠ ±1.
