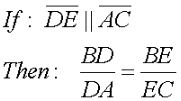Proofs with Similar Triangles
Definition:
Two triangles are similar if and only if the corresponding sides are in proportion and the corresponding angles are congruent.
There are three accepted methods of proving triangles similar:
AA
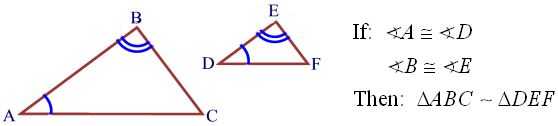
To show two triangles are similar, it is sufficient to show that two angles of one triangle are congruent (equal) to two angles of the other triangle.
Theorem:
If two angles of one triangle are congruent to two angles of another triangle, the triangles are similar.
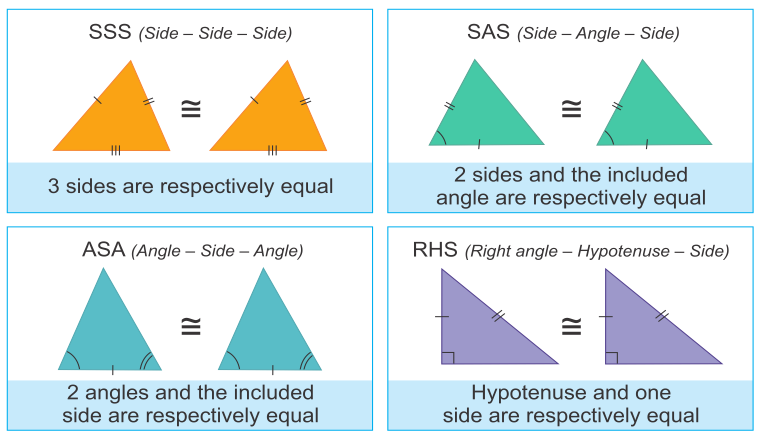
SSS for similarity
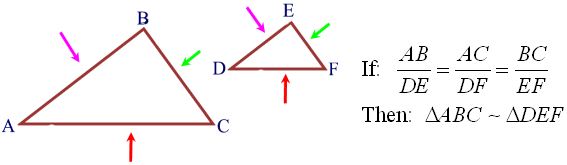
SSS for similar triangles is NOT the same theorem as we used for congruent triangles. To show triangles are similar, it is sufficient to show that the three sets of corresponding sides are in proportion.
Theorem:
If the three sets of corresponding sides of two triangles are in proportion, the triangles are similar.
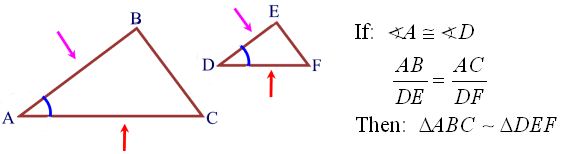
SAS for similarity
SAS for similar triangles is NOT the same theorem as we used for congruent triangles. To show triangles are similar, it is sufficient to show that two sets of corresponding sides are in proportion and the angles they include are congruent.
Theorem:
If an angle of one triangle is congruent to the corresponding angle of another triangle and the lengths of the sides including these angles are in proportion, the triangles are similar.
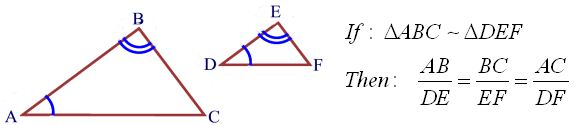
Once the triangles are similar:
Theorem:
The corresponding sides of similar triangles are in proportion.
Dealing with overlapping triangles:
Many problems involving similar triangles have one triangle ON TOP OF (overlapping) another triangle.
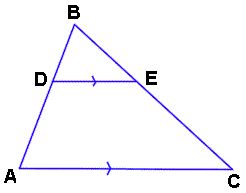Since \(\overline { DE }\) is marked to be parallel to \(\overline { AC }\), we know that we have ∠BDE congruent to ∠DAC (by corresponding angles). ∠B is shared by both triangles, so the two triangles are similar by AA.
There is an additional theorem that can be used when working with overlapping triangles:
Additional Theorem: If a line is parallel to one side of a triangle and intersects the other two sides of the triangle, the line divides these two sides proportionally.
