Probability Involving AND and OR
Let’s examine AND first:
In probability, an outcome is in event
“A and B” only when the outcome is in both event A and event B.
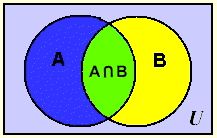 In Venn Diagrams, we learned that an element was in the intersection “A and B”, only when the element was in BOTH sets.
In Venn Diagrams, we learned that an element was in the intersection “A and B”, only when the element was in BOTH sets.
![]() n(A and B) means the number of outcomes in both A and B.
n(A and B) means the number of outcomes in both A and B.
n(S) means the total number of possible outcomes
Example:
A die is rolled. What is the probability that the number is even and less than 4?
Answer: Event A: Numbers on a die that are even: 2, 4, 6
Event B: Numbers on a die that are less than 4: 1, 2, 3
There is only one number (2) that is in both events A and B.
Total outcomes S: Numbers on a die: 1, 2, 3, 4, 5, 6 (total = 6)
Probability = 1/6
Let’s examine OR:
In probability, an outcome is in event “A or B” when the outcome is in either (or both) event A or event B.
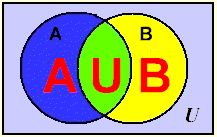 In Venn Diagrams, we learned that an element was in the union “A or B”, when the element was in either or both sets.
In Venn Diagrams, we learned that an element was in the union “A or B”, when the element was in either or both sets.
![]() The rule for OR takes into account those values that may get counted more than once when the probability is determined. Check out the example below.
The rule for OR takes into account those values that may get counted more than once when the probability is determined. Check out the example below.
Example:
A die is rolled. What is the probability that the number is even or less than 4?
Event A: Numbers on a die that are even: 2, 4, 6 P(A)=3/6
Event B: Numbers on a die that are less than 4: 1, 2, 3 P(B)=3/6
P(A and B) = 1/6 (see rule above)
Answer: Probability = P(A) + P(B) – P(A and B)
= 3/6 + 3/6 – 1/6 = 5/6
Notice in this problem that the number 2 appears in both event A and event B. If we did not subtract the P(A and B), the answer would be 1 – which we know is not true since the number 5 appears in neither event.
