Positive, Negative, & Zero Exponents

As you know, exponents can be positive numbers, negative numbers, or zero.Let’s take a closer look at how to deal with exponents.Remember the rule for dividing like variables raised to a power?



Laws of Exponents


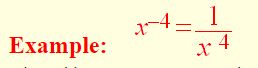
Remember: an expression with a negative power ends up on the opposite side
of the fraction bar as a positive power.


![]()
(The above rule is based on division. Since we cannot divide by a zero quantity, we must add the condition that .)
Example 1
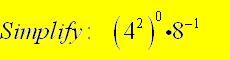
Solution
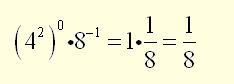
Example 2

Solution
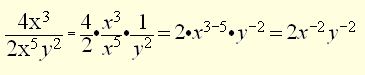
(In this problem, we have used negative powers to move the y variable to the numerator and to combine the x values. This is not the only way to express the answer.)
Example 3
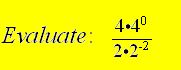
Solution
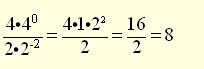
(The 2 raised to the negative power moves to the numerator with a positive power. Notice that the 0 power only affects the 4 which is raised to that power. It does not affect the multiple of 4.)
Example 4
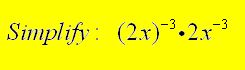
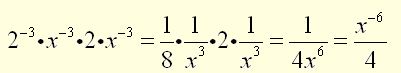
Notice how the parentheses affects the power of -3. If the power is outside the parentheses, all of the elements within the parentheses are affected, as in the first part of the problem. If there are no parentheses, as in the last part of the problem, the power affects only the term to which it is assigned (attached).)
Example 5
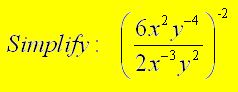
Solutions

(When solving these problems, it is usually easier to simplify inside the parentheses first.
Then deal with the outside exponent. Did you notice that the last step shows the negative
powers expressed as positive powers on the opposite side of the fraction bar?)
