Polynomials
Algebraic expression containing many terms of the form axn, n being a non-negative integer is called a polynomial. i.e., f(x) = a0 + a1x + a2x2 + a3x3 + …….. + an-1xn-1 + anxn, where x is a variable, a0, a1, a2, …… an are constants and an ≠ 0.
Example: 4x4 + 3x3 – 7x2 + 5x + 3, 3x3 + x2 – 3x + 5.
(1) Real polynomial:
f(x) = a0 + a1x + a2x2 + a3x3 + …….. + anxn is called real polynomial of real variable x with real coefficients.
Example: 3x3 – 4x2 + 5x – 4, x2 – 2x + 1 etc. are real polynomials.
(2) Complex polynomial:
f(x) = a0 + a1x + a2x2 + a3x3 + …….. + anxn is called complex polynomial of complex variable x with complex coefficients.
Example: 3x2 – (2+4i)x + (5i-4), x3 – 5ix2 + (1+2i)x + 4 etc. are complex polynomials.
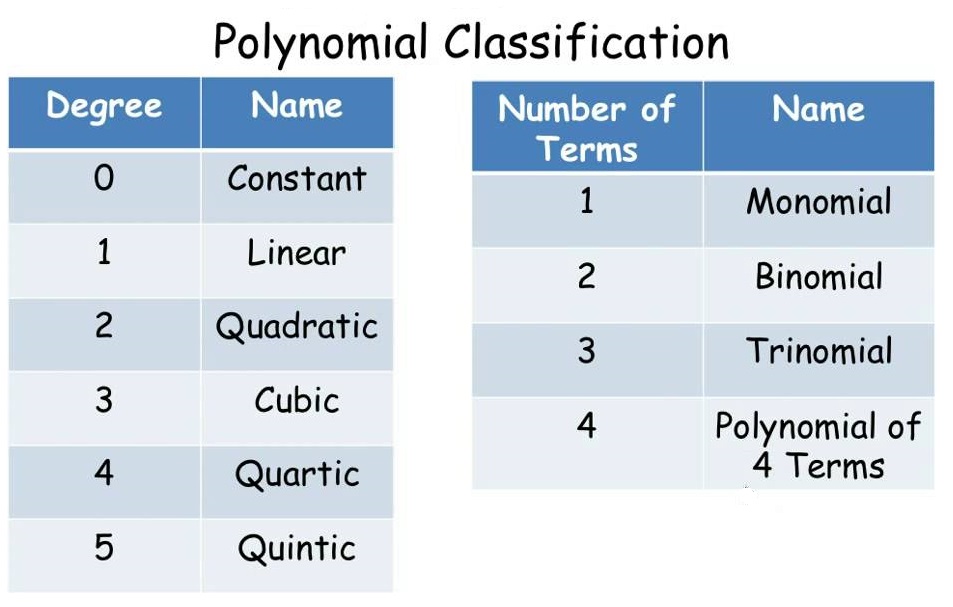
(3) Degree of polynomial:
Highest power of variable x in a polynomial is called degree of polynomial.
Example: f(x) = a0 + a1x + a2x2 + a3x3 + …….. + anxn is a n degree polynomial.
f(x) = 4x3 + 3x2 – 7x + 5 is a 3 degree polynomial.
A polynomial of second degree is generally called a quadratic polynomial. Polynomials of degree 3 and 4 are known as cubic and biquadratic polynomials respectively.
(4) Polynomial equation:
If f(x) is a polynomial, real or complex, then f(x) = 0 is called a polynomial equation.
Read More:
- What is a Polynomial?
- Types of Polynomials
- Monomials, Binomials, and Polynomials
- Adding Polynomials
- Subtracting Polynomials
- Dividing Polynomials
- Polynomials – Long Division
- Degree (of an Expression)
- Special Binomial Products
- Multiplying Binomials
- Difference of Two Cubes
- Polynomial Remainder Theorem
- Factoring in Algebra
- Factorization of Polynomials Using Factor Theorem
- How do you use the factor theorem?
- How to factorise a polynomial by splitting the middle term?
- Review Factoring Polynomials
- Zeros of a Polynomial Function
- Factors and Coefficients of a Polynomial
- Roots of Polynomials: Sums and Products
- Solving Polynomial Equations of Higher Degree
- Examining Graphs of Polynomial Equations of Higher Degree
