Point-Slope Equation of a Line
Equations of straight line in different forms
(1) Slope form:
Equation of a line through the origin and having slope m is y = mx.
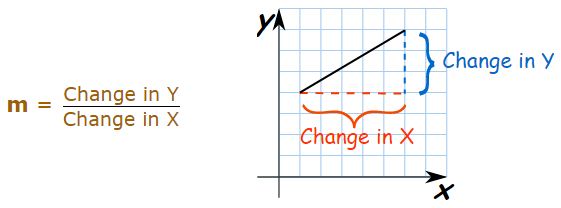 (2) One point form or Point slope form:
(2) One point form or Point slope form:
Equation of a line through the point (x1, y1) and having slope m is y − y1 = m(x − x1).
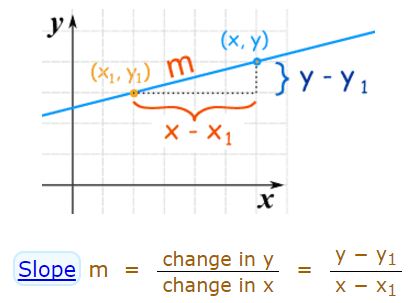 (3) Slope intercept form:
(3) Slope intercept form:
Equation of a line (non-vertical) with slope m and cutting off an intercept c on the y-axis is y = mx + c.
 The equation of a line with slope m and the x-intercept d is y = m(x − d).
The equation of a line with slope m and the x-intercept d is y = m(x − d).
(4) Intercept form:
If a straight line cuts x-axis at A and the y-axis at B then OA and OB are known as the intercepts of the line on x-axis and y-axis respectively.
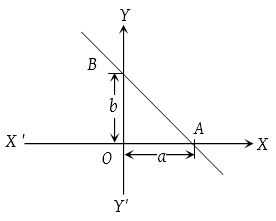 Then, equation of a straight line cutting off intercepts a and b on x–axis and y–axis respectively is xa+yb=1xa+yb=1.
Then, equation of a straight line cutting off intercepts a and b on x–axis and y–axis respectively is xa+yb=1xa+yb=1.
If given line is parallel to X axis, then X-intercept is undefined.
If given line is parallel to Y axis, then Y-intercept is undefined.
(5) Two point form:
Equation of the line through the points A(x1, y1) and B(x2, y2) is, (y−y1)=y2−y1x2−x1(x−x1)(y−y1)=y2−y1x2−x1(x−x1).
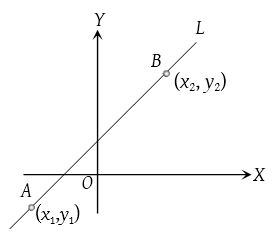 In the determinant form it is gives as |xy1x1y11x2y21|=0 is the equation of line.
In the determinant form it is gives as |xy1x1y11x2y21|=0 is the equation of line.
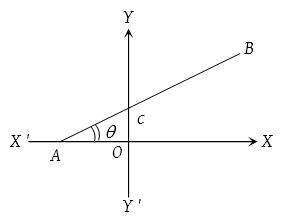
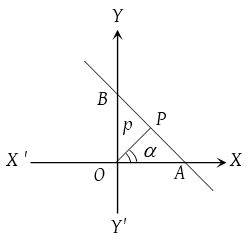
(6) Normal or perpendicular form:
The equation of the straight line upon which the length of the perpendicular from the origin is p and this perpendicular makes an angle α with x-axis is x cos α + y sin α = p.
 (7) Symmetrical or parametric or distance form of the line:
(7) Symmetrical or parametric or distance form of the line:
Equation of a line passing through (x1, y1) and making an angle θ with the positive direction of x-axis is ,
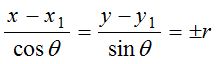
where r is the distance between the point P(x, y) and A(x1, y1).
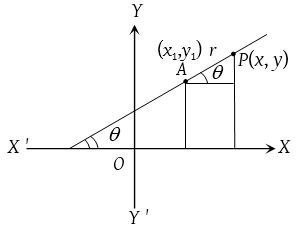 The co-ordinates of any point on this line may be taken as (x1 ± r cos θ, y1 ± r sin θ), known as parametric co-ordinates. ‘r’ is called the parameter.
The co-ordinates of any point on this line may be taken as (x1 ± r cos θ, y1 ± r sin θ), known as parametric co-ordinates. ‘r’ is called the parameter.
