Kerala Plus Two Maths Previous Year Question Paper March 2018 with Answers
| Board | SCERT |
| Class | Plus Two |
| Subject | Maths |
| Category | Plus Two Previous Year Question Papers |
Time : 2½ Hours
Cool off time : 15 Minutes
Maximum : 80 Score
General Instructions to Candidates :
- There is a ‘Cool off time’ of 15 minutes in addition to the writing time.
- Use the ‘Cool off time’ to get familiar with questions and to plan your answers.
- Read questions carefully before you answering.
- Read the instructions carefully.
- When you select a question, all the sub-questions must be answered from the same question itself.
- Calculations, figures and graphs should be shown in the answer sheet itself.
- Malayalam version of the questions is also provided.
- Give equations wherever necessary.
- Electronic devices except non programmable calculators are not allowed in the Examination Hall.
Question 1 to 7 carry 3 scores each. Answer any six questions. (6 × 3 = 18)
Question 1.
If f(x) = xx−1, x ≠ 1
i) Find fof (x)
ii) Find the inverse of f.
Answer:
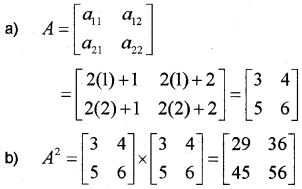
Question 2.
Using elementary row operations, find the inverse of the matrix [122−1]
Answer:
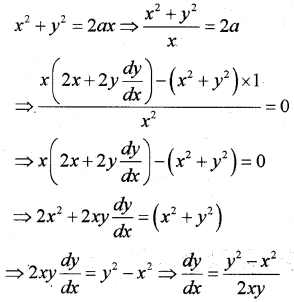
Question 3.
i) f(x) is a strictly increasing function, if f'(x) is ………..
a) positive
b) negative
c) 0
d) None of these,
ii) Show that the function f given by f(x) = x3 – 3x2 + 4x, x ∈ R is strictly increasing.
Answer:
i) a) Positive.
ii) f(x) = x3 – 3x2 + 4x
= 3 (x2 – 2x + 1 – 1 + 43) = 3((x + 1)2 + 13) > 0
Question 4.
i) ∫a0f(a – x)dx = …………
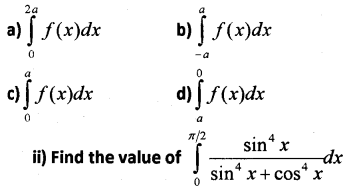
Answer:
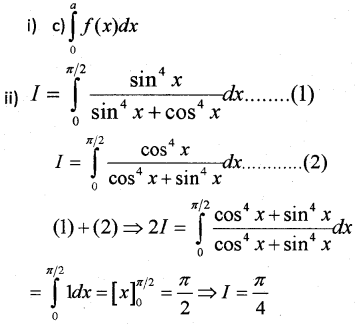
Question 5.
Find the area of the region bounded by the curve y2 = x’, x-axis and the lines x = 1 and x = 4.
Answer:
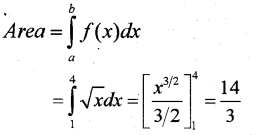
Question 6.
Find the general solution of the differential equation x dydx + 2y = x2 log x
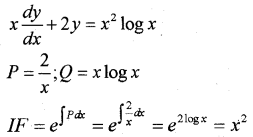
Solution is
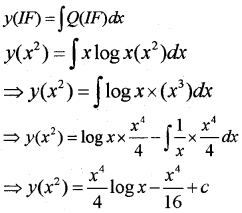
Question 7.
A manufacturer produces nuts and bolts. It takes 1 hour of work on Machine A and 3 hours on Machine B to produce a package of nuts. It takes 3 hours on Machine A and 1 hour on Machine B to produce a package of bolts. He earns profit of Rs. 17.50 per package on nuts and Rs. 7.00 per package on bolts. Formulate the above LPp if the Machine operates for at most 12 hours a day.
Answer:
Let x packet of nuts and y packets of bolts.
Maximise: Z=17. 5x + 7y
Subject to
x + 3y ≤ 12; 3x + y ≤ 12; x, y ≥ O
Questions 8 to 17 carry 4 scores each. Answer any 8. (8 × 4 = 32)
Question 8.
Let A = N × N and ‘*’ be a binary operation on A defined by
(a, b)*(c, d)=(a + c, b + d)
i) Find (1, 2) * (2, 3)
ii) Prove that * is commutative.
iii) Prove that * is associative.
Answer:
i) (1, 2)*(2, 3)=(1 + 2, 2 + 3) = (3, 5)
ii) (c, d)*(a, b) = (c + a, d + b)
= (a + c, b + d) = (a, b)* (c, d)
iii) (a, b)*[(c, d)*(e, f)] = (a, b)*(c + e, d + f)
= (a + c + e, b + d + f)
[(a, b) * (c, d)] * (e, f) = (a + c, b + d) * (e, f)
= (a + c + e, b + d + f)
Question 9.
i) Identify the function from the above graph
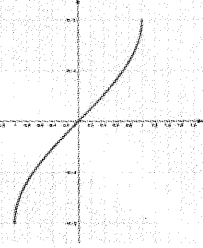
a) tan-1x
b) sin-1x
c) cos-1x
d) cos ec-1x
ii) Find the domain and range of the function represented in above graph.
iii) Prove that tan−112+tan−1211=tan−134
Answer:
i) sin-1x
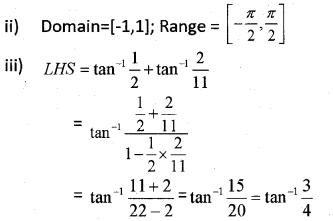
Question 10.
i) d(ax)dx = ………..
a) ax
b) log(ax)
c) ax log a
d) xax-1
ii) Find dydx if xy = yx
Answer:
i) ax loga
ii) Given; yx = xy, taking log on both sides;
x log y = y log x,
Differentiating with respect to x;
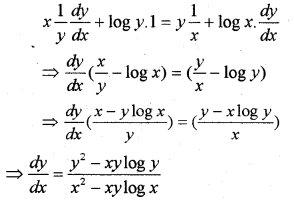
Question 11.
i) Find the slope of the tangent to the curve y = (x – 2)2 at x = 1.
ii) Find a point at which the tangent to the curve y = (x – 2)2 is parallel to the chord joining the point A (2, 0) and B (4, 4)
iii) Find the equation of the tangent to the above curve and parallel to the line AB.
y2 = 4ax, a > 0 and x2 = 4ay, a > 0
Answer:
i) dydx = 2(x – 2) ⇒ Slope = 2(1 – 2) = -2
ii) Slope of AB = y2−y1x2−x1=4−04−2=2
Here 2(x – 2) = 2 ⇒ x = 3, y = 1
iii) Equation of the tangent line is
y – 1 = 2 (x – 3) ⇒ 2x – y = 5
Question 12.
∫20(x2 +1)dx as the limit of a sum.
Answer:
Here; f(x) = x2 + 1; a = 0, b = 2 ⇒ h = 2n
∫20(x2 +1)dx
lim h[f(0) + f(0 + h) + f(0 + 2h)+…+ f(0 + (n – 1)h)]
\lim _{h \rightarrow 0} h (1 + (h2 + 1)+((2h) 2 + 1)+…+[(n – 1)h2] + 1]
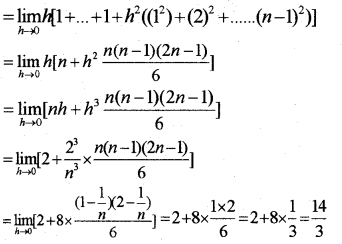
Question 13.
Consider the following figure:
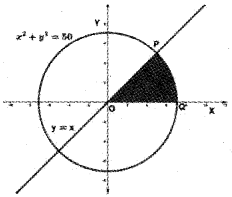
i) Find the point of intersection ‘P’ of the circle x2 + y2 = 50 and the line y = x
ii) Find the area of the shaded region.
Answer:
i) point of intersection is x2 + x2 = 50 ⇒ x2 = 25 ⇒ ±5; y = ±5
point P is (5, 5)
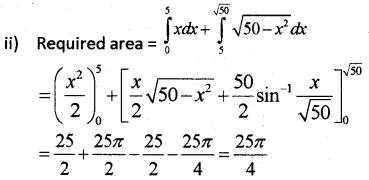
Question 14.
i) The degree of the differential equation x y\left(\frac{d^{2} y}{d x^{2}}\right)^{2}+x^{4}\left(\frac{d y}{d x}\right)^{3}-y \frac{d y}{d x}=0 is ………
a) 4
b)3
c)2
d)1
ii) Find the general solution of the differential equation
sec2 x tan ydx + sec2 y tan xdy = 0
Answer:
i) c
ii) Given; sec2x tan ydx + sec2y tan xdy = 0
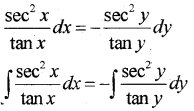
log tanx = -log tany + c
log tan x + log tan y = c
Question 15.
i) Prove that for any vector \bar{a}, \bar{b}, \bar{c}
[\bar{a}+\bar{b}, \bar{b}+\bar{c}, \bar{c}+\bar{a}]=2\left[\begin{array}{lll} \bar{a} & \bar{b} & \bar{c} \end{array}\right]
ii) Show that if \bar{a}+\bar{b}, \bar{b}+\bar{c}, \bar{c}+\bar{a} are coplanar then \bar{a}, \bar{b}, \bar{c} are also coplanar.
Answer:

Question 16.
i) Find the equation of a plane which makes x,y,z intercepts respectively as 1, 2, 3.
ii) Find the equation of a plane passing through the point (1, 2, 3) which is parallel to above plane.
Answer:
\frac{x}{1}+\frac{y}{2}+\frac{z}{3} ⇒ 6x + 3y + 2z = 6
ii) Equation of the parallel plane passing
6(x – 1) + 3( y – 2) + 2(z – 3) = 0
⇒ 6x + 3y + 2z – 18 = 0
Question 17.
Solve the LPP graphically:
Minimise z = -3x + 4y
Subject to constraints:
x + 2y ≤ 8; 3x + 2y ≥ l2; x, y ≥ 0
Answer:
x + 2y = 8
| X | 0 | 8 |
| Y | 4 | 0 |
3x + 12y = 12
| X | 0 | 4 |
| Y | 6 | 0 |
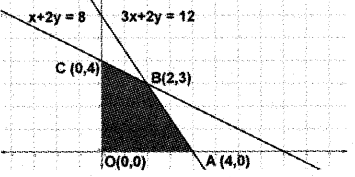
The corner points are O(0, 0), A(4, 0), B(2, 3), C(0, 4)
| Corner point | Z = -3x + 4y |
| O(0, 0) | Z = 0 + 0 = 0 |
| A(4, 0) | Z = -12 + 0 = -12 |
| B(2, 3) | Z = -6 + 12 = 6 |
| C(0, 4) | Z = 0 + 16 = 16 |
Z attains minimum at (4,0).
Questions from 18 to 24 carry 6 scores each. Answer any 5. (5 × 6 = 30)
Question 18.
i) Find x and y if x\left[\begin{array}{l} 2 \\ 3 \end{array}\right]+y\left[\begin{array}{c} -1 \\ 1 \end{array}\right]=\left[\begin{array}{c} 10 \\ 5 \end{array}\right]
ii) Express the matrix \left[\begin{array}{ccc} 2 & -2 & -4 \\ -1 & 3 & 4 \\ 1 & -2 & -3 \end{array}\right] as the sum of a symmetric and a skew symmetric matrices.
Answer:
Given; 2x – y = 10; 3x + y = 5
5x = 15 ⇒ x = 3; y = -4
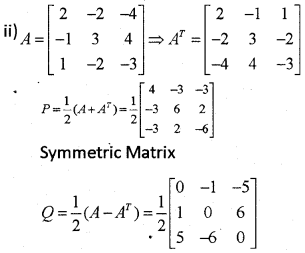
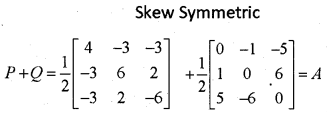
Question 19.
i) Prove that \left|\begin{array}{ccc} a & b & c \\ a+2 x & b+2 y & c+2 z \\ x & y & z \end{array}\right|=0
ii) If A = \left[\begin{array}{ccc} 1 & -1 & 2 \\ 0 & 2 & -3 \\ 3 & -2 & 4 \end{array}\right], B = \left[\begin{array}{ccc} -2 & 0 & 1 \\ 9 & 2 & -3 \\ 6 & 1 & -2 \end{array}\right]
a) Prove that B = A-1
b) Using Asolve the system of linear equations given below:
x – y + 2z = 1; 2y – 3z = 1; 3x – 2y + 4z = 2
Answer:
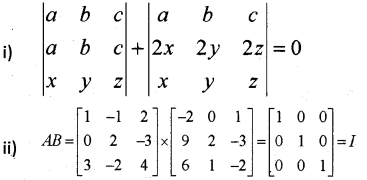
iii) Matrix form of the system of linear equation is
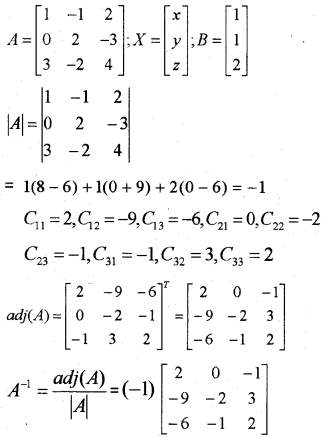
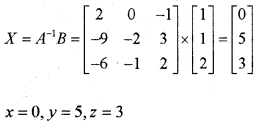
Question 20.
i) Prove that the function defined by f(x) = cos x2 is a continuous function.
ii) a) If y = e^{a \cos ^{-1} x}, -1 ≤ x ≤ 1, show that
\frac{d y}{d x}=\frac{-a e^{a \cos ^{-1} x}}{\sqrt{1-x^{2}}}
b) Hence prove that
\left(1-x^{2}\right) \frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}-a^{2} y=0
Answer:
i) f(x) = cosx; g(x) = x2 both are continuous.
Composition two continuous function is again continuous.
fog(x) = f(g(x)) = cos(x2)
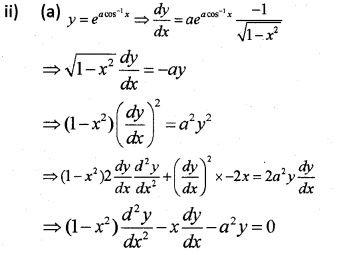
Question 21.
Evaluate the following:
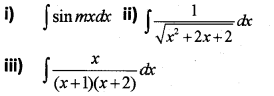
Answer:
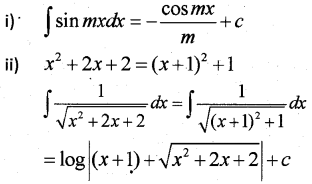
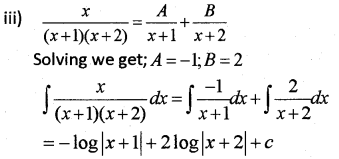
Question 22.
i) lf \bar{a} = 3i + 2j + 2k, \bar{b} = i + 2j – 2k
a) Find \bar{a} + \bar{b}, \bar{a} – \bar{b}
b) Find a unit vector perpendicular to both \bar{a} + \bar{b}, \bar{a} – \bar{b}
ii) Consider the points A(1, 2, 7); B(2, 6, 3); C (3, 10, -1)
a) Find \overline{A B}, \overline{B C}
b) Prove that A, B, C are collinear points.
Answer:
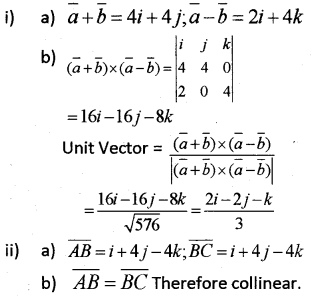
Question 23.
i) Find the angle between the lines \frac{x-2}{2}=\frac{y-1}{5}=\frac{z+3}{-3} and \frac{x+2}{-1}=\frac{y-4}{8}=\frac{z-5}{4}
ii) Find the shortest distance between the pair of lines
\bar{r} = (i + 2j + 3k) + λ(i – 3j + 2k)
\bar{r} = (4i + 5j +6k) + μ(2i + 3j + k)
Answer:
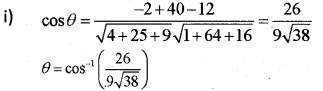

Question 24.
i) The probability distribution of a random variable is given by P(x). What is Σp(x)?
ii) The following is a probability distribution function of a random variable.
| X | -5 | -4 | -3 | -2 | -1 | 0 |
| P(x) | k | 2k | 3k | 4k | 5k | 7k |
| X | 1 | 2 | 3 | 4 | 5 | |
| P(x) | 8k | 9k | 10k | 11k | 12k |
a) Find k
b) P(x > 3)
c) P(-3 < x < 4)
d) P(x < -3)
Answer:
Σp(x) = 1
ii) a) k + 2k + 3k + 4k + 5k + 7k
+ 8k + 9k + 10k + 11k + 12k = 1
72k = 1 ⇒ k = \frac{1}{72}
b) P(x > 3) = P(4) + P(5) = 23k = \frac{23}{72}
c) P(-3 < x < 4) = P(-2) + P(-1) + P(0) + P(1) + P > (2)+ P > (3) = 43k = \frac{43}{72}
d) P(x < -3) = P(-5) + P(-4) = 3k = \frac{3}{72}
