Plus Two Maths Notes Chapter 2 Inverse Trigonometric Functions is part of Plus Two Maths Notes. Here we have given Plus Two Maths Notes Chapter 2 Inverse Trigonometric Functions.
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus Two |
| Subject | Maths Notes |
| Chapter | Chapter 2 |
| Chapter Name | Inverse Trigonometric Functions |
| Category | Kerala Plus Two |
Kerala Plus Two Maths Notes Chapter 2 Inverse Trigonometric Functions
Introduction
Trigonometric functions are real functions which are not objective and thus its inverse does not exist. In this chapter we study about the restrictions on domains and ranges of trigonometric functions which ensure the existence of their inverse and observe its graphical peculiarities.
A. Concepts
I. Functions
sin-1 x : [-1, 1 ] → [-π2, π2]
cos-1 x: [-1, 1] → [0, π]
tan-1 x : R → (−π2,π2)
cosec-1 x : R – (-1, 1) → [-π2, π2] – {0}
sec-1 x : R -(-1, 1) → [0, π] – {π2}
cot-1 x : R → (0, π)
II. Properties
1. sin (sin-1 x) = x, x ∈ [-1, 1]
sin-1(sinx) = x, x ∈ [-π2, π2]
cos(cos-1 x) = x, x ∈ [-1, 1]
cos-1(cosx) = x, x ∈ [o, π]
tan(tan-1 x) = x, x ∈ R
tan-1(tan x) = x, x ∈ (−π2,π2)
2. sin-1(-x) = -sin-1(x), x ∈ [-1, 1]
tan-1(-x) = -tan-1(x), x ∈ R
cosec-1(-x) = -cosec-1(x), x ∈ R -(-1, 1)
cos-1(-x) = π – cos-1(x), x ∈ [-1, 1]
cot-1(-x) = π – cot-1(x), x ∈ R
sec-1(-x) = π – sec-1(x), x ∈ R -(-1, 1)
sin-1(x) + cos-1(x) = π2, x ∈ [-1, 1].
3. cosec-1(x) + sec-1(x) = π2, |x| ≥ 1
tan-1(x) + cot-1(x) = π2, x ∈ R
4. sin-1 x
![]()
5. cos-1 x
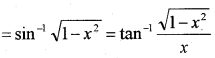
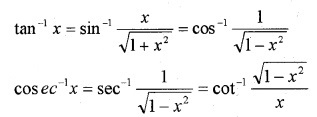
6. tan-1(x) + tan-1(y) =
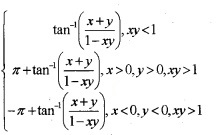
7. tan-1(x) – tan-1(y) =
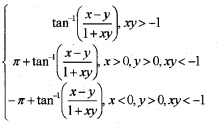
8. 2 tan-1 x
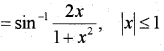
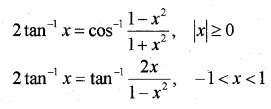
9. sin-1 x ± sin-1 y
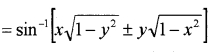
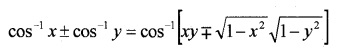
We hope the Kerala Plus Two Maths Notes Chapter 2 Inverse Trigonometric Functions help you. If you have any query regarding Kerala Plus Two Maths Notes Chapter 2 Inverse Trigonometric Functions, drop a comment below and we will get back to you at the earliest.
