Plus Two Maths Chapter Wise Questions and Answers Chapter 9 Differential Equations are part of Plus Two Maths Chapter Wise Questions and Answers. Here we have given Plus Two Maths Chapter Wise Questions and Answers Chapter 9 Differential Equations.
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus Two |
| Subject | Maths Chapter Wise Questions |
| Chapter | Chapter 9 |
| Chapter Name | Differential Equations |
| Number of Questions Solved | 50 |
| Category | Kerala Plus Two |
Kerala Plus Two Maths Chapter Wise Questions and Answers Chapter 9 Differential Equations
Plus Two Maths Differential Equations Three Mark Questions and Answers
Question 1.
y = e2x(a + bx), a and b are arbitrary constants.
Answer:
y = e2x(a + bx) ____(1)
Differentiating with respect to x,
\(\frac{d y}{d x}\) = e2xb + (a + bx)2e2x
\(\frac{d y}{d x}\) = 2y + be2x ⇒ \(\frac{d y}{d x}\) – 2y = be2x ____(2)
Differentiating (2) with respect to x,
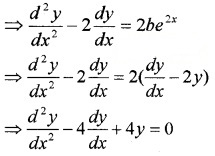
Question 2.
y = ex(acosx + 6sinx), a and b are arbitrary constants.
Answer:
y = ex(acosx + 6sinx) ___(1)
Differentiating with respect to x,
\(\frac{d y}{d x}\) = ex(-asinx + bcosx) + ex(acosx + bsinx) \(\frac{d y}{d x}\) = ex(-asin x + b cos x) + y
\(\frac{d y}{d x}\) – y = ex(-a sin x + b cos x) ____(2)
Differentiating (2) with respec to x,
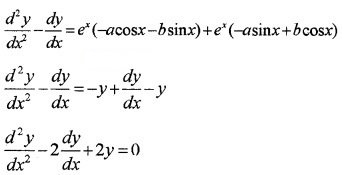
Question 3.
y = c1ex + c2 e-x , c1 and c1 are arbitrary constants.
Answer:
y = c1ex + c2 e-x ___(1)
Differentiating with respect to x,
\(\frac{d y}{d x}\) = c1ex + c2 e-x __(2)
Differentiating (2) with respect to x,
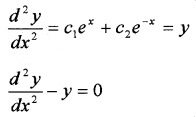
Question 4.
(x – a)2 + 2y2 = a2, a is a arbitrary constants.
Answer:
(x – a)2 + 2y2 = a2 ___(1)
Differentiating with respect to x,
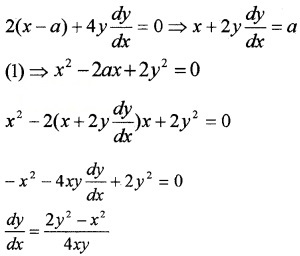
Question 5.
Find the equation of a curve passing through the point (0, -2) given that at any point (x, y) on the curve, the product of the slope of its tangent and y coordinate of the point is equal to the x coordinate of the point.
Answer:
y\(\frac{d y}{d x}\) = x ⇒ ydy = xdx
Integrating on both sides,
∫ydy = ∫xdx + c
⇒ \(\frac{y^{2}}{2}=\frac{x^{2}}{2}\) + c ____(1)
Since it passes through (0, -2),
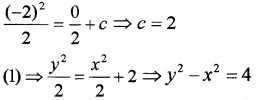
Question 6.
Form the DE representing the family of parabolas having a vertex at origin and axis along positive direction of x-axis.
Answer:
Let (a, 0) be focus of the given family of parabolas.
y2 = 4ax ____(1)
Differentiating with respect to x,
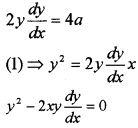
Question 7.
For the DE xy \(\frac{d y}{d x}\) = (x + 2)(y + 2), find the solution curve passing through the point(1,- 1).
Answer:
xy \(\frac{d y}{d x}\) = (x + 2)(y + 2)
⇒ \(\frac{y}{y+2} d x=\frac{x+2}{x} d x\)
Integrating on both sides,
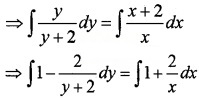
⇒ y – 2 log|y + 2| = x + 2log|x| + c ____(1)
Since it passes through (1, -1),
⇒ -1 – 2log|-1 + 2| = 1 + 2log|l| + c
⇒ -2 = c
(1) ⇒ y – 2log|y + 2| = x + 2log|x| – 2.
Question 8.
Solve the initial value problem: \(\frac{d y}{d x}\) = y tan 2x; y(0) = 2.
Answer:
\(\frac{d y}{d x}\) = y tan 2x
⇒ \(\frac{d y}{y}\) tan 2xdx,
This is a variable type
∴∫\(\frac{d y}{y}\) = ∫tan 2xdx ⇒ log y = \(\frac{1}{2}\) log|sec 2x| + c
Given y(0) = 2 ⇒ log 2 = \(\frac{1}{2}\) log|sec 0| + c ⇒ c = log 2
log y = \(\frac{1}{2}\) log|sec 2x| + log 2 ⇒
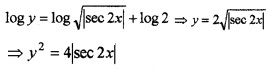
Plus Two Maths Differential Equations Four Mark Questions and Answers
Question 1.
(i) Consider the differential equation given below. (1)
\(\frac{d^{4} y}{d x^{4}}-\sin \left(\frac{d^{3} y}{d x^{3}}\right)=0\). Write the order and degree of the DE (if defined)
(ii) Find the Differential equation satisfying the family of curves y2 = a(b2 – x2), a and b are arbitrary constants. (3)
Answer:
(i) 4; degree is not defined
(ii) y2 = a(b2 – x2) ____(1)
Differentiating with respect to x,
2y \(\frac{d y}{d x}\) = -a2x ⇒ y\(\frac{d y}{d x}\) = -ax ____(2)
Differentiating (2) with respect to x,
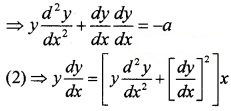
Which is the differential equation.
Question 2.
- Find the Differential equation satisfying the family of curves y = ae3x + be-2x, a and b are arbitrary constants. (3)
- Hence write the degree and order of the DE. (1)
Answer:
1. y = ae3x + be-2x ____(1)
Differentiating with respect to x,
\(\frac{d y}{d x}\) = ae3x × 3 + be-2x × -2 ____(2)
Differentiating (2) with respect to x,
⇒ \(\frac{d^{2} y}{d x^{2}}\) = 9ae3x + 4be-2x ____(3)
Now, (3) + 2 × (2) ⇒ \(\frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=15 a e^{3 x}\)
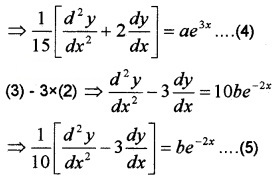
Using (4), (5) in (1), we have,
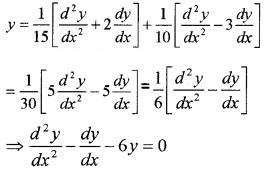
2. Order: 2; degree: 1.
Question 3.
Consider the equation of all circles which pass through the origin and whose centres are on the x-axis.
- Define the general equation of the circle.(1)
- Find the DE corresponding to the above equation. (3)
Answer:
1. The general equation of the circle, passing through the origin and whose centers lies on x-axis can be taken as (x – h)2 + y2 = h2 where h being an arbitrary constant.
2. Simplifying (x – h)2 + y2 = h2 we get,
x2 – 2hx + h2 + y2 = h2 ⇒ x2 – 2hx + h2 = 0 _____(1)
Differentiating we get,
2x + 2y \(\frac{d y}{d x}\) – 2h = 0 ⇒ h = x + y \(\frac{d y}{d x}\)
Substituting in (1) we can eliminate h
Question 4.
Find a particular solution satisfying the given condition. (x3 + x2 + x +1)\(\frac{d y}{d x}\) = 2x2 + x, y = 1, when x = 0.
Answer:
Integrating on both sides,
∫dy = ∫\(\frac{2 x^{2}+x}{\left(x^{2}+1\right)(x+1)} d x\)
Splitting into partial fractions we have, (see Unit:7)
Question 5.
- Write the degree of the DE y’ = 2xy. [0, 1, 2, 3] (1)
- Express y’ = 2xy in the form Mdx = Ndy. Where M is a function of x and N is the function of y. (2)
- Solve y’ = 2xy, y(0) = 1 (1)
Answer:
1. Degree = 1
2. We have, \(\frac{d y}{d x}\) = 2xy ⇒ \(\frac{d y}{y}\) = 2xdx, which is of the form Mdx = Ndy.
3. Solution is ∫\(\frac{d y}{y}\) = 2∫xdx ⇒ log|y| = x2 + c
Given y(0) = 1 ⇒ log|1| = 0 + c ⇒ c = 0
⇒ log|y| = x2 ⇒ y = ex2.
Question 6.
Solve the following DE \(\frac{d y}{d x}=\frac{y^{2}-x^{2}}{2 x y}\).
Answer:
\(\frac{d y}{d x}=\frac{y^{2}-x^{2}}{2 x y}\), this is a Homogeneous DE.
Therefore, put y = vx and \(\frac{d y}{d x}\) = v + x\(\frac{d v}{d x}\) to convert it into variable separable form.
The DE becomes,
![]()
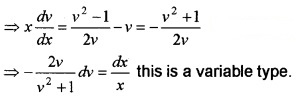
Therefore integrating we get,
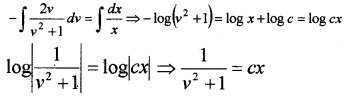
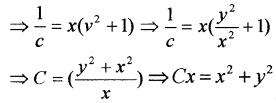
Question 7.
Solve the linear differential equation \(x \frac{d y}{d x}-y=(x-1) e^{x}\).
Answer:
Given, x\(\frac{d y}{d x}\) – y = (x – 1)ex, dividing both sides by x ,we get

Solution is
y × IF = ∫Q(IF)dx + c
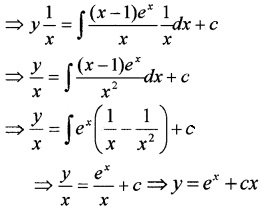
Question 8.
(i) Choose the correct answer from the bracket. The solution of the differential equation xdy + ydx = 0 represents (1)
(a) a rectangular hyperbola
(b) a parabola whose centre is origin
(c) a straight line whose centre is origin
(d) a circle whose centre is origin.
(ii) From the DE of the family of circles touching the x-axis at origin. (3)
Answer:
(i) (c) a straight line whose centre is origin.
(ii) Let (0, a) be the centre of the circle. Therefore the equation of the circle is
x2 + (y – a)2 = a2
⇒ x2 + y2 = 2ay
⇒ \(\frac{x^{2}+y^{2}}{y}\) = 2a ____(1)
Differentiating with respect to x,
Question 9.
Solve the DE x2\(\frac{d y}{d x}\) = x2 – 2y2 + xy.
Answer:
x2\(\frac{d y}{d x}\) = x2 – 2y2 + xy
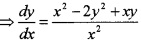
this is a Homogeneous DE.
Put y = vx and \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)
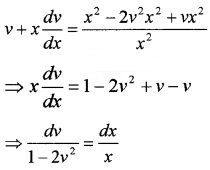
Integrating on both sides,
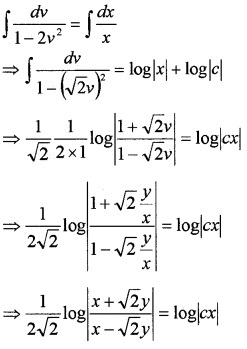
Question 10.
Choose the correct answer from the bracket
- The DE \(\frac{d y}{d x}+\frac{y}{x}\) = ex, x > 0 is of order …..[0,1,2,3] (1)
- The integrating factor \(\frac{d y}{d x}+\frac{y}{x}\) = ex, is……..[x, ex, -x, e-x] (1)
- Solve \(\frac{d y}{d x}+\frac{y}{x}\) = ex (2)
Answer:
1. Order = 1
2. \(\frac{d y}{d x}+\frac{y}{x}\) = ex is of the form \(\frac{d y}{d x}\) + Py = Q,
where P = \(\frac{1}{x}\), Q = ex
IF = e∫Pdx = e∫\(\frac{1}{x}\)dx = elogx = x
3. Solution is y.IF = ∫ex. IFdx
⇒ yx = ∫x.exdx ⇒ yx = x.ex – ∫exdx
⇒ yx = x.ex – ex + c ⇒ yx = ex(x – 1) + c.
Question 11.
Solve the DE \(\frac{d y}{d x}=\frac{x+y}{x-y}\).
Answer:
\(\frac{d y}{d x}=\frac{x+y}{x-y}\), this is a Homogeneous DE.
Put y = vx and \(\frac{d y}{d x}\) = v + x\(\frac{d v}{d x}\)
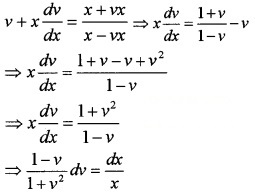
Integrating on both sides,
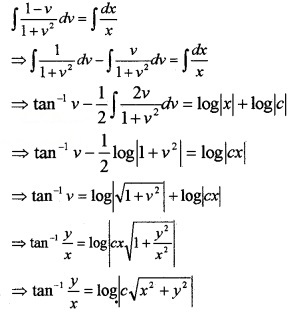
Plus Two Maths Differential Equations Six Mark Questions and Answers
Question 1.
Consider the DE \(\frac{d y}{d x}=\frac{y^{3}+3 x^{2} y}{x^{3}+3 x y^{2}}\)
- Identify the DE ? Give reason. (1)
- Explain the method of solving the DE. (1)
- Solve the DE. (4)
Answer:
1. Given DE is a Homogeneous DE. Since y3 + 3x2y and x3 + 3xy2 are Homogeneous functions of same degree (deg = 3).
2. By giving a substitution y = v x and \(\frac{d y}{d x}\) = v + x\(\frac{d y}{d x}\)
we can convert the DE into variable separable.
3. Now we have, \(\frac{d y}{d x}=\frac{y^{3}+3 x^{2} y}{x^{3}+3 x y^{2}}\)
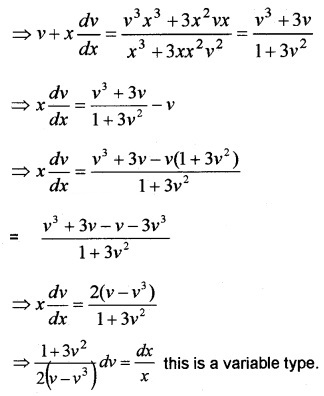
∴ Integrating we get,
\(\int \frac{1+3 v^{2}}{2 v\left(1-v^{2}\right)} d v=\int \frac{d x}{x}\)
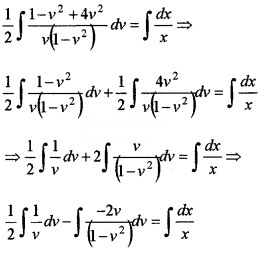
\(\frac{1}{2}\) log v – log(1 – v2) = log x + log c
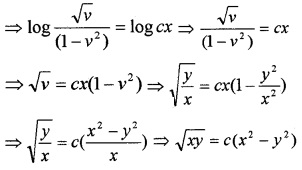
Question 2.
Consider the D.E \(\frac{d y}{d x}+\frac{y}{x}=x^{2}\)
- Find degree and order of DE . (1)
- Solve the D.E. (4)
- Find the particular solution when x = 1, y = 1. (1)
Answer:
1. Degree: 1, Order: 1.
2. The given D.E is first order linear DE of the form
\(\frac{d y}{d x}\) + Py = Q. Comparing we get, P = \(\frac{1}{x}\), Q = x2
∴ ∫Pdx = ∫\(\frac{1}{x}\)dx = logx
Integrating factor (I.F) = e∫Pdx = elogx = x
y.x = ∫x2.xdx + c = ∫x3 dx + c
⇒ y.x = \(\frac{x^{4}}{4}\) + c ___(1)
3. Given, y = 1 when x = 1, then (1)
⇒ 1 × 1 = \(\frac{1}{4}\) + c ⇒ c = \(\frac{3}{4}\)
Therefore particular solution is
y.x = \(\frac{x^{4}}{4}\) + \(\frac{3}{4}\) ⇒ 4xy = x3 + 3.
Question 3.
Consider the equation.\(\frac{d y}{d x}\) + y = sin x
- What is the order and degree of this equation? (1)
- Find the integrating factor. (2)
- Solve this equation. (3)
Answer:
1. Order = 1, Degree = 1
2. Given, \(\frac{d y}{d x}\) + y = sin x is of the form
\(\frac{d y}{d x}\) + Py = Q ⇒ P = 1, Q = sinx
Integrating factor = e∫Pdx = e∫1dx = ex
3. Therefore solution is
y.IF = ∫Q.IFdx + c ⇒ yex = ∫ex sinxdx + c ____(1)
∫sinx.exdx = ex sinx – ∫cosx.exdx
= ex sin x – cosx.ex – ∫sinx.ex dx
⇒ 2∫ex sin xdx = ex(sin x – cos x)
⇒ ∫ex sinxdx = \(\frac{e^{x}}{2}\)(sinx – cosx)
(1) ⇒ yex = \(\frac{e^{x}}{2}\)(sinx – cosx) + c.
Question 4.
Considerthe D.E (x2 – 1)\(\frac{d y}{d x}\) + 2(x + 2)y = 2(x + 1)
- Find \(\frac{d y}{d x}\), degree and order of the above differential equation. (1)
- Find the integrating factor of the above differential equation. (2)
- Solve the differential equation. (3)
Answer:
1. Given, (x2 – 1)\(\frac{d y}{d x}\) + 2(x + 2)y = 2(x + 1)
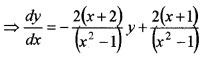
Here, Degree = 1, Order = 1.
2. The given DE is of the form \(\frac{d y}{d x}\) + Py = Q
Where,
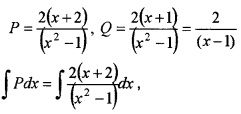
Splitting it into partial fractions we get,
![]()
Put x = 1, ⇒ 6 = 2B ⇒ B = 3,
put x = -1, ⇒ 2 = -2A ⇒ A = -1

3. Solution is y × IF = ∫Q × IFdx + c
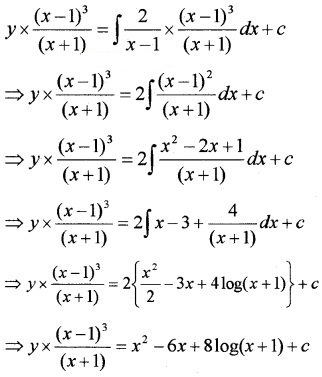
Question 5.
(i) The degree of the differential Equation \(\frac{d^{2} y}{d x^{2}}+\cos \left(\frac{d y}{d x}\right)=0\) is
(a) 2
(b) 1
(c) 0
(d) Not defined
(ii) Solve \(\frac{d y}{d x}\) + 2y tanx = sinx; y = 0, x = \(\frac{\pi}{3}\) (5)
Answer:
(i) (d) Not defined.
(ii) \(\frac{d y}{d x}\) + 2y tanx = sinx
Then, P = 2tanx, Q = sinx
IF = e∫Pdx = e∫2tanxdx = e2log sec x = sec2 x Solution is; y × IF = ∫Q(IF)dx + c
⇒ ysec2 x = ∫sinx sec2 xdx + c
⇒ ysec2 x = ∫tanx secx dx + c
⇒ ysec2x = secx + c
Here; y = 0, x = \(\frac{\pi}{3}\)
⇒ 0 × sec2 \(\frac{\pi}{3}\) = sec\(\frac{\pi}{3}\) + c ⇒ c = -2
⇒ ysec2 x = secx – 2.
Question 6.
(i) The order of the differential equation \(x^{4} \frac{d^{2} y}{d x^{2}}=1+\left(\frac{d y}{d x}\right)^{3}\) is
(a) 1
(b) 3
(c) 4
(d) 2
(ii) Find the particular solution of the (1 + x2) \(\frac{d y}{d x}\) + 2 xy = \(\frac{1}{1+x^{2}}\); y = 0, when x = 1 (5)
Answer:
(i) (d) 2
(ii) (1 + x2) \(\frac{d y}{d x}\) + 2 xy = \(\frac{1}{1+x^{2}}\); y = 0, when x = 1
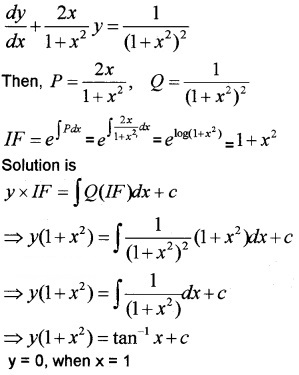
⇒ 0(1 + 12) = tan-11 + c ⇒ c = \(-\frac{\pi}{4}\)
⇒ y(1 + x2) = an-1x – \(\frac{\pi}{4}\).
We hope the given Plus Two Maths Chapter Wise Questions and Answers Chapter 9 Differential Equations will help you. If you have any query regarding Plus Two Maths Chapter Wise Questions and Answers Chapter 9 Differential Equations, drop a comment below and we will get back to you at the earliest.
