Plus Two Maths Chapter Wise Questions and Answers Chapter 5 Continuity and Differentiability are part of Plus Two Maths Chapter Wise Questions and Answers. Here we have given Plus Two Maths Chapter Wise Questions and Answers Chapter 5 Continuity and Differentiability.
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus Two |
| Subject | Maths Chapter Wise Questions |
| Chapter | Chapter 5 |
| Chapter Name | Continuity and Differentiability |
| Number of Questions Solved | 56 |
| Category | Plus Two Kerala |
Kerala Plus Two Maths Chapter Wise Questions and Answers Chapter 5 Continuity and Differentiability
Plus Two Maths Continuity and Differentiability Three Mark Questions and Answers
Question 1.
Consider the function g(x) = \(\frac{|x-2|}{x-2}\)
- Find the domain and range of the function g(x). (2)
- Check whether the g(x) is continuous at x = 2. (1)
Answer:
1. The function is not defined at points where the denominator is zero.
i.e., x – 2 = 0 ⇒ x = 2.
∴ domain is R – {2}.
g(x) = \(\frac{|x-2|}{x-2}\) = \(\left\{\begin{array}{c}{\frac{x-2}{x-2}, \quad x-2>0} \\{\frac{-(x-2)}{x-2}, \quad x-2<0}\end{array}=\left\{\begin{array}{ll}{1,} & {x>2} \\{-1,} & {x<2}\end{array}\right.\right.\)
∴ range is {-1, 1}
2. The function g(x) is not defined at x = 2. Therefore discontinuous.
Question 2.
(i) If f(x) = x+|x| + 1, then which of the follow represents f (x) (1)
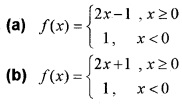
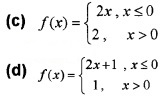
(ii) Test whether f (x) is continuous at x=0. Explain. (2)
Answer:
(i) (b) Since, f(x) = \(\left\{\begin{array}{c}{x+x+1, x \geq 0} \\{x-x+1, \quad x<0}
\end{array}=\left\{\begin{array}{c}{2 x+1, x \geq 0} \\{1, x<0}\end{array}\right.\right.\)
(ii) We have ,f (0) = 1,
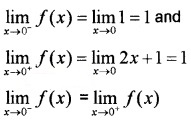
Continuous at x = 0.
Question 3.
Consider the function f(x) = \(\left\{\begin{array}{ll}{\frac{\sin x}{x}} & {, x<0} \\{x+1} & {, x \geq 0}\end{array}\right.\)
- Find \(\lim _{x \rightarrow 0} f(x)\) (2)
- Is f (x) continuous at x= 0? (1)
Answer:
1. To find \(\lim _{x \rightarrow 0} f(x)\) we have to find f(0– )and f(0+)
f(0–) = \(\lim _{x \rightarrow 0} \frac{\sin x}{x}=1\),
f(0+) = \(\lim _{x \rightarrow 0}\) + 1 = 0 + 1 = 1
f(0–) = f(0+) = 1 .Therefore \(\lim _{x \rightarrow 0} f(x)\) = 1
2. Here, f (0) = 0 + 1 = 1 = f(0–) = f(0+) = 1
Therefore continuous at x = 0.
Question 4.
Consider the figure and answer the following questions.
(i) Identify the graphed function. (1)
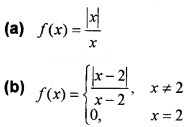
(ii) Discuss the continuity of the above function at x = 2. (2)
Answer:
(i) (b) f(x) = \(\left\{\begin{array}{ll}{\frac{|x-2|}{x-2},} & {x \neq 2} \\{0,} & {x=2}\end{array}\right.\)
(ii) From the figure we can see that
f(2–) = 1, f(2+) = -1 and f(2) = 0
Therefore, f(2–) = 1 ≠ f(2+) = -1 ≠ f(2) = 0. Discontinuous.
Question 5.
Consider f(x) = \(\left\{\begin{array}{ll}{2 x} & {\text { if } x<2} \\{2} & {\text { if } x=2} \\ {x^{2}} & {\text { if } x>2}\end{array}\right.\)
(a) Find \(\lim _{x \rightarrow 2^{-}} f(x)\) and \(\lim _{x \rightarrow 2^{+}} f(x)\) (2)
(b) f(x) is continuous. If not so, how can you make it continuous. (1)
Answer:
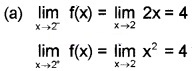
![]()
Therefore f(x) is not continuous at x = 2.
If f(2) = 4, then f(x) becomes continuous.
Question 6.
If y = log10x + logx10 + logxx + log1010. Find \(.
Answer:
y = loge x log10e + loge10 logxe + 1 + 1
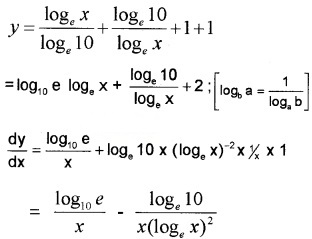
Question 7.
Examine the continuity of the function
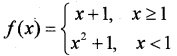
Answer:
In both the intervals x = 1 and x < 1 the function f(x) is a polynomial so continuous. So we have to check the continuity at x = 1.
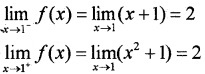
f(1) = 2
Since
![]()
f(x) is continuous at x = 1.
Question 8.
Find [latex]\frac{d y}{d x}\) of the following (3 score each)
- 2x + 3y = sinx
- xy + y2 = tanx + y
- x3 + x2y + xy2 + y3 = 81
- sin2x + cos2y = 1
- \(\sqrt{x}\) + \(\sqrt{y}\) = 1
- x2 + xy + y2 = 7
- x2(x – y) = y2(x + y)
- xy2 + x2y = 2
- sin y = xcos (a + y)
Answer:
1. Given; 2x + 3y = sinx
Differentiating with respect to x;
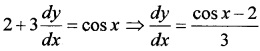
2. Given; xy + y2 = tanx + y
Differentiating with respect to x;
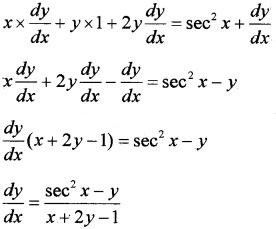
3. Given; x3 + x2y + xy2 + y3 = 81
Differentiating with respect to x;
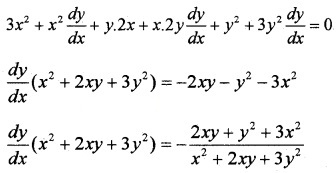
4. Given; sin2x + cos2y = 1
Differentiating with respect to x;
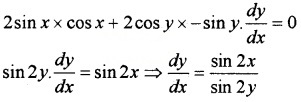
5. \(\sqrt{x}\) + \(\sqrt{y}\) = 1
Differentiating with respect to x;
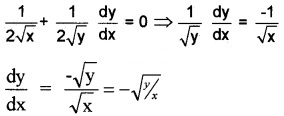
6. x2 + xy + y2 = 7
Differentiating with respect to x;
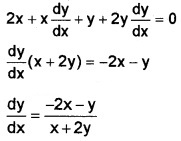
7. x2(x – y) = y2(x + y)
Differentiating with respect to x;
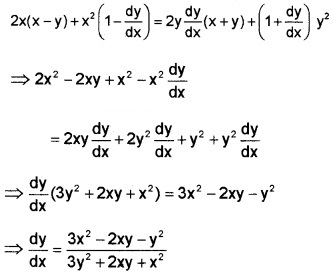
8. xy2 + x2y = 2
Differentiating with respect to x;
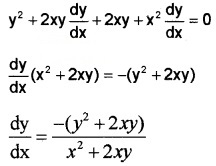
9. sin y = xcos (a + y)
⇒ x = \(\frac{\sin y}{\cos (a+y)}\)
Diff. with respect to y.
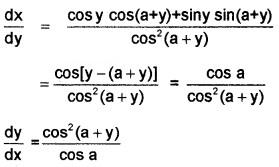
Question 9.
Find \(\frac{d y}{d x}\) of the following (3 score each)
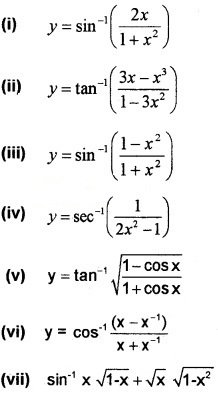
(viii) x = a(t – sint), y = a(1 – cost)
(ix) y = et cost, x = et sint.
Answer:
(i) We know; y = sin-1\(\left(\frac{2 x}{1+x^{2}}\right)\)
⇒ y = = 2 tan-1(x)
Differentiating with respect to x;
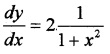
(ii) We know; y = tan-1\(\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)\)
Put x = tanθ ⇒ θ = tan-1x
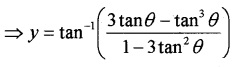
⇒ y = tan-1(tan3θ)
⇒ y = 3 tan-1(x)
Differentiating with respect to x;
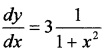
(iii) We know; y = sin-1\(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)
Put x = tanθ ⇒ θ = tan-1x
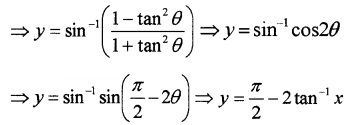
(iv) We know; y = sec-1 = \(\left(\frac{1}{2 x^{2}-1}\right)\)
Put x = cosθ ⇒ θ = cos-1x
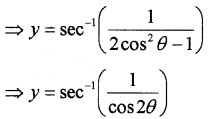
⇒ y = sec-1 sec2θ = 2θ
⇒ y = 2cos-1(x)
Differentiating with respect to x;
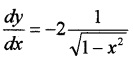
(v) ∴ y = tan-1\(\sqrt{\tan ^{2} x / 2}\) = tan-1 tanx/2 = x/2
\(\frac{d y}{d x}=\frac{1}{2}\).
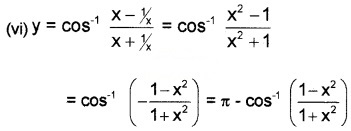
= π – 2tan-1x
\(\frac{d y}{d x}=\frac{-2}{1+x^{2}}\).
(vii) Let x = sinθ and \(\sqrt{x}\) = sinφ
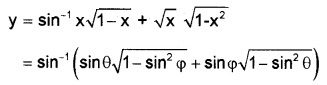
= sin-1 (sinθcosφ + cosφsinφ)
= sin-1 (sin(θ + φ)) = θ + φ
= sin-1x + sin-1\(\sqrt{x}\)
\(\frac{d y}{d x}=\frac{1}{\sqrt{1-x^{2}}}+\frac{1}{\sqrt{1-x}} \times \frac{1}{2 \sqrt{x}}\).
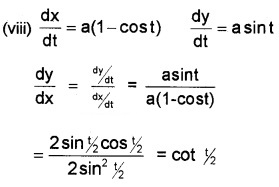
(ix) y = etcost ⇒ \(\frac{d y}{d t}\) = – et sin t + et
x = et sint ⇒ \(\frac{d x}{d t}\) = et cos t + et sin t
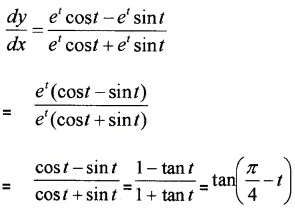
Question 10.
If y = log\(\left(\frac{1}{x}\right)\), Show that \(\frac{d y}{d x}\) + ey = 0.
Answer:
Given, y = log\(\left(\frac{1}{x}\right)\) ? \(\left(\frac{1}{x}\right)\) = ey …….(1)
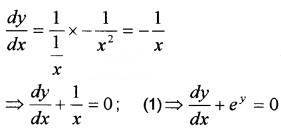
Question 11.
If ey (x+1) = 1. Show that
- \(\frac{d y}{d x}\) = -ey (2)
- \(\frac{d^{2} y}{d x^{2}}=\left(\frac{d y}{d x}\right)^{2}\) (1)
Answer:
1. ey (x+1) = 1
Differentiating ey +ey(x +1) \(\frac{d y}{d x}\) = 0
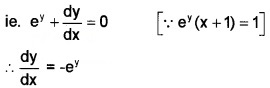
2.
![]()
Question 12.
(i) Evaluate \(\lim _{x \rightarrow 0} \frac{k \cos x}{\pi-2 x}\) (2)
(Hint: Put π – 2x = y , where Iris a constant)
(ii) Find the value of k if f (x) is a continuous function given by (1)
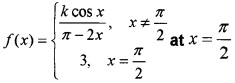
Answer:
(i) \(\lim _{x \rightarrow \pi / 2} \frac{k \cos x}{\pi-2 x}=k \lim _{x \rightarrow \pi / 2} \frac{\cos x}{\pi-2 x}\),
Put π – 2x = y when Put x → π/2, y → 0
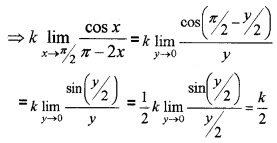
(ii) Since f (x) is continuous
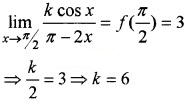
Question 13.
If f(x) \(f(x)=\left\{\begin{array}{cc}{x-[x]} & {, x<.2} \\{0} & {; x=2} \\{3 x-5} & {, x>2}
\end{array}\right.\)
- Find \(\lim _{x \rightarrow 2} f(x)\) (2)
- Is f(x) continuous at x = 2? (1)
Answer:
1. To find \(\lim _{x \rightarrow 2} f(x)\)
we have to find f(2–) and f(2+)
f(2–) = \(\lim _{x \rightarrow 2} x-[x]\) = 2 -1 = 1,
f(2+) = \(\lim _{x \rightarrow 2}\) 3x – 5 = 6 -5 = 1
f(2–) = f(2+) = 1.
Therefore \(\lim _{x \rightarrow 2}\) f(x) = 1
2. Here, f(2) = 0 ≠ f(2–) = f(2+) = 1.
Therefore discontinuity at x = 2.
Plus Two Maths Continuity and Differentiability Four Mark Questions and Answers
Question 1.
If x = 2cosθ; y = 3sinθ
- Find \(\frac{d y}{d x}\).
- Find \(\frac{d^{2} y}{d x^{2}}\)
Answer:
1. x = 2cosθ ⇒ \(\frac{d x}{d θ}\) = -2sinθ
y = 3sinθ ⇒ \(\frac{d x}{d θ}\) = 3cosθ
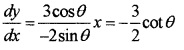
2.
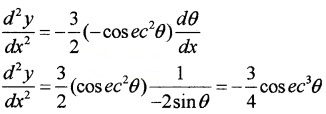
Question 2.
If y = (tan-1 x)2, show that (x2 +1)2 y2 + 2x(x2 +1) y1 = 2.
Answer:
y = (tan-1 x)2
⇒ y1 = 2(tan-1 x) \(\frac{1}{1+x^{2}}\)
⇒ (1 + x2)y1 = 2(tan-1 x)
⇒ (1 + x2)y2 + y12x = 2 \(\frac{1}{1+x^{2}}\)
⇒ (1 + x2)2 y2 + x(1 + x2)y1 = 2.
Question 3.
Find \(\frac{d y}{d x}\) if y = sin-1 \(\left(\frac{1-x^{2}}{1+x^{2}}\right)\), 0 < x < 1.
Answer:
Put x = tanθ
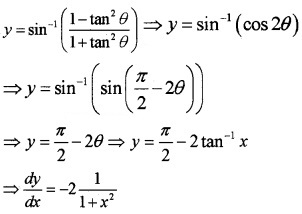
Question 4.
Let f(x) = \(\left\{\begin{array}{ll}{\cos x,} & {0 \leq x \leq c} \\{\sin x,} & {c<x \leq \pi}\end{array}\right.\)
- Find the value of c if / is continuous on [0, π].
- Show that is f not differentiable at the point c.
Answer:
1. Since f is continuous on [0, π], we have;
\(\lim _{x \rightarrow c^{+}}\) f(x) = \(\lim _{x \rightarrow c^{-}}\) f(x) = f(c)
⇒ \(\lim _{x \rightarrow c^{+}}\) sinx = \(\lim _{x \rightarrow c^{-}}\) cosx = cosc
⇒ sinc = cosc ⇒ c = \(\frac{π}{4}\).
2. \(f^{\prime}(x)=\left\{\begin{array}{ll}{-\sin x,} & {0 \leq x \leq c} \\{\cos x,} & {c<x \leq \pi}\end{array}\right. \)
Left derivative at \(\frac{\pi}{4}\) = – sin \(\frac{\pi}{4}\) = –\(\frac{1}{\sqrt{2}}\)
Right derivative at \(\frac{\pi}{4}\) = cos \(\frac{\pi}{4}\) = \(\frac{1}{\sqrt{2}}\)
Left derivative at \(\frac{\pi}{4}\) ≠ Right derivative at \(\frac{\pi}{4}\)
Therefore is not differentiable at the point c.
Question 5.
- Find \(\frac{d y}{d x}\) if x = 2sinθ; y = 3cosθ
- Which among the following functions is differentiable on R?
(a) |sinx|
(b) |cosx|
(c) cos|x|
(d) sin|x|
Answer:
1. \(\frac{d x}{d θ}\) = 2cosθ; \(\frac{d y}{d θ}\) = -3 sinθ ⇒ \(\frac{d y}{d x}\) = \(-\frac{3}{2}\)tanθ
2. (c) cos|x|
(Since cos x is an even function, it treats x and -x in the same way).
Question 6.
(i) Examine whether the function defined by \(f(x)=\left\{\begin{array}{ll}{x+5,} & {x \leq 1} \\{x-5,} & {x>1}\end{array}\right.\) is continuous or not. (2)
(ii) If x = sin-1t, y = cos-1t, a > 0, show that \(\frac{d y}{d x}=-\frac{y}{x}\)
Answer:
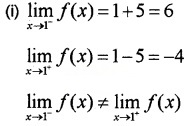
f(x) is not continuous.
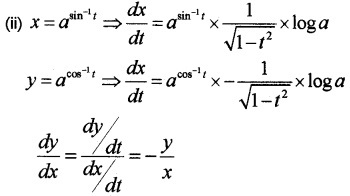
Question 7.
(i) If \(f(x)=\left\{\begin{array}{ll}{1-x,} & {0 \leq x \leq 1} \\{1+x,} & {1<x \leq 2}\end{array}\right.\) then which of the following is not true (1)
(a) f is continuous in ( 0, 1 )
(b) f is continuous in (1, 2 )
(c) f is continuous in [ 0, 2 ]
(d) f is continuous in [ 0,1 ]
if \(\left\{\begin{array}{cc}{1,} & {x \leq 3} \\{a x+b} & {, \quad 3<x<5} \\{7,} & {5 \leq x}\end{array}\right.\)
(ii) Find f(3+) and f(5–) (1)
(iii) Hence find the value of ‘a’ and ‘b’ so that f(x) is continuous. (2)
Answer:
(i) (c) Since f is not continuous at x = 1.
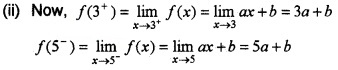
(iii) Since f (x) is continuous, it is continuous at x = 3 and x = 5
∴ f(3+) = f(3) ⇒ 3a + b = 1 ____(1)
and f(5–) = f(5) ⇒ 5a + b = 7 ____(2)
(2) – (1) ⇒ 2a = 6, a = 3
(1) ⇒ b = 1 – 3 a ⇒ b = -8
∴ a = 3, b = – 8.
Question 8.
Consider f(x) = \(\left\{\begin{array}{ll}{2 x+3,} & {x \leq 2} \\{x+2 k,} & {x>2}\end{array}\right.\)
- Find f(2) (1)
- Evaluate \(\lim _{x \rightarrow 2^{+}}\)f(x) (1)
- Find the value of k, if is continuous at x = 2. (2)
Answer:
1. f(2) = 2(2) + 3 = 7
2. Here, f(x) = x + 2k for x > 2.
\(\lim _{x \rightarrow 2^{+}}\)f(x) = \(\lim _{x \rightarrow 2}\)(x + 2k) = 2 + 2k.
3. Since f (x) is continuous at x = 2
We have, f(2) = \(\lim _{x \rightarrow 2^{+}}\)f(x)
⇒ 7 = 2 + 2k ⇒ k = \(\frac{5}{2}\)
Question 9.
Find \(\frac{d y}{d x}\) of the following (4 score each)
- y = (logx)cosx
- x = 2at2, y = at4
- x = a(cosθ + θsinθ), y = a(sinθ – θcosθ)
- y=xx
- y =(x log x)log(logx)
- y = \(\sqrt{\sin x \sqrt{\sin x+\sqrt{\sin x+\ldots .}}}\)
- yx = xsiny
- y =(log x)x + xlogx
- y = (sinx)x + sin-1 \(\sqrt{x}\)
Answer:
1. Given; y = (logx)cosx, taking log on both sides;
log y = cosxlog(logx),
Differentiating with respect to x;
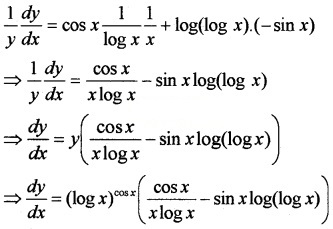
2. Given; x = 2at2 ⇒ \(\frac{d x}{d t}\) = 4at
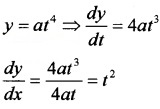
3. Given; x = a(cosθ + θsinθ)
\(\frac{d x}{d \theta}\) = a(-sinθ + θcosθ + sinθ) = aθcosθ
y = a(sinθ – θcosθ)
\(\frac{d x}{d \theta}\) = a(cosθ – θ(-sinθ) – cosθ) = aθ sinθ
\(\frac{d y}{d x}=\frac{a \theta \sin \theta}{a \theta \cos \theta}=\tan \theta\)
4. y= xx; Taking log on both sides;
log y = x log x
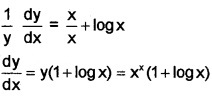
5. y = (x log x)log logx
Taking log on both sides;
log y = (log log x) [log (xlogx)]
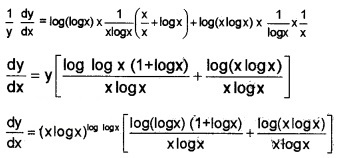
6. y = \(\sqrt{\sin x+y}\) ⇒ y2 = sinx + y
⇒ y2 – y = sinx
![]()
7. yx = xsin y;
Taking log on both sides;
xlogy = siny log x
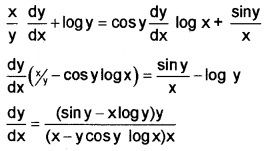
8. y = (log x)x + xlogx = u + v
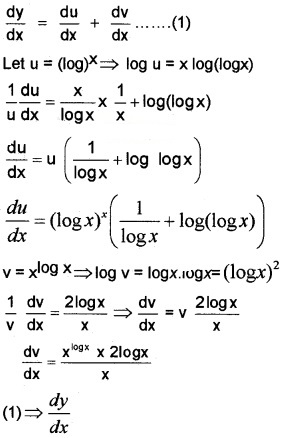

9. y = (sinx)x + sin-1\(\sqrt{x}\)
Let u = (sinx)x ⇒ log u = x log sinx
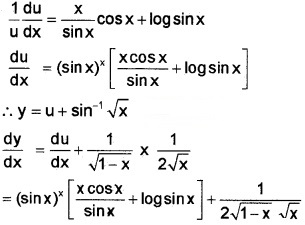
Question 10.
Find \(\frac{d^{2} y}{d x^{2}}\) of the following
- y = x2 + 3x + 2 (2)
- y = tan-1x (2)
Answer:
1. Given; y = x2 + 3x + 2
Differentiating with respect to x;
\(\frac{d y}{d x}\) = 2x + 3
Differentiating again with respect to x;
\(\frac{d^{2} y}{d x^{2}}\) = 2.
2. Given; y = tan-1x
Differentiating with respect to x; \(\frac{d y}{d x}\) = \(\frac{1}{1+x^{2}}\)
Differentiating again with respect to x;
\(\frac{d^{2} y}{d x^{2}}\) = \(-\frac{1}{\left(1+x^{2}\right)^{2}} \cdot 2 x\).
Question 11.
Match the following. (4)

Answer:

Question 12.
If x – sint and y = sinmt show that
(i) y = sin(m sin-1x) (1)
(ii) \(\frac{d y}{d x}\) (1)
(iii) (1 – x2) y2 – xy1 + m2y = 0 (2)
Answer:
(i) x = sint, y = sinmt
t = sin-1x ⇒ y = sin(msin-1x).
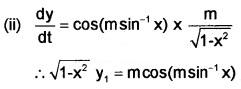
![]()
multiplying with \(\sqrt{1-x^{2}}\)
(1 – x2) y2 – xy1 = -m2y
(1 – x2) y2 – xy1 + m2y = 0.
Question 13.
Consider the function f(x) = x(x – 2), x ∈ [1, 3]. Verify mean value theorem for the function in[1, 3].
Answer:
f(x) = x(x – 2) = x2 – 2x ⇒ f'(x) = 2x – 2.
As f is a polynomial, it is continuous in the interval [1, 3] and differentiable in the interval (1, 3).
Therefore two conditions of MVT are satisfied and so there exists c ∈ (1,3)such that.
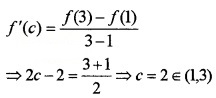
Hence MVT is verified.
Question 14.
Verify Lagranges’ Mean value theorem for the function f(x) = 2x2 – 10x + 29 in [2, 9]
Answer:
f(x) = 2x2 – 10x + 29; f'(x) = 4x – 10.
As f is a polynomial, it is continuous in the interval [2, 9] and differentiable in the interval (2, 9).
Therefore two conditions of MVT are satisfied and so there exists c ∈ (2, 9) such that.
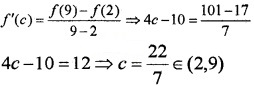
Hence MVT is verified.
Question 15.
Let f(x) = x(x – 1)(x – 2), x ∈ [0, 2]
- Find f(0) and f(2) (1)
- Find f'(x) (1)
- Find the values of x when f'(x) = 0 verify Rolle’s theorem. (2)
Answer:
1. f(0) = 0, f(2) = 2(2 – 1)(2 – 2) = 0
2. We have, f(x) = x3 – 3x2 + 2x
⇒ f'(x) = 3x2 – 6x + 2.
3. f'(x) = 3x2 – 6x + 2 = 0
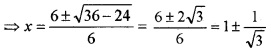
Clearly all the three conditions of Rolle’s theorem are satisfied and 1 ± \(\frac{1}{\sqrt{3}}\) ∈ (0, 2).
Question 16.
Verify Rolle’s Theorem for the function
f(x) = x2 + 2x – 8, x ∈ [-4, 2]
Answer:
f(x) = x2 + 2x – 8, f'(x) = 2x + 2.
As f is a polynomial, it is continuous in the interval [-4, 2] and differentiable in the interval (-4, 2).
f(-4) = 16 – 8 – 8 = 0
f(2) = 4 + 4 – 8 = 0
f'(c) = 0 ⇒ 2c + 2 = 0 ⇒ c = -1 ∈ (-4, 2) Hence Rolle’s Theorem is verified.
Question 17.
Examine that Rolle’s Theorem is applicable to the following function in the given intervals, justify your answer.
- f(x) = [x], x ∈ [5, 9]
- f(x) = x2 – 1, x ∈ [1, 2]
Answer:
1. The function f(x) = [x] is not differentiable and continuous at integral values. So in the given interval [5, 9] the function is neither differentiable nor continuous at x = 6, 7 ,8. Therefore Rolle’s Theorem is not applicable.
2. The function f(x) = x2 – 1 is a polynomial function so differentiable and continuous.
f(1) = 1 – 1 = 0, f(2) = 4 – 1 = 3
f(1) ≠ f(2) . Therefore Rolle’s Theorem is not applicable.
Question 18.
Examine the continuity of the function
\(f(x)=\left\{\begin{array}{cc}{|x|+3,} & {x \leq-3} \\{-2 x,} & {-3<x<3} \\{6 x+2,} & {x \geq 3}\end{array}\right.\)
Answer:
In the intervals x ≤ -3, f(x) is the sum of a constant function and modulus function so continuous. In the intervals -3 < x < 3 and x ≥ 3the function f(x) is a polynomial so continuous. Hence we have to check the continuity at x = -3, x = 3.
At x = -3
f(-3) = 6
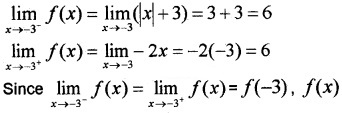
f(x) is continuous at x = -3.
At x = 3
f(3) = 6(3) + 2 = 20
![]()
Since \(\lim _{x \rightarrow 3^{-}}\)f(x) = f(3), f(x) is not continuous at x = 3.
Question 19.
Test continuity for the following functions.
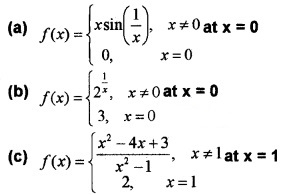
Answer:
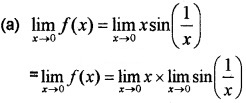
= 0 × a finite quantity between -1 and 1 = 0 Also f(0) = 0
Therefore f(x) is continuous at x = 0.
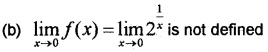
Therefore f(x) is discontinuous at x = 0
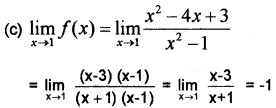
But f(1) = 2
∴ f(x) is discontinuous at x = 1.
Question 20.
If y = \(\frac{\sin ^{-1} x}{\sqrt{1-x^{2}}}\) prove that
(i) (1 – x2) y2 = (sin-1x)2 (1)
(ii) (1 – x2)y1 – xy = 1 (1)
(iii) (1 – x2) y2 – 3xy1 – y = 0 (2)
Answer:
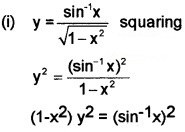
(ii) Differentiating
(1 – x2) 2y.y1 + y2x – 2x = \(\frac{2 \sin ^{-1} x}{\sqrt{1-x^{2}}}\)
(1 – x2)2yy1 – 2xy2 = 2y
(1 – x2) y1 – xy = 1.
(iii) Again differentiating
(1 – x2) y2 + y1 x – 2x – xy1 – y = 0
(1 – x2) y2 – 3xy1 – y = 0.
Question 21.
At what point on the curve y = x2, x ∈ [-2, 2] at which the tangent is parallel to x-axis?
Answer:
Y = x2, a continuous function on [-2, 2] and differentiable on [-2, 2] f(2) = 4 = f(-2). All conditions of Rolles theorem is satisfied. Given the tangent is parallel to x-axis.
f1 (x) = 2x
f1(c) = 2c
f1(c) = 0 ⇒ 2c = 0 ⇒ c = 0 ∈ [-2, 2]
where c = 0, y = 0
Therefore (0, 0) is the required point.
Question 22.
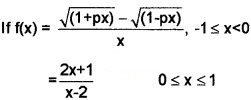
is continuous in the interval [-1 1].
(a) Find \(\lim _{x \rightarrow 0}\)f(x) (2)
(b) Find f(0). (1)
(c) Find P. (1)
Answer:

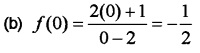
(c) Since f is continuous in [-1 1] it is continuous at 0.
Therefore P = \(-\frac{1}{2}\).
Question 23.
If ax2 + 2hxy + by2 = 1
- Find \(\frac{d y}{d x}\) (1)
- Find \(\frac{d^{2} y}{d x^{2}}\) (3)
Answer:
1. We have, ax2 + 2hxy + by2 = 1 ___(1)
Differentiating w.r.t.x, we get,
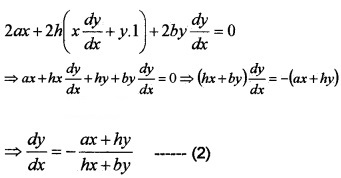
2. Differentiating (2) w.r.tx, we get,
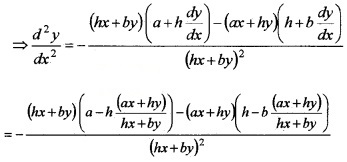
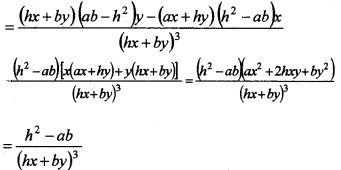
Question 24.
Consider the function y = xx \(\sqrt{x}\)
- Express the above function as logy = \(\left(x+\frac{1}{2}\right)\) logx (2)
- Find \(\frac{d y}{d x}\) (2)
Answer:
1. Given, y = xx \(\sqrt{x}\). Take log on both sides,
![]()
2. We have, logy = \(\left(x+\frac{1}{2}\right)\) logx
Differentiating w.r.t x, we get,
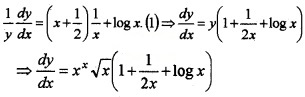
Plus Two Maths Continuity and Differentiability Six Mark Questions and Answers
Question 1.
- Verify mean value theorem for the function f(x) = (x – 2)2 in [1, 4].
- Find a point on the curve y = (x – 2)2 at which the tangent is parallel to the chord joining the points (1, 1) and (4, 2)
- Find a point on the above curve at which the tangent is parallel to the x-axis.
Answer:
1. f(x) = (x – 1)2, x ∈ [1, 4]
f(x) is continuous in [1, 4]
f'(x) = 2(x – 2) is differentiable in [1, 4]
Then there exists c ∈ [1, 4] so that
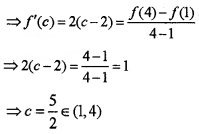
Hence Mean Value Theorem is verified.
2. c = \(\frac{5}{2}\) will be the x-coordinate to the point of contact of tangent and the curve, then y = (x – 2)2 ⇒ y = (\(\frac{5}{2}\) – 2)2 = \(\frac{1}{4}\)
Therefore the point is (\(\frac{5}{2}\), \(\frac{1}{4}\)).
3. The tangent parallel to x- axis will have
f'(c) = 0 ⇒ 2(c – 2) = 0 ⇒ c = 2
Then; x = 2 ⇒ y = (2 – 2)2 = 0
Therefore the point is (2, 0).
Question 2.
- Differentiate xsinx w.r.t.x (2)
- If x = at2, y = 2at, then find \(\frac{d y}{d x}\) (2)
- If y = sin-1(cosx) + cos-1(sinx), then find \(\frac{d y}{d x}\). (2)
Answer:
1. Let y = xsinx, take log on both sides,
log y = sinx logx differentiate w. r.t.x, we get
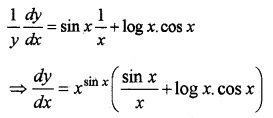
2.
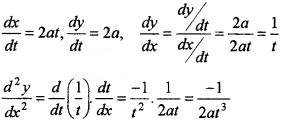
3. Given, y = sin-1(cosx) + cos-1(sinx)
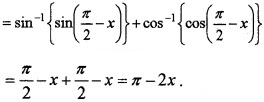
Differentiate w.r.t. x, we get \(\frac{d y}{d x}\) = -2.
Question 3.
- Differentiate \(\frac{x-1}{x-3}\) with respect to x.(2)
- Differentiate \(\sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}}\) with respect to x. (4)
Answer:
1. Let y = \(\frac{x-1}{x-3}\) Differentiate w.r.t. x, we get;
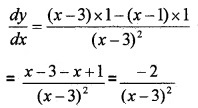
2. Given, y = \(\sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}}\)
Take log on both sides;
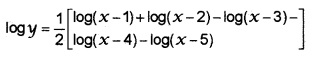
Differentiate w.r.t. x, we get;
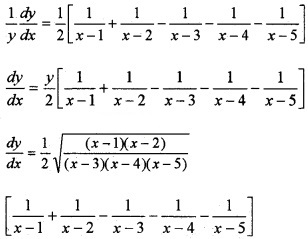
Question 4.
(i) Define |x|
(a) |x| = \(\sqrt{x^{2}}\)
(b) |x| = x
(c) |x| = -x
(d) |x| = x2
(ii) At which point \(\frac{d}{d x}\)|x| does not exist?
Find \(\frac{d}{d x}\) |x|. (2)
(iii) Find \(\frac{d}{d x}\)|x3 – 7x| . Also, find the point at which the derivative exists. (3)
Answer:
(i) (a) |x| = \(\sqrt{x^{2}}\).
(ii) At x = 0, \(\frac{d}{d x}\) |x| does not exist.
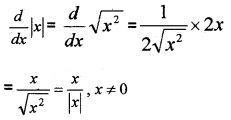
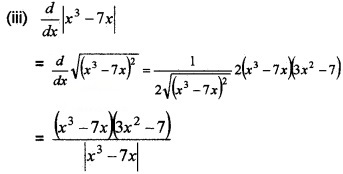
Does not exist at
x3 – 7x = 0 ⇒ x(x2 – 7) = 0
⇒ x = 0, x2 – 7 = 0 ⇒ x = ±\(\sqrt{7}\).
Question 5.
(i) Match the following (4)

(ii) If log (x2 + y2) = 2 tan-1\(\left(\frac{y}{x}\right)\), then, show that \(\frac{d y}{d x}=\frac{x+y}{x-y}\) (2)
Answer:
(i)
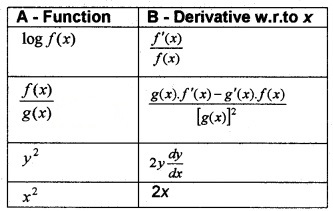
(ii) Given, log (x2 + y2) = 2 tan-1\(\left(\frac{y}{x}\right)\).
Differentiate w.r.to x, we get;
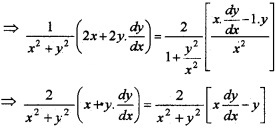
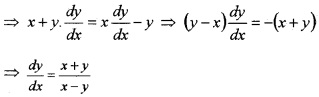
Question 6.
If x = a sec3θ and y = a tan3θ
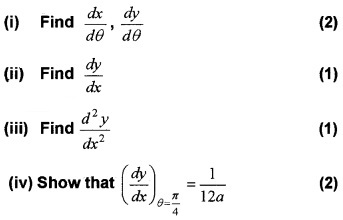
Answer:
(i) Given, x = a sec3θ
Differentiate w.r.to θ, we get;
\(\frac{d x}{d \theta}\) = 3a sec2θ. secθ. tanθ = 3a sec3 θ. tan θ
Given, y = a tan3θ .
Differentiating w.r.to θ, we get
\(\frac{d x}{d \theta}\) = 3a tan2 θ. sec2θ.
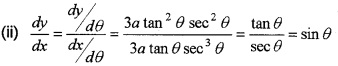
(iii) We have, \(\frac{d y}{d x}\) = sinθ
Differentiating w.r.to x, we get
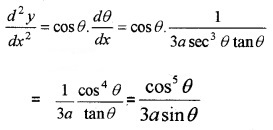
(iv) We have,
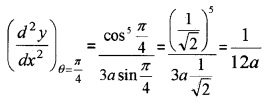
Question 7.
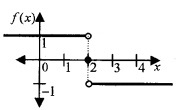
Consider the function \(f(x)=\left\{\begin{array}{cc}{1-x} & {, \quad x<0} \\{1} & {x=0} \\ {1+x} & {, \quad x>0}\end{array}\right.\)
(i) Compete the following table. (2)
![]()
(ii) Draw a rough sketch of f (x). (2)
(iii) What is your inference from the graph about Its continuity. Verify your answer using limits. (2)
Answer:

Since, f (- 2) = 1 – (- 2) = 3, f (-1) = 1 – (-1) = 2,
f(1) = 1 + (1) = 2, f (2) = 1 + (2) = 3.
(ii)
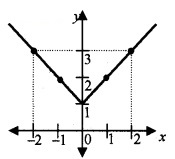
(iii) From the graph we can see that there is no break or jump at x = 0. Therefore continuous.
From the figure we can see that
f(0–) = 1 f(0+) = 1 and f(0) = 1
Hence, f(0–) = f(0+) = f(0) = 1.
Therefore continuous.
Question 8.
Consider the equation \(\sqrt{1-x^{2}}+\sqrt{1-y^{2}}=a(x-y)\)
(i) Simplify the above equation to sin-1x – sin-1y = 2cot-1 a by giving suitable substitution.
(ii) Prove that \(\frac{d y}{d x}=\sqrt{\frac{1-y^{2}}{1-x^{2}}}\)
Answer:
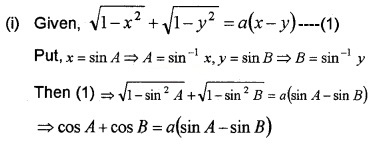
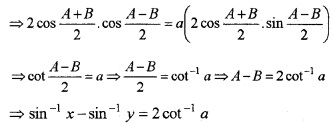
(ii) We have; sin-1 x – cos-1y = 2cot-1a.
Differentiating w.r.t x, we get,
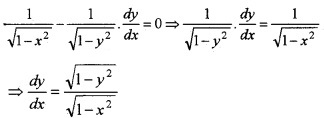
Question 9.
(i) Match the following. (4)
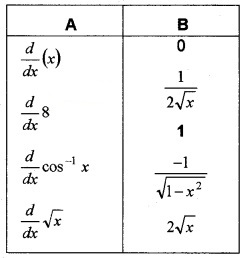
(ii) If y = ea cos-1x, then show that (1 – x2)y2 – xy1 – a2y = 0 (2)
Answer:
(i)
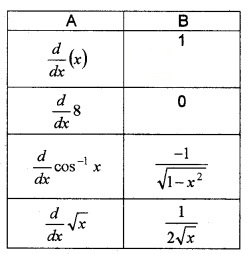
(ii) Given, y = ea cos-1x ____(1)
Differentiating w.r.to x,
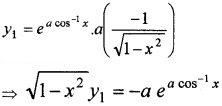
Again differentiating w. r.to x
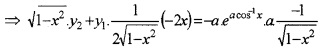
⇒ (1 – x2)y2 – xy1 = a2. ea cos-1x
⇒ (1 – x2)y2 – xy1 = a2y
⇒ (1 – x2)y2 – xy1 – a2y = 0.
Question 10.
(i) Match the following (3)
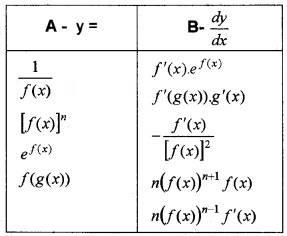
Differentiate the following
(ii) y =\(\frac{1}{5 x^{2}+3 x+7}\) (1)
(iii) y = 3cosec4(7x) (1)
(iv) y = e2log tan 5x (1)
Answer:
(i)

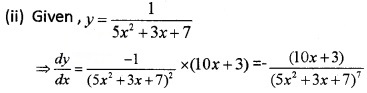
(iii) Given,
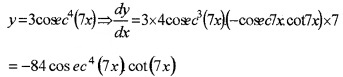
(iv) Given,
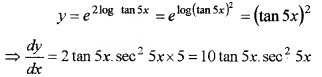
We hope the given Plus Two Maths Chapter Wise Questions and Answers Chapter 5 Continuity and Differentiability will help you. If you have any query regarding Plus Two Maths Chapter Wise Questions and Answers Chapter 5 Continuity and Differentiability, drop a comment below and we will get back to you at the earliest.
