Plus Two Maths Chapter Wise Previous Questions Chapter 9 Differential Equations

Plus Two Maths Chapter Wise Previous Questions Chapter 9 Differential Equations are part of Plus Two Maths Chapter Wise Previous Year Questions and Answers. Here we have given Plus Two Maths Chapter Wise Previous Chapter 9 Differential Equations.

Kerala Plus Two Maths Chapter Wise Previous Questions Chapter 9 Differential Equations

Plus Two Maths Differential Equations 3 Marks Important Questions

Question 1.
Form a differential equation of the family of circles having a centre on y-axis and radius 3 units. (May -2013)
Answer:
The equation of the circle passing through the point (O,k)and radius 3 is of the form

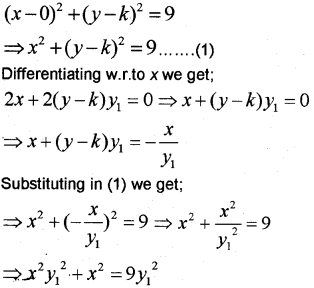
Question 2.
Consider the Differential equation
\(\frac{d^{2} y}{d x^{2}}+y=0\)
(i) Write the order and degree.
(ii) Verify that y = a cos x + b sin x where a,b ∈ R is a solution of the given DE. (March – 2014)
Answer:
(i) Order = 2; Degree = I
(ii) Given; y = acosx + bsin x
y₁ = – asin x + bcos x
y₂ = – acos x – bsin x
We have; y₂ = – (a cos x + b sin x)
⇒ y₂ = -y ⇒ y₂ + y = 0

Plus Two Maths Differential Equations 4 Marks Important Questions

Question 1.
If cosx\(\frac{d y}{d x}\) + y sin x = tan² x is a DE then
(i) Find its order and degree.
(ii) Find its general solution. (May -2010)
Answer:

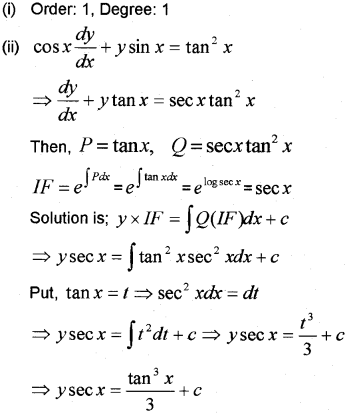
Question 2.
(i) Write the order and degree of the DE
\(\left[\frac{d y}{d x}\right]^{2}+\frac{d y}{d x}-\sin ^{2} y=0\)
(ii) Solve the \(\frac{d y}{d x}+2 y \tan x=\sin x\) (May-2011)
Answer:

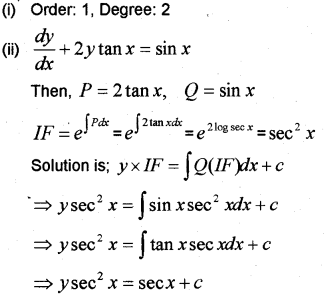
Question 3.
(i) The general solution of the DE \(\frac{d y}{d x}=e^{x-y} \text { is }\)
(a) e^y + e^x = c
(b) e^y e^x = c
(c) e^-y + e^-x = c
(d) e^-y – e^x = c
(ii) Solve the DE \(\frac{d y}{d x}=\frac{2 x y}{1+x^{2}}+x^{2}+2\) (March – 2013)
Answer:

Question 4.
(a) Consider the family of all circles having their centre at the point (1,2). Write the equation of the family. Write the corresponding differential equation.
(b) Write the integrating factor of the differential equation
\(\cos x \frac{d y}{d x}+y=\sin x, \quad 0 \leq x<\frac{\pi}{2}\) (March – 2015)
Answer:
(a) The equation of the circle ¡s

Question 5.
(a) Write the order and degree of the differential equations.
\(x y\left(\frac{d^{2} y}{d x^{2}}\right)^{2}+x\left(\frac{d y}{d x}\right)^{3}-y \frac{d y}{d x}=0\)

(b) Find the general solution of the differential equation ylog ydx – xdy = 0
(c) Find the integrating factor of the differential equation \(x \frac{d y}{d x}-y=2 x^{2}\) (May -2015)
Answer:

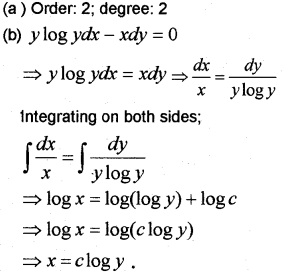
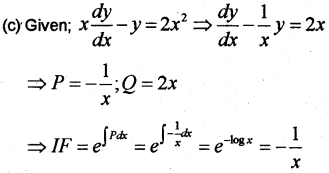
Question 6.
(a) y = a cosx +b sin x is the solution of the differential equation

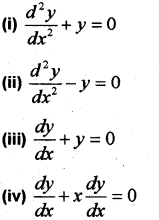
(b) Find the solution of the differential equation \(x \frac{d y}{d x}+2 y=x^{2}, \quad(x \neq 0)\) given that y = 0 when x=1. (March – 2016)
Answer:

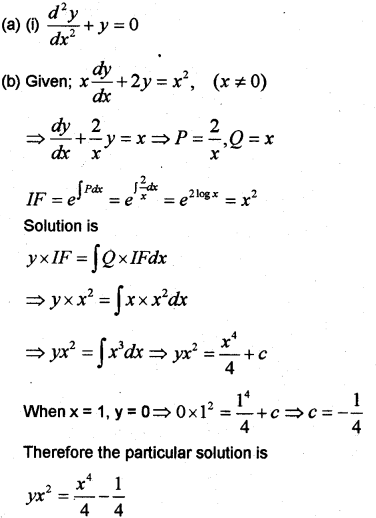
Plus Two Maths Differential Equations 6 Marks Important Questions

Question 1.
(i) Form the DE corresponding to the Function y = ae^x + be^2x
(ii) State the order and degree of the above DE.
(iii) Solve \(x \frac{d y}{d x}=x+y\) (March – 2009)
Answer:

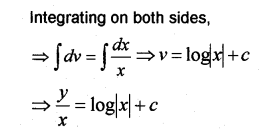
Question 2.
(i) Form the DE corresponding to the function Xy = C²
(ii) Consider the DE (x² + y² ) dx = 2xydy
(a) Write the DE in the ton \(\frac{d y}{d x}=g\left[\frac{y}{x}\right]\)
(b) Solve the DE completely (May -2009, May -2013)
Answer:

Question 3.
(i) Equation of a circle touching the y-axis at origin is x² + y² – 2ax = 0. Find the DE of all such circles.
(ii) SolvetheDE \(\left(1+x^{2}\right) \frac{d y}{d x}+y=\tan ^{-1} x\) (March – 2010)
Answer:

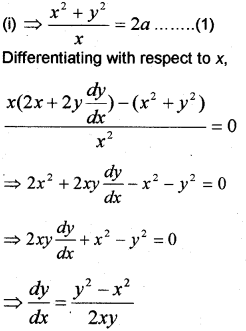
Question 4.
(i) Solution of the DE y^‘ – y = 0 is y = ………….
(ii) Solve the DE \(\Rightarrow \frac{d y}{d x}+y \sec x=\tan x\)
(iii) Form the DE of the family of ellipse having foci on the x-axis and centre at the origin. (March-2011)
Answer:

Question 5.
Consider the DE \(x d y-y d x=\sqrt{x^{2}+y^{2}} d x\)
(i) Express it in the form \(\frac{d y}{d x}\) = F(x, y)
(ii) Find the general solution. (March -2012; Edumate -2017)
Answer:

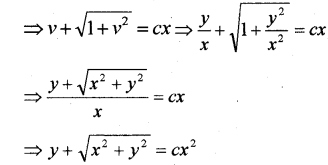
Question 6.
(i) Prove that the DE is (3xy + y²) dx + (x² + xy) dy = 0 a homogeneous DE of degree 0.
(ii) Solve the DE (3xy + y²) dx + (x² + xy) dy = 0 (May —2012, Edumate -2017)
Answer:

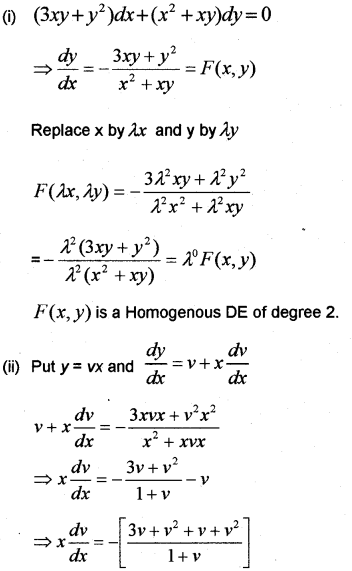
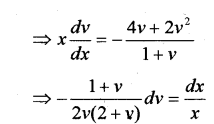
Question 7.
Consider the differential equation \(\frac{d y}{d x}-3 \cot x y=\sin 2 x\)
(a) Find its integrating factors.
(b) Fînd its solution, given that y = 2 When x = \(\frac{\pi}{2}\). (May-2014)
Answer:

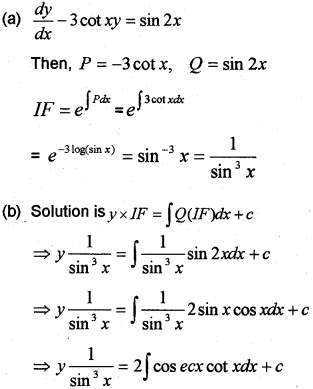
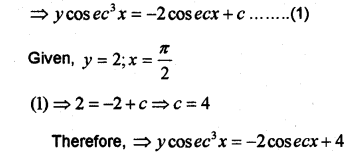
We hope the Plus Two Maths Chapter Wise Previous Questions Chapter 9 Differential Equations help you. If you have any query regarding Kerala Plus Two Maths Chapter Wise Previous Questions Chapter 9 Differential Equations, drop a comment below and we will get back to you at the earliest.