Plus Two Maths Chapter Wise Previous Questions Chapter 7 Integrals

Plus Two Maths Chapter Wise Previous Questions Chapter 7 Integrals are part of Plus Two Maths Chapter Wise Previous Year Questions and Answers. Here we have given Plus Two Maths Chapter Wise Previous Chapter 7 Integrals.

Kerala Plus Two Maths Chapter Wise Previous Questions Chapter 7 Integrals

Plus Two Maths Application of Derivatives 3 Marks Important Questions

Question 1.
Find the following integrals. (May -2011)
\(\begin{array}{l}
\text { (i) } \int x^{2} e^{2 x} d x \\
\text { (ii) } \int e^{x} \sin x d x
\end{array}\)
Answer:

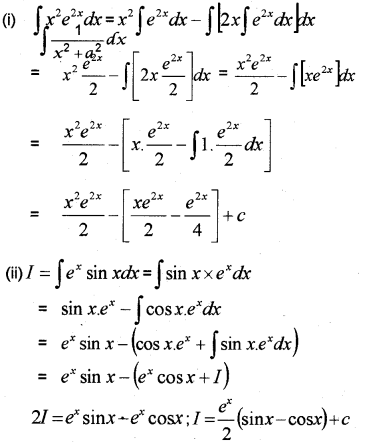
Question 2.
(i) \(\int e^{x} \sec x(1+\tan x) d x=\ldots \ldots\)
(a) ex cosx + c (b) ex sec x + c
(C) ex tanx + c (d) ex sin x + c
(ii) Find \(\int \sin 2 x \cos 3 x d x\) (March – 2014)
Answer:

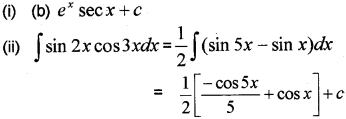
Question 3.
Find the following integrals.
(i) \(\begin{array}{l}
\text { (i) } \int \frac{1}{(x+1)(x+2)} d x \\
\text { (ii) } \int \frac{2 x-1}{(x-1)(x+2)^{2}} d x
\end{array}\) (March – 2014)
Answer:

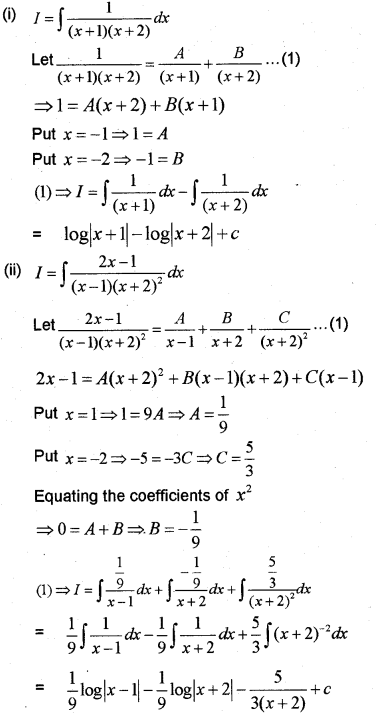
Plus Two Maths Application of Derivatives 4 Marks Important Questions

Question 1.
Consider the integral \(I=\int_{0}^{\pi} \frac{x \sin x}{1+\cos ^{2} x} d x\)
(i) Express \(I=\frac{\pi}{2} \int_{0}^{\pi} \frac{\sin x}{1+\cos ^{2} x} d x\)
(ii) Show that \(I=\frac{\pi^{2}}{4}\) (March – 2012)
Answer:

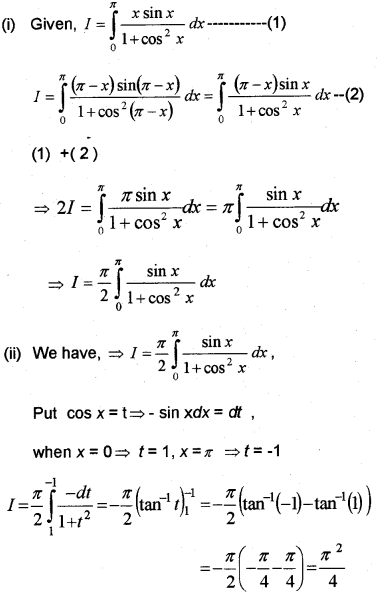
Question 2.
(i) Evaluate: \(\int_{2}^{3} \frac{x}{x^{2}+1} d x\)
(ii) Evaluate: \(\int_{0}^{\pi} \frac{x}{1+\sin x} d x\) (March – 2014)
Answer:

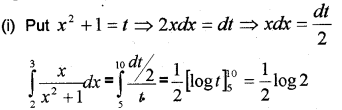
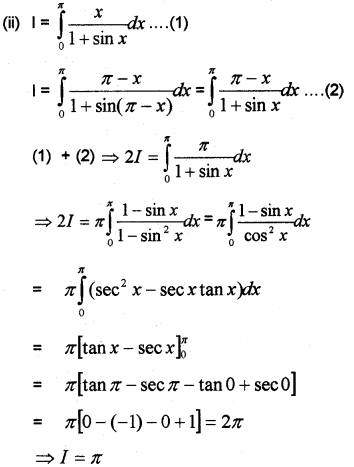
Question 3.
(a) What is the value of \(\int_{0}^{1} x(1-x)^{9} d x\) If the
\(\begin{array}{llll}
\text { (i) } \frac{1}{10} & \text { (ii) } \frac{1}{11} & \text { (iii) } \frac{1}{90} & \text { (iv) } \frac{1}{110}
\end{array}\)
(b) Find \(\int_{0}^{1}(2 x+3) d x\) of a sum. (March – 2015)
Answer:

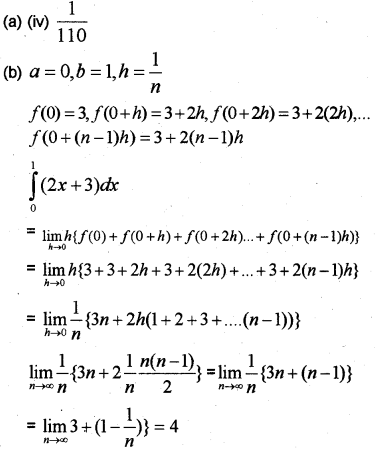
Question 4.
Evaluate \(\int_{0}^{x} \log (1+\cos x) d x\)
Answer:

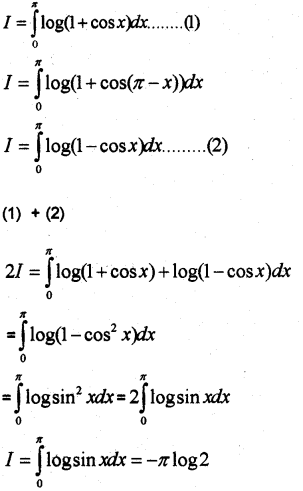
Question 5.
Find \(\int_{0}^{5}(x+1) d x \text { as limit of a sum. }\)
Answer:

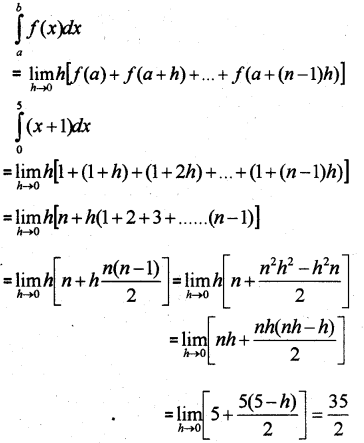
Question 6.
Evaluate \(\int_{0}^{4} x^{2} d x\) as the limit of a sum. (March – 2017)
Answer:

Plus Two Maths Application of Derivatives 6 Marks Important Questions

Question 1.
(i) Fill in the blanks; \(\int \frac{1}{x} d x=\)_____
(ii) Evaluate \(\int \frac{5 x+1}{x^{2}-2 x-35} d x\)
(iii) Integrate with respect to x. \(\sqrt{x^{2}+4 x+8}\) (March – 2010)
Answer:

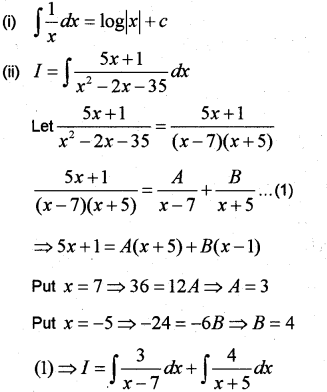
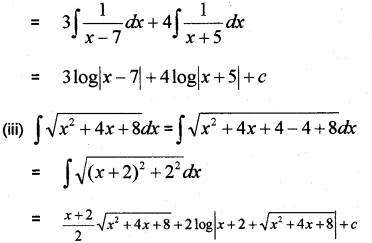
Question 2.
(i) Evaluate \(\int-\frac{\cos e c^{2} x}{\sqrt{\cot ^{2} x+9}} d x\)
(ii) Evaluate \(\int\left(\cos ^{-1} x\right)^{2} d x\) (May -2010)
Answer:

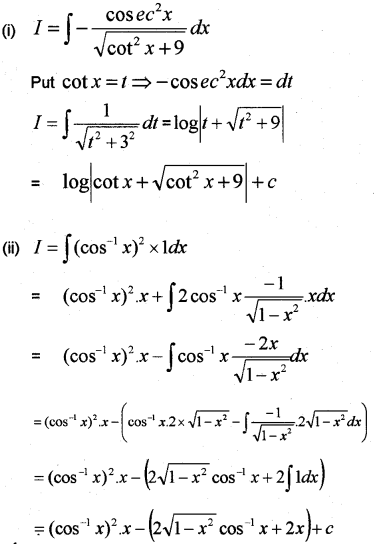
Question 3.
(i) Evaluate \(\int_{0}^{\pi} \frac{x \sin x}{1+\cos ^{2} x} d x\)
(ii) Evaluate \(\int_{0}^{2} e^{x} d x \text { as limit of a sum. }\) (May -2010)
Answer:

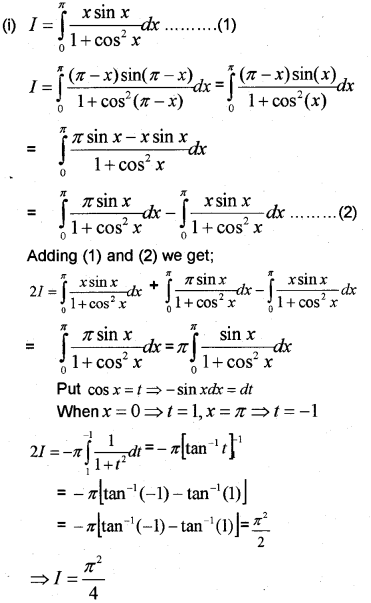
Question 4.
(i) Fill in the blanks \(\int \cot x d x=\)_____
(ii) Evaluate the integrals
\(\begin{array}{l}
\text { (a) } \int \sin 2 x \cos 4 x d x \\
\text { (b) } \int \frac{x}{(x+1)(x+2)} d x
\end{array}\) (March -2011)
Answer:

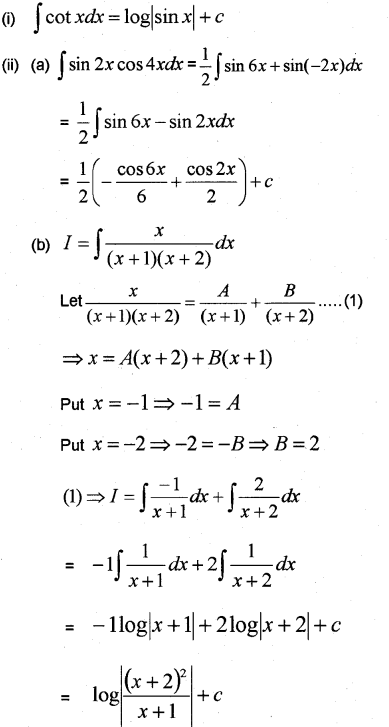
Question 5.
(i) Evaluate \(\int_{0}^{1} x d x\) as the limit of a sum.
(ii) Evaluate \(\int_{0}^{1} x(1-x)^{n} d x\) (March – 2011)
Answer:

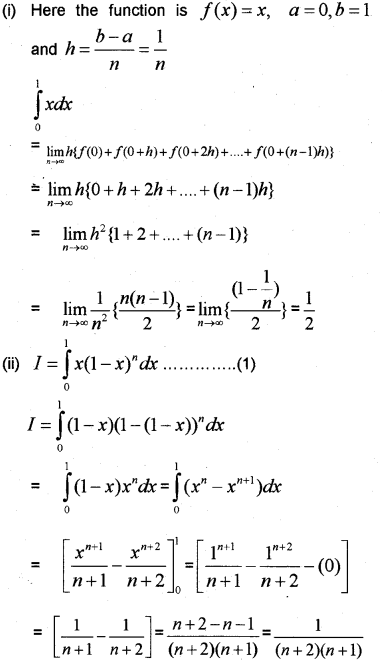
Question 6.
(i) Evaluate \(\int_{1}^{2} \frac{1}{x(1+\log x)^{2}} d x\)
(ii) Evaluate \(\int_{0}^{3}\left(2 x^{2}+3\right) d x\) as the limit of a sum. (May – 2011)
Answer:

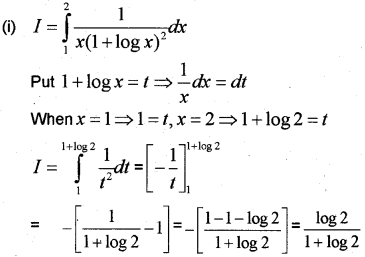
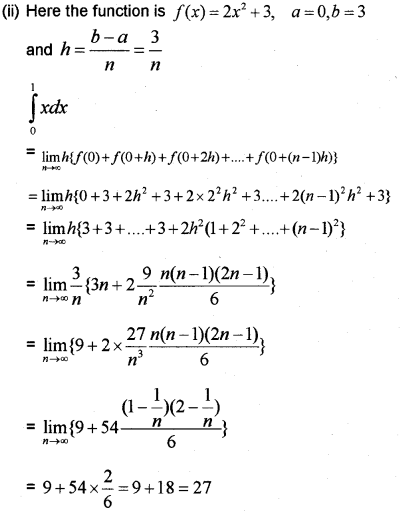
Question 7.
(i) What is \(\int \frac{1}{9+x^{2}} d x=?\)
(ii) Evaluate the integrals \(\int \frac{1}{1+x+x^{2}+x^{3}} d x\) (May – 2012)
Answer:

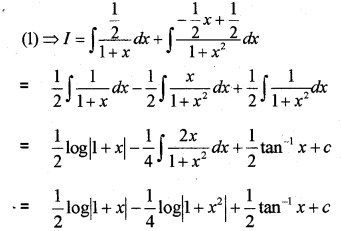
Question 8.
(i) Evaluate \(\int_{0}^{3} f(x) d x\)
where \(f(x)=\left\{\begin{array}{ll}
x+3, & 0 \leq x \leq 2 \\
3 x, & 2 \leq x \leq 3
\end{array}\right.\)

(ii) Prove that \(\int_{0}^{1} \log \left(\frac{x}{1-x}\right) d x=\int_{0}^{1} \log \left(\frac{1-x}{x}\right) d x\) Find the value of \(\int_{0}^{1} \log \left(\frac{x}{1-x}\right) d x\) (May – 2012)
Answer:

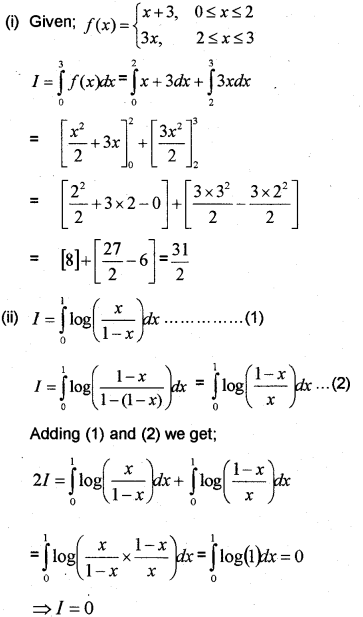
Question 9.
(i) Find \(\int \cot x d x=\ldots \ldots\)
(ii) Find \(\int x \log x d x\)
(iii) Find \(\int \frac{x-1}{(x-2)(x-3)} d x\) (March – 2013)
Answer:

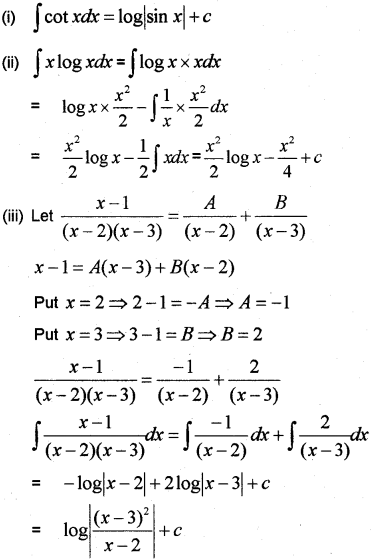
Question 10.
Evaluate
\(\text { (i) } \int \frac{x+3}{\sqrt{5-4 x-x^{2}}} d x\)
\(\text { (ii) } \int_{\pi / 6}^{\pi / 3} \frac{d x}{1+\sqrt{\tan x}}\) (May – 2013)
Answer:

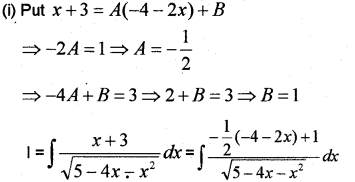
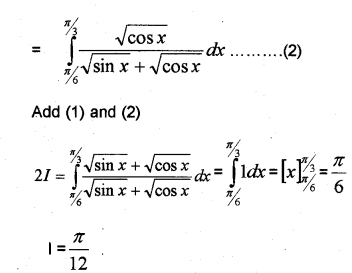
Question 11.
Evaluate
\(\begin{array}{l}
\text { (i) } \int x^{2} \tan ^{-1} x d x \\
\text { (ii) } \int_{-1}^{2} x^{3}-x d x
\end{array}\) (May – 2013)
Answer:

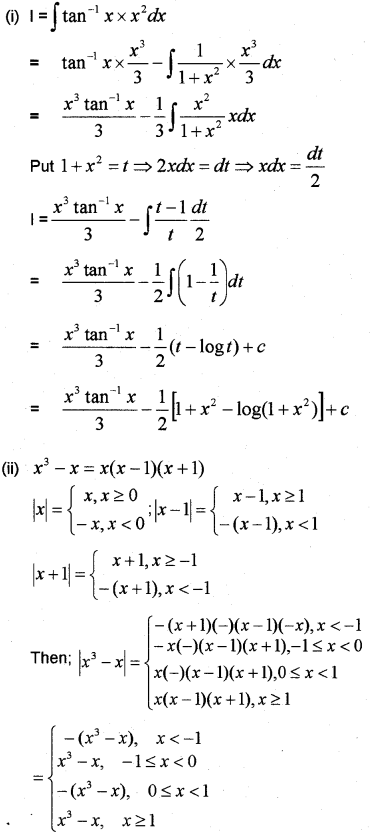
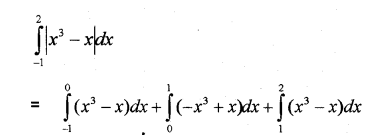
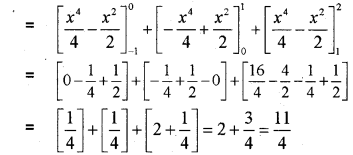
Question 12.
Evaluate \(\int_{0}^{\pi / 4} \log (1+\tan x) d x\) (March – 2013)
Answer:

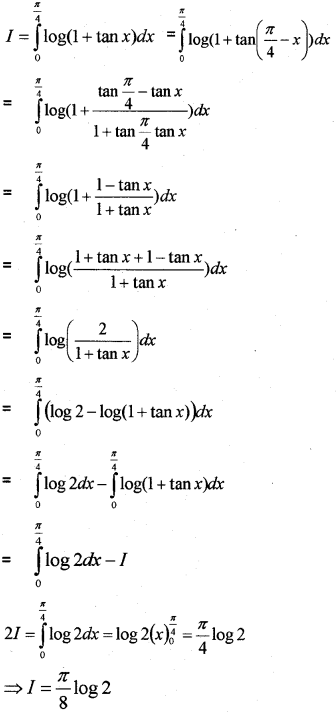
Question 13.
(a) The value of \(\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}} \cos x d x\) (May – 2014)
(b) Prove that \(\int_{0}^{\pi} \frac{x}{a^{2} \cos ^{2} x+b^{2} \sin ^{2} x} d x=\frac{\pi^{2}}{2 a b}\)
Answer:

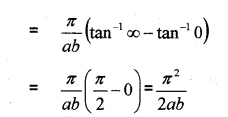
Question 14.
(a) \(\int \frac{1}{x^{2}+a^{2}} d x=\)
(b) Find \(\int \frac{1}{9 x^{2}+6 x+5} d x\)
(c) Find \(\int \frac{x}{(x-1)^{2}(x+2)} d x\) (May – 2014)
Answer:

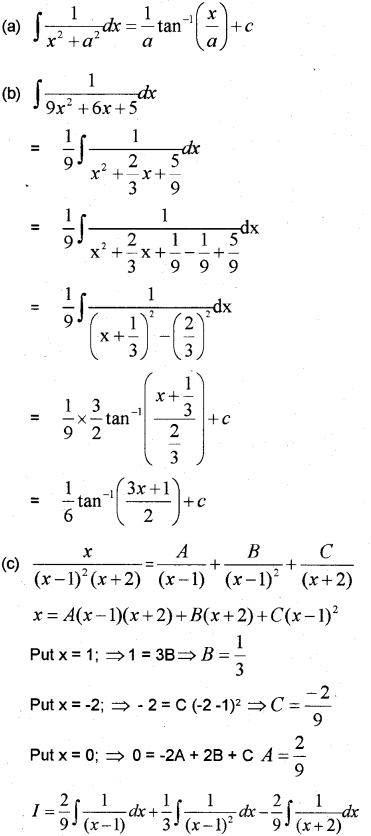
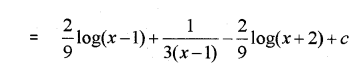
Question 15.
Integrate the following
\(\begin{array}{l}
\text { (a) } \frac{x-1}{x+1} \\
\text { (b) } \frac{\sin x}{\sin (x-a)} \\
\text { (c) } \frac{1}{\sqrt{3-2 x-x^{2}}}
\end{array}\) (March – 2015)
Answer:

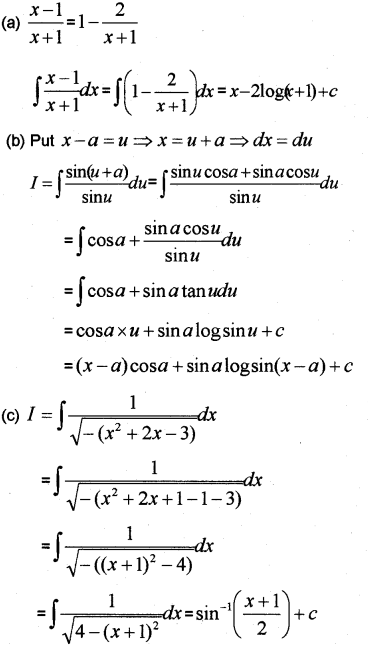
Question 16.
(a) Prove that \(\int \cos ^{2} x d x=\frac{x}{2}+\frac{\sin 2 x}{4}+c\)
(b)Find \(\int \frac{1}{\sqrt{2 x-x^{2}}} d x\)
(c) Find \(\int x \cos x d x\) (May – 2015)
Answer:

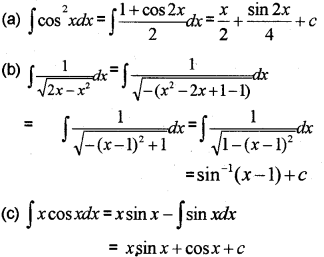
Question 17.
Find the following:
\(\begin{array}{l}
\text { (i) } \int \frac{1}{x\left(x^{7}+1\right)} d x \\
\text { (ii) } \int_{1}^{4}|x-2| d x
\end{array}\)
Answer:

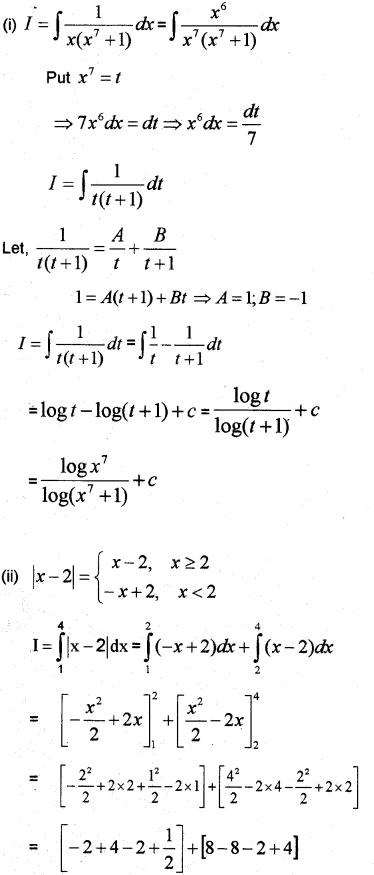
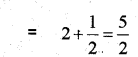
Question 18.
Find \(\int_{0}^{\frac{\pi}{2}} \log \sin x d x\)
Answer:

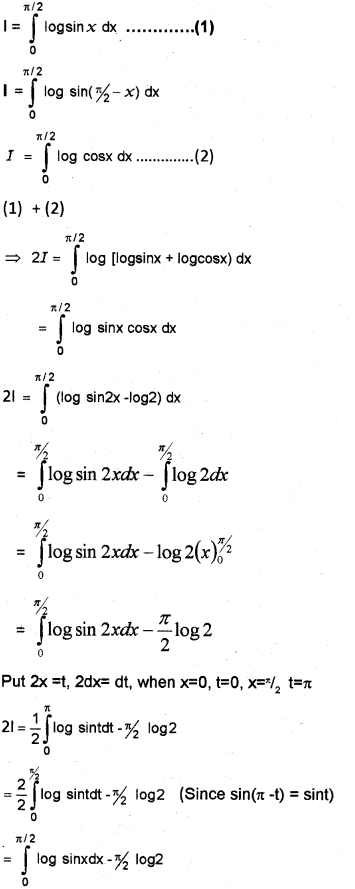
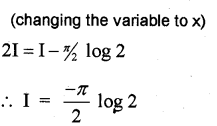
Question 19.
Find the following: \(\begin{array}{l}
\text { (i) } \int \cot x \log (\sin x) d x \\
\text { (ii) } \int \frac{1}{x^{2}+2 x+2} d x \\
\text { (iii) } \int x e^{9 x} d x
\end{array}\) (May – 2017)
Answer:

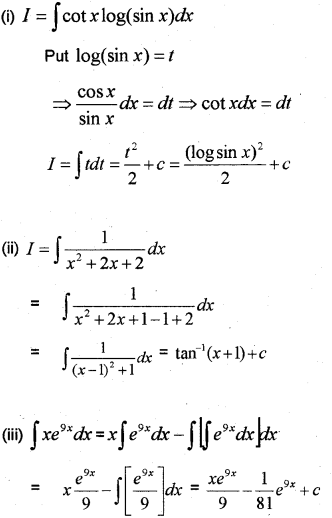
We hope the Plus Two Maths Chapter Wise Previous Questions Chapter 7 Integrals help you. If you have any query regarding Kerala Plus Two Maths Chapter Wise Previous Questions Chapter 7 Integrals, drop a comment below and we will get back to you at the earliest.