Plus Two Maths Chapter Wise Previous Questions Chapter 6 Application of Derivatives

Plus Two Maths Chapter Wise Previous Questions Chapter 6 Application of Derivatives are part of Plus Two Maths Chapter Wise Previous Year Questions and Answers. Here we have given Plus Two Maths Chapter Wise Previous Chapter 6 Application of Derivatives.

Kerala Plus Two Maths Chapter Wise Previous Questions Chapter 6 Application of Derivatives

Plus Two Maths Application of Derivatives 4 Marks Important Questions

Question 1.
(a) Find the equation of the tangent to the curve \(x^{\frac{2}{3}}+y^{\frac{2}{3}}=2\) at (1,1).
(b) Find two positive numbers whose sum is 15 and the sum of whose squares is minimum. (May – 2015)
Answer:

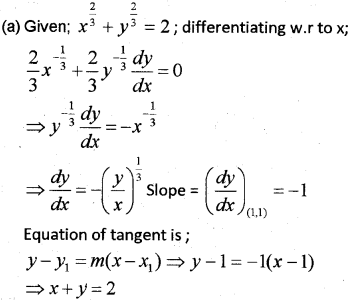
Question 2.
(a) The slope of the tangent to the curve given
\(x=1-\cos \theta, y=\theta-\sin \theta \text { by at } \theta=\frac{\pi}{2}\)
(i) 0
(ii) – 1
(iii) 1
(iv) Not defined.

(b) Find the intervals in which the function f(x) = x² – 4x + 6 is strictly decreasing.
(C) Find the minimum and maximum value, if any, of the function f(x) = (2x – 1)² + 3 (March – 2016)
Answer:
(a) (iii) 1
(b) Given; f(x) = x² – 4x + 6 ⇒ f’(x) = 2x – 4
For turning points; f’(x) = 2x – 4 0 ⇒ x = 2
So volurn.,e is niaxirnum when h = 2r
The intervals are (- ∞, 2); (2, ∞)
f’(0) = 2 x 0 – 4 = -4
Therefore f(x) is decreasing in (- ∞, 2)
(c) f(x) = (2 x 1)² + 3
⇒ f’(x) 2(2x – 1) x 2 f”(x) = 8
For tuming points; f’(x) = 8x – 4 = 0 ⇒ x = 1/2
f(x) has minimum value at x = 1/2 minimum value is \(f\left(\frac{1}{2}\right)=3\)
2)

Question 3.
(a) Which of the following function has neither local maxima nor local minima?
(i) f(x) = x² + x
(ii) f(x) = logx
(iii) f(x) = x³ – 3x + 3
(iv) f(x) = 3 + |x|
(b) Find the equation of the tangent to the curve y = 3x² at (1,1). (March – 2016)
Answer:

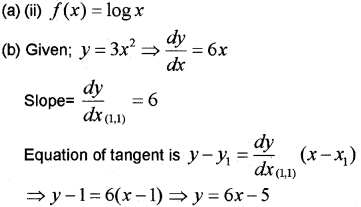
Question 4.
(i) The slope of the normal to the curve, y = x³ – x² at (1, -1) is
(a) 1
(b) – 1
(c) 2
(d)0

(ii) Find the intervals in which the function f(x) = 2x³ – 24x + 25 is increasing or decreasing. (May – 2016)
Answer:
(i) (b) – 1
(ii) f(x) = 2x³ – 24x + 25
f’(x) = 6x² – 24
f’(x) = O
⇒ 6x² – 24 = 0 ⇒ x² = 4 ⇒ x = – 2,2
Therefore the intervals are (-∞, -2); (-2, 2); (2, ∞)
f(x) is increasing in the intervals (-∞, -2); (2, ∞)
f(x) is decreasing in the intervals (-2, 2)

Question 5.
(i) The slope of the normal to the curve, y² – 4x at (1,2) is
(a) 1
(b) 1/2
(c) 2
(d) – 1

(ii) Find the intervals in which the function 2x³ + 9x² + 12x – 1 is strictly increasing. (March – 2017)
Answer:
(i) (b) – 1
(ii) f(x) = 2x³ + 9x² + 12x – 1
f’(x) = 6x² + 18x + 12
= 6(x² + 3x + 2) = 6(x + 1) (x + 2)
f’(x) = O
⇒ 6(x + 1)(x + 2) = 0 ⇒ x = – 1 – 2
Therefore the intervals are
(- ∞, – 2); (- 2, – 1); (- 1, ∞)
In the ¡nterval (- ∞, – 2)
f’( – 3) = 6(- 3 + 1) (- 3 + 2) > 0
Therefore increasing In the interval (- 2, – 1)
f’(- 1.5) = 6(- 1.5 + 1)(- 1.5 + 2) < 0
Therefore decreasing In the interval (- 1, ∞)
f’(0) = 6(0 + 1)(0 + 2) > 0
Therefore increasing

Question 6.
Find two positive numbers whose sum is 16 and sum of whose cubes is minimum. (March – 2017)
Answer:
Let the numbers be x and 16 – x. Then,
S = x³ + (16 – x)³
= S’ = 3x² + 3(16 – x)²(- 1)
⇒ S” = 6x + 6(16 – x)………..(1)
For turning points S’ = 0 ⇒ 3 x² – 3(16 – x)² = 0
⇒ x² – 16 + 32x – x² =0
⇒ – 16² + 32x = 0 = x² = \(\frac{16 \times 16}{32}\) =8
(1) ⇒ S” = 6(8) + 6(16 – 8) > 0
TherefocemrnimumM x = 8
Thusthe numbers are8 and 16 – 8 = 8

Plus Two Maths Application of Derivatives 6 Marks Important Questions

Question 1.
(i) Show that the function x³ – 6x² + 15x + 4 is strictly increasing in R.
(ii) Find the approximate change in volume of a cube of side x meters caused by an increase in the side by 3%.
(iii) Find the equation of the tangent and normal at the point (1,2) on the parabola y² = 4x. (March – 2010)
Answer:
(i) Given; f(x) = x³ – 6x² + 15x + 4
f’(x) = 3x² – 12x + 15 = 3(x² – 4x +5)
= 3(x² – 4x + 4 + 1) = 3(x – 2)² + 1) > 0
For any value of x, f(x) is a strKly ¡ncreasing.

(ii) We have; V = x³ and Δx = 3% of x = 0.03x
\(d V=\frac{d V}{d x} \Delta x=3 x^{2} \Delta x\)
= 3x² x 0.03x = 0.09x³ = 0.09V
\(\Rightarrow \frac{d V}{V}=0.09\)

Therefore 9% is the approximate increase In volume.

(iii) Given; y²….4x ⇒ 2y \(\frac{d y}{d x}\) = 4 ⇒ \(\frac{d y}{d x}=\frac{2}{y}\)
Slope at (1,2) = \(\frac{2}{2}\) = 1
Equation of tangent at (1,2) is; y – 2 = 1(x – 1)
⇒ x – y + 1 = 0
Equation of normal at (1,2) is; y – 2 = – 1(x – 1)
⇒ x + y – 3 = 0

Question 2.
Consider the parametric forms
x = 1 + \(\frac{1}{t}\) – and y = t – \(\frac{1}{t}\) ofa curve
(i) Find \(\frac{d y}{d x}\)
(ii) Find the equation of the tangent at t = 2.
(iii) Find the equation of the normal at t = 2. (May – 2010)
Answer:

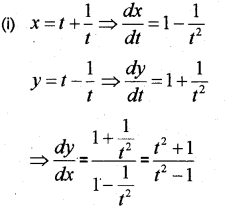
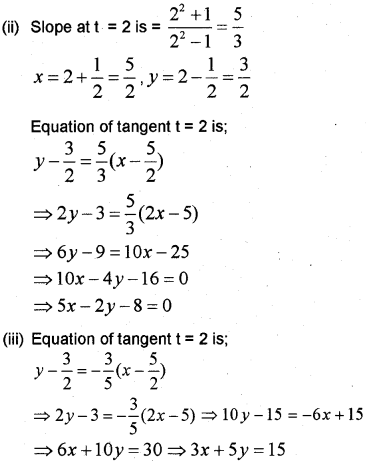
Question 3.
(i) The radius of a circle is increasing at the rate of 2cmls. Find the rate at which area of the circle is increasing when radius is
6cm.
(ii) Prove that the function f(x) = log sin x is strictly increasing in \(\left(0, \frac{\pi}{2}\right)\) and strictly decreasing in \(\left(\frac{\pi}{2}, \pi\right)\)
(iii) Find the maximum and minimum value of the function f(x) = x³ – 6x² + 9x + 15. (March – 2011)
Answer:

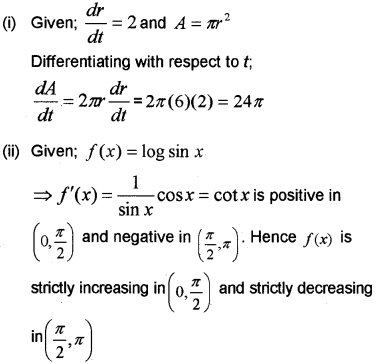
Question 4.
(i) Find the approximate value of (82)^1/4 up to three places of decimals using differentiation.
(ii) Find two positive numbers such that Their sum is 8 and the sum of their squares is minimum. (May – 2011)
Answer:

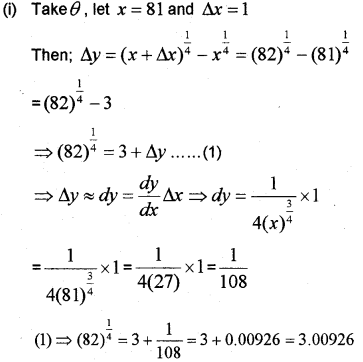
(ii) Let the numbers be x and 8 – x. Then,
S = x² + (8 – x)²
⇒ S’ = 2x + 2(8 – x)( – 1)
⇒ S” = 2 + 2 = 4 ………..(1)
For turning points S’ = 0 = 2x – 2(8 – x) = 0
⇒ 4x – 16 = 0 ⇒ x = 4
(1) ⇒ S” = 4 > 0
Therefore minimum at x = 4
Thus the numbers are 4 and 8 – 4 = 4.

Question 5.
(i) The slope of the tangent to the curve y = x³ – 1 at x = 2 is ……….
(ii) Use differentiation to approximate \(\sqrt{36.6}\)
(iii) Find two numbers whose sum is 24 and whose product as large as possible. (March – 2012, March – 2016)
Answer:

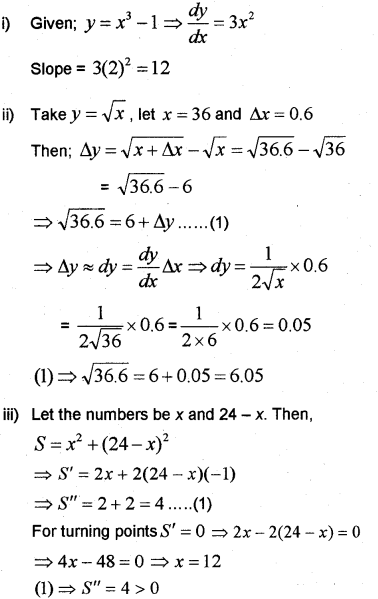
Therefore minimum at x =12
Thus the numbers are 12 and 24 – 12 = 12.

Question 6.
(i) Show that the function x³ – 3x² + 6x – 5 is strictly increasing on R.
(ii) Find the interval in which the function f(x) = sin x + cosx; 0 < x < 2π is strictly increasing or strictly decreasing. (May – 2012)
Answer:
(i) Given; f(x) = x³ – 3x² + 6x – 5
f’(x) = 3x² – 6x + 6 = 3(x² – 2x +2)
= 3(x² – 2x + 1 + 1) 3(x – 1)² + 1) > 0
For any value cit x, f(x) is a strictly increasing.

Question 7.
(i) Find the slope of the normal to the curve y = sinθ at θ = π/4
(ii) Show that the function f(x) = x³ – 6x² + 15x + 4 is strictly increasing in R.
(iii) Show that all rectangles with a given perimeter, the square has the maximum area. (March – 2013)
Answer:

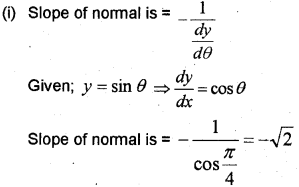
(ii) f(x) = x³ – 6x² + 15x + 4
Differentiating w.r.t x;
f(x) = 3x² – 12x + 15 = 3(x² – 4x + 5)
= 3 (x² – 4x + 4 + 1)
= 3 ((x – 2)² + 1) > 0, ∀x∈R
Therefore fis strictly increasing in R.

(iii) Let x and ybe the length and breadth of a rectangle with area A and perimeter P.

Question 8.
A right circular cylinder is inscribed in a given cone of radius R cm and height H cm as shown in the figure.

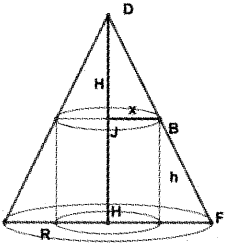
(i) Find the Surface Area S of the circular cylinder as a function of x.
(ii) Find a relation connecting x and R when S is a maximum. (May – 2013)
Answer:
(i) There are two similar triangles ΔDJB and ΔDHF

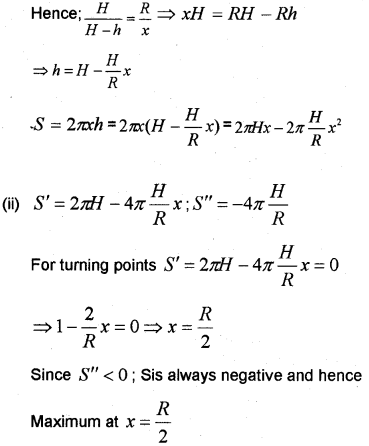
Question 9.
(i) Which of the following function is Increasing for all values of x in its domain?
(a) sin x
(b) log x
(c) x²
(d) |x|

(ii) Find a point on the curve y = (x – 2)² at which the tangent is parallel to the chord joining the points (2,0) and (4,4).
(iii) Find the maximum profit that a company can make, if the profit function is given by p(x) = 41 – 24x – 6x². (March – 2014)
Answer:
(i) (b) log x
(ii) Given; y = (x – 2)² ⇒ \(\frac{d y}{d x}\) = 2(x – 2)
Slope of the chord = \(\frac{4-0}{4-2}=2\)
\(\Rightarrow 2=2(x-2) \Rightarrow x=3 \Rightarrow y=(3-2)^{2}=1\)
Therefore the required point is (3, 1)

(iii) Given; p(x) = 41 – 24x – 6x²
p’(x) = – 24 – 12x
p”(x) = – 12
For turning points p’(x) = – 24 – 12x = 0
⇒ x = -2
Since p”(x) = – 12 always maximum Therefore maximum value p(- 2) = 41 – 24(- 2) 6(- 2)² = 65

Question 10.
(a) Find the slope of the tangent to the parabola y² = 4ax at (at², 2at).
(b) Find the intervals in which the function x² – 2x + 5 is strictly increasing.
(c) A spherical bubble volume at the rate of which the diminishing when the is decreasing in 2cm³/sec. Find the surface area is radius is 3cm. (May – 2014)
Answer:

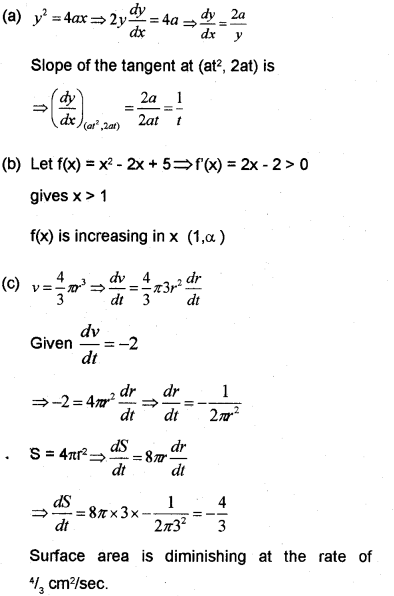
Question 11.
(a) Which of the following function is always increasing?
(i) x + sin 2x
(ii) x – sin 2x
(ill) 2x + sin 3x
(iv) 2x – sin 2x
(b) The radius of a cylinder is increasing at a rate of 1cm/s and its height decreasing at a rate of 1cm/s. Find the rate of change of its volume when the radius is 5cm and the height is 5cm.
(c) Write the equation of tangent at (1,1) on the curve 2x² + 3y² = 5. (March – 2015)
Answer:

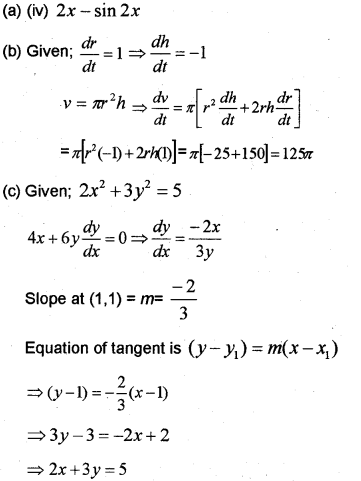
We hope the Plus Two Maths Chapter Wise Previous Questions Chapter 6 Application of Derivatives help you. If you have any query regarding Kerala Plus Two Maths Chapter Wise Previous Questions Chapter 6 Application of Derivatives, drop a comment below and we will get back to you at the earliest.