Plus Two Maths Chapter Wise Previous Questions Chapter 5 Continuity and Differentiability

Plus Two Maths Chapter Wise Previous Questions Chapter 5 Continuity and Differentiability are part of Plus Two Maths Chapter Wise Previous Year Questions and Answers. Here we have given Plus Two Maths Chapter Wise Previous Chapter 5 Continuity and Differentiability.

Kerala Plus Two Maths Chapter Wise Previous Questions Chapter 5 Continuity and Differentiability

Plus Two Maths Continuity and Differentiability 3 Marks Important Questions

Question 1.
Consider \(f(x)=\left\{\begin{array}{ll}
\frac{x^{2}-x-6}{x+2}, & x \neq-2 \\
-5, & x=-2
\end{array}\right.\)

(i) Find f(-2)
(ii) Check whether the function f(x) is continuous at x= -2. (March – 2009)
Answer:

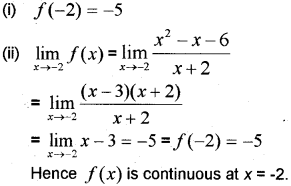
Question 2.
If f(x) = sin(Log x), prove that x² y₂ + xy₁ + y = 0 (May -2009)
Answer:
Given; y sin(Iogx)
Differentiating with respect to X;
\(y_{1}=\cos (\log x) \frac{1}{x} \Rightarrow x y_{1}=\cos (\log x)\)
Again differentiating with respect to x
\(\begin{array}{l}
\Rightarrow x y_{2}+y_{1}=-\sin (\log x) \frac{1}{x} \\
\Rightarrow x^{2} y_{2}+x y_{1}=-y \Rightarrow x^{2} y_{2}+x y_{1}+y=0
\end{array}\)

Question 3.
(i) Establish that g(x) =1 – x + |x| is continuous at origin.
(ii) Check whether h(x) = |l – x + |x|| is continuous at origin. (March – 2010)
Answer:
(i) Given; g(x) = 1 – x + |x| ⇒ g(x) (1 – x) + |x|
Here g(x) is the sum of two functions continuous functions hence continuous.
(ii) We have;
\(\begin{array}{l}
f o g(x)=f(g(x)) \\
=\quad f(1-x+|x|)=|1-x+| x \mid=h(x)
\end{array}\)
The composition of two continuous functions is again continuous. Therefore h(x) continuous.

Question 4.
Find \(\frac{d y}{d x}\) of the following
\(\begin{array}{l}
\text { (i) } x=\sqrt{a^{\sin ^{4} 4}} \quad y=\sqrt{a^{\cos ^{-1} t}} \\
\text { (ii) } y=\cos ^{-1} \frac{\left(1-x^{2}\right)}{\left(1+x^{2}\right)}, 0<x<1 \\
\text { (iii) } y=\sin ^{-1} 2 x \sqrt{1-x^{2}}, y_{\sqrt{2}}<x<y_{\sqrt{2}}
\end{array}\)
Answer:

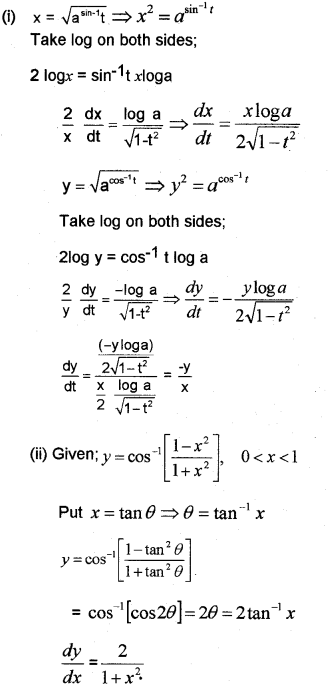
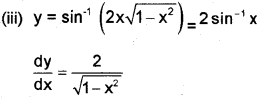
Question 5.
Find \(\frac{d y}{d x} \text { if } x^{3}+2 x^{2} y+3 x y^{2}+4 y^{3}=5\) (March – 2015)
Answer:

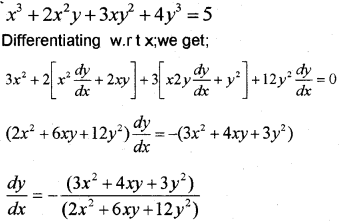
Question 6.
Find all points of discontinuity of f where f is defined by \(f(x)=\left\{\begin{array}{ll}
2 x+3, & x \leq 2 \\
2 x-3, & x>2
\end{array}\right.\) (March – 2016)
Answer:
In both the intervals x \(\leq[latex] 2 and x > 2 the function f(x) is a polynomial so continuous. So we havetocheckthe continuity at x = 2.

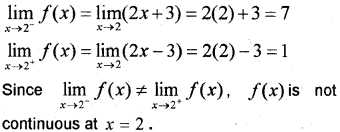
Question 7.
If e^x-y = x^y, then prove that [latex]\frac{d y}{d x}=\frac{\log x}{[\log \operatorname{ex}]}\) (May – 2014; March – 2016)
Answer:

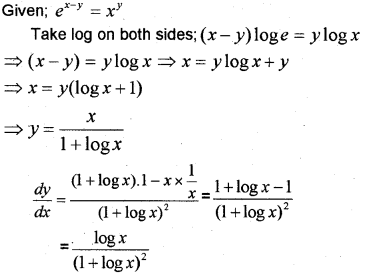
Plus Two Maths Continuity and Differentiability 4 Marks Important Questions

Question 1.
Find \(\frac{d y}{d x}\) of the following (March – 2009)
\(\begin{array}{l}
\text { (i) } y=\sin ^{-1}\left(3 x-4 x^{3}\right)+\cos ^{-1}\left(4 x^{3}-3 x\right) \\
\text { (ii) } y=\tan ^{-1}\left(\sqrt{\frac{1-\cos x}{1+\cos x}}\right)
\end{array}\)
Answer:

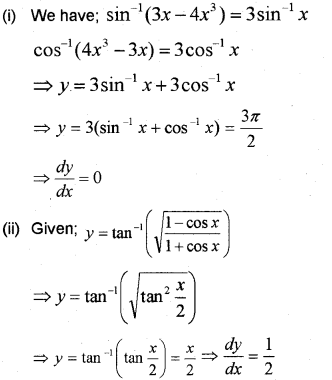
Question 2.
Consider the function f(x) = |x| x ∈ R
(i) Draw the graph of f(x) =|x|
(ii) Show that the function is continuous at x = 0. (March – 2010)
Answer:

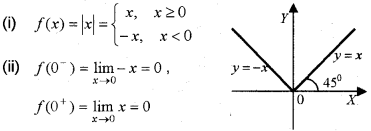
f(0^–) f(0^–) = 0. therefore continuous at x = 0.
AIso from the figure we can see that the graph does not have a break or jump.

Question 3.
(i) Find the derivative of y = x^a + a^x with respect to x.
(ii) If e^y (x + 1) = 1 , showthat \(\frac{d^{2} y}{d x^{2}}=\left(\frac{d y}{d x}\right)^{2}\) (May – 2011)
Answer:

Question 4.
(i) Check the continuity of the function given by f(x) \(f(x)=\left\{\begin{array}{ll}
x \sin \frac{1}{x}, & x \neq 0 \\
1, & x=0
\end{array}\right.\)

(ii) Verify Mean Value Theorem for the function f(x) = x + 1/x in the interval [1,3]. (May – 2011)
Answer:


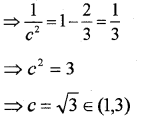
Hence Mean Value Theorem ¡s verified.

Question 5.
(i) Determine the value of k so that the function (May – 2012)

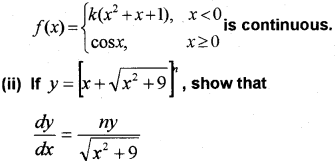
Answer:

Question 6.
Consider a fUnction f: R → R defined by
\(f(x)=\left\{\begin{array}{cc}
a+x, & x \leq 2 \\
b-x, & x>2
\end{array}\right.\)

(i) Find a relation between a and b if f is continuous at x = 2.
(ii) Find a and b, if f is continuous at x2 and a + b = 2. (May – 2013)
Answer:
(i) Since fis continuous at x = 2, we have;

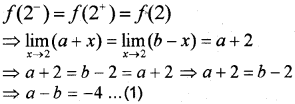
(ii) Given a = 2 …(2) Solving (1) and (2) we have;
⇒ 2a = – 2 ⇒ a = – 1
⇒ b = 2 – a = 2 + 1 = 3

Question 7.
(i) Find if x = a(t – sin t) y = a(1 + cos t)
(ii) Verify Rolles theorem for the function f(x) = x2 + 2 in the interval [-2, 2] (March – 2014)
Answer:

Question 8.
(a) Find the relationship between a and b so that the function f defined by
\(f(x)=\left\{\begin{array}{ll}
a x^{2}-1, & x \leq 2 \\
b x+3, & x>2
\end{array}\right.\) is continuous.

(b) Verify mean value theorem for the function f(x) = x2 – 4x -3 ¡n the interval [1, 4]. (May – 2014)
Answer:
(a) Since fis continuous

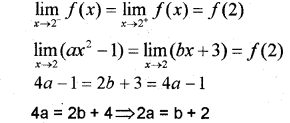
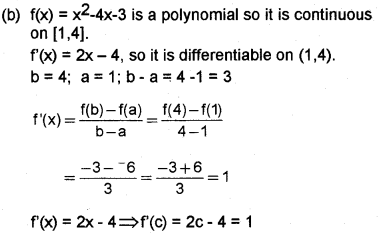
Hence mean value theorem satisfies for the funcion.

Question 9.
(a) Find ‘a’ and ‘b’ if the function
\(f(x)=\left\{\begin{array}{ll}
\frac{\sin x}{x}, & -2 \leq x \leq 0 \\
a \times 2^{x}, & 0 \leq x \leq 1 \\
b+x, & 1<x \leq 2
\end{array}\right.\) is continous on [-2, 2]

(b) How many of the functions
f(x) = |x|, g(x) = |x|², h(x) = |x|³ are not differentiable at x = 0?
(i) 0
(ii) 1
(iii) 2
(iv) 3 (March – 2015)
Answer:
(a) Since f(x) is continuous on [-2, 2]

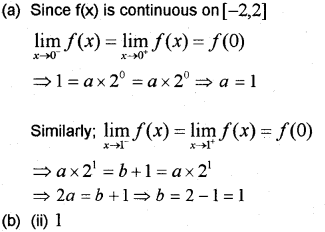
Question 10.
(a) Find the relation between ‘a’ and ‘b’ if the function f defined by
\(f(x)=\left\{\begin{array}{l}
a x+1, x \leq 3 \\
b x+3, x>3
\end{array}\right.\) is continuous.
lbx+3.x>3
(b) If e^y (x + 1) = 1, show thats \(\frac{d^{2} y}{d x^{2}}=\left(\frac{d y}{d x}\right)^{2}\) (May -2015)
Answer:

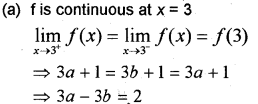
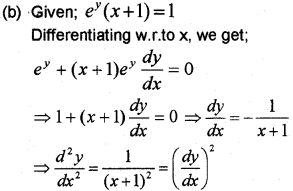
Question 11.
Find the value of a and b such that the function \(f(x)=\left\{\begin{array}{cc}
5 a & x \leq 0 \\
a \sin x+\cos x & 0<x<\frac{\pi}{2} \\
b-\frac{\pi}{2} & x \geq \frac{\pi}{2}
\end{array}\right.\) is continuous. (March – 2010)
Answer:

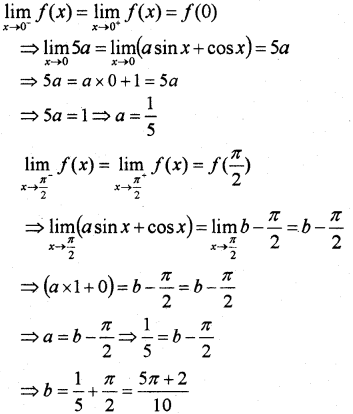
Question 12.
(i) Find \(\frac{d y}{d x}, \text { if } x=a \cos ^{2} \theta ; y=b \sin ^{2} \theta\)
(ii) Find the second derivative of the function y = e^x sinx. (May – 2017)
Answer:

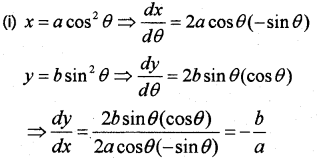
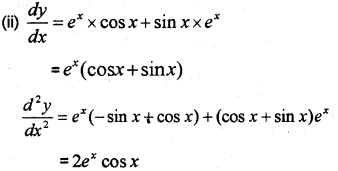
Question 13.
Find \(\frac{d y}{d x}\) of the following (4 score each)
(i) y^x = x^y (May – 2015)
(ii) (COSx)^y = (cosy)^x (March – 2017)
Answer:

Plus Two Maths Continuity and Differentiability 6 Marks Important Questions

Question 1.
Find \(\frac{d y}{d x}\) if
(i) sinx + cosy = xy
(ii) x = acos³t, y = asin³t
(iii) y = x^x + (logx)^x (May -2009; May -2011; March -2015)
Answer:
(i) Given; sinx + cosy = xy
Differentiating with respect to x;

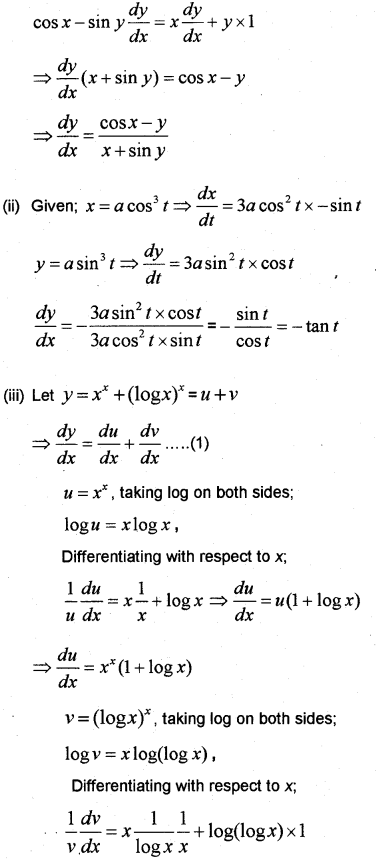
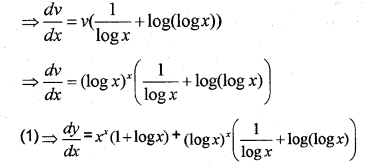
Question 2.
(i) Let y =3 cos(log x) + 4 sin (log x)
(a) Find \(\frac{d y}{d x}\)
(b) Prove that x² y₂ + xy₁ + y = 0

(ii) (a) Find the derivative of y = e^2x+logx
(b) Find \(\frac{d y}{d x}\)
if x = a (θ – sinθ), y = a(1 – cosθ) (March – 2009)
Answer:

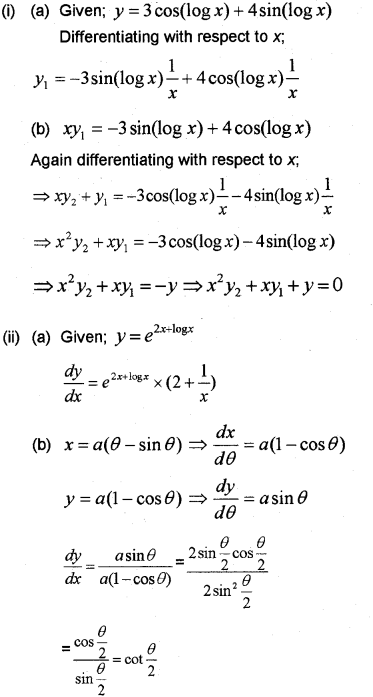
Question 3.
(i) Show that the function f (x) defined by f(x) = sin (cosx) is a continuous function.
(ii) If \(\frac{d y}{d x}=\frac{1}{\frac{d x}{d y}}\), Show that \(\frac{d^{2} y}{d x^{2}}=\frac{-\frac{d^{2} x}{d y^{2}}}{\left(\frac{d x}{d y}\right)^{3}}\) (May -2010)
Answer:
Given; f(x) = sin(cos x)
Let g(x) = sin(x) and h(x) = cos x
Both these function are trigonometric functions hence continuous.
goh(x) = g(h(x)) = g(cos x) = sin(cos x) = f(x)

Since f(x) is the composition of two continuous functions, hence continuous.

Question 4.
(i) Let y = x^{sin x} + (sinx)^x. Find \(\frac{d y}{d x}\)
(ii) Given; \(y=\sqrt{\tan ^{-1} x}\)
(a) \(2\left(1+x^{2}\right) y \frac{d y}{d x}=1\)
(b) \(\left(1+x^{2}\right) y \frac{d^{2} y}{d x^{2}}+\left(1+x^{2}\right)\left(\frac{d y}{d x}\right)^{2}+2 x y \frac{d y}{d x}=0\) (May – 2010; Onam – 2017)
Answer:

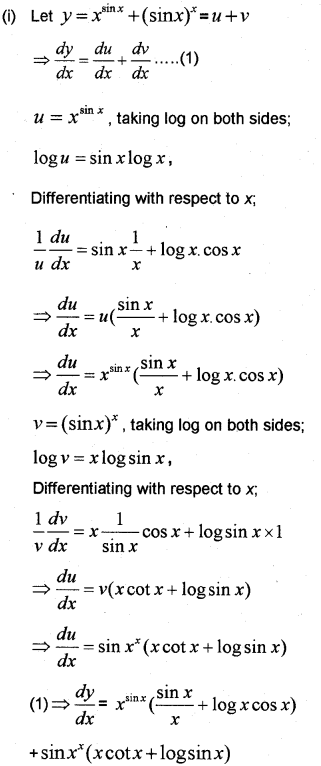
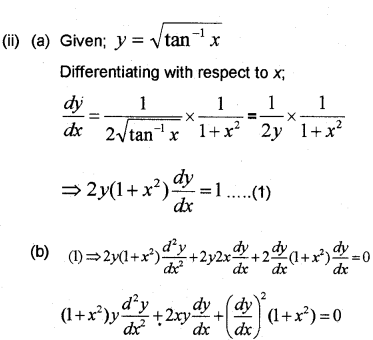
Question 5.
(i) The function \(f(x)=\left\{\begin{array}{ll}
5, & x \leq 2 \\
a x+b, 2< & x<10 \text { is } \\
21, & x \geq 10
\end{array}\right.\) continuous. Find a and b
(ii) Find \(\frac{d y}{d x}\) (a) if y = Sin (xsinx)
(iii) If y = ae” + be’; show that \(\frac{d^{2} y}{d x^{2}}-(m+n) \frac{d y}{d x}+m n y=0\) (March – 2011)
Answer:

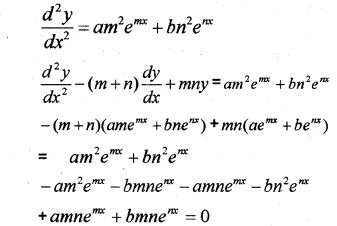
Question 6.
(i) Match the following.

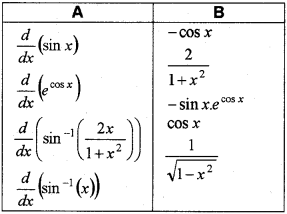
(ii) If y = sin^-1 x, prove that (1 – x²) y₂ – xy₁ = 0 (March – 2012; May -2017)
Answer:

Question 7.
(i) Consider \(f(x)=\left\{\begin{array}{ll}
3 x-8, & x \leq 5 \\
2 k, & x>5
\end{array}\right.\) Find the value of k if f(x) is continuous at x = 5.
(ii) Find \(\frac{d y}{d x}, \text { if } y=(\sin x)^{\log x}, \sin x>0\)
(iii) If y = (sin-1 x)2, then show that \(\left(1-x^{2}\right) \frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}=2\). (March -2013)
Answer:

Question 8.
(i) Find, if y = 1ogx, x>0
(ii) Is f(x) = |x| differentiable at x = 0?
(iii) Find if x = sin θ – cos θ and y= sinθ + cosθ (May – 2013)
Answer:

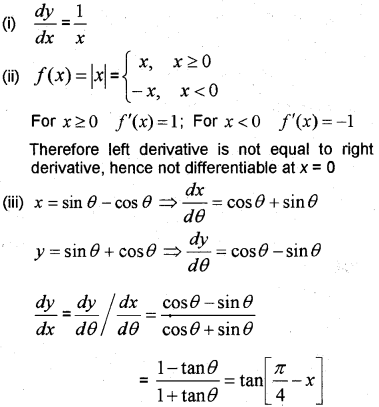
We hope the Plus Two Maths Chapter Wise Previous Questions Chapter 5 Continuity and Differentiability help you. If you have any query regarding Kerala Plus Two Maths Chapter Wise Previous Questions Chapter 5 Continuity and Differentiability, drop a comment below and we will get back to you at the earliest.