Plus Two Maths Chapter Wise Previous Questions Chapter 3 Matrices

Plus Two Maths Chapter Wise Previous Questions Chapter 3 Matrices are part of Plus Two Maths Chapter Wise Previous Year Questions and Answers. Here we have given Plus Two Maths Chapter Wise Previous Chapter 3 Matrices.

Kerala Plus Two Maths Chapter Wise Previous Questions Chapter 3 Matrices

Plus Two Maths Matrices 3 Marks Important Questions

Question 1.
Write A as the sum of a symmetric and a skew-symmetric matrix. $A=\left[\begin{array}{ccc} 1 & 4 & -1 \\ 2 & 5 & 4 \\ -1 & -6 & 3 \end{array}\right]$ (March – 2010)
Answer:

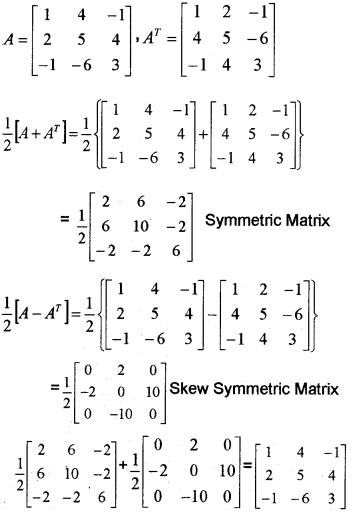
Question 2.
Consider the matrices
$A=\left[\begin{array}{lll} 2 & 1 & 3 \\ 2 & 3 & 1 \\ 1 & 1 & 1 \end{array}\right] \text { and } B=\left[\begin{array}{ccc} -1 & 2 & 3 \\ -2 & 3 & 1 \\ -1 & 1 & 1 \end{array}\right]$
(i) Find A+B
(ii) Find (A + B) (A-B) (May -2010)
Answer:

Question 3.
Given $P=\left[\begin{array}{cc} 2 & -3 \\ -1 & 2 \end{array}\right]$ Find the inverse of P by elementary row operation. (March 2011)
Answer:

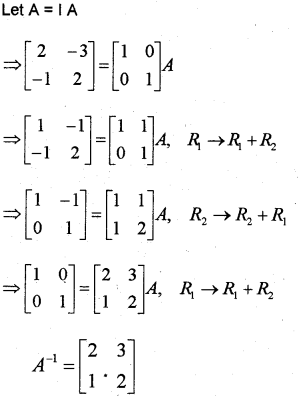
Question 4.
Let $A=\left[\begin{array}{lll} 3 & 6 & 5 \\ 6 & 7 & 8 \end{array}\right] \text { and } C=\left[\begin{array}{ccc} 1 & 2 & -3 \\ 4 & 5 & 6 \end{array}\right]$

(i) Find 2A
(ii) Find the matrix B such that 2A + B = 3C (May 2011)
Answer:

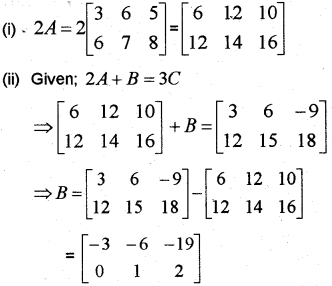
Question 5.
Let $A=\left[\begin{array}{cc} 2 & 4 \\ -1 & 1 \end{array}\right]$
(i) Apply elementary transformation R → R R1/2 in the matrix A.
(ii) Find the inverse of A by the elementary transformation. (May 2011)
Answer:

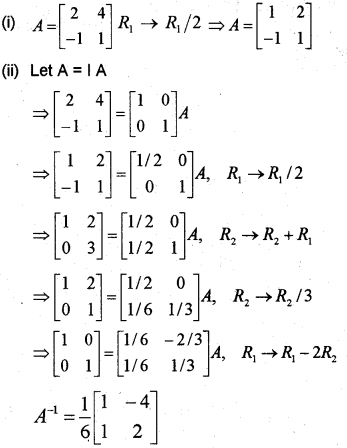
Question 6.
Consider the matrix $A=\left[\begin{array}{cc} 3 & 1 \\ -1 & 2 \end{array}\right]$
(i) Find A²
(ii) Find ksothat A2 = kA – 7I (March – 2012)
Answer:

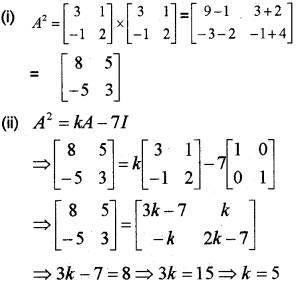
Question 7.
Consider a 2×2 matrix
$A=\left[a_{i j}\right]$ where $a_{i j}=|2 i-3 j|$
(i) Write A
(ii) Find A + A^T (March – 2012)
Answer:

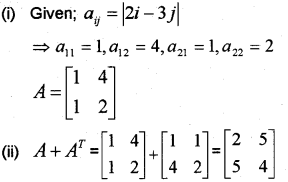
Question 8.
If $A=\left[\begin{array}{cc} 3 & 1 \\ -1 & 2 \end{array}\right]$ then
(i) Find A²
(ii) Hence show that A² – 5A + 7I = 0. (March 2013)
Answer:

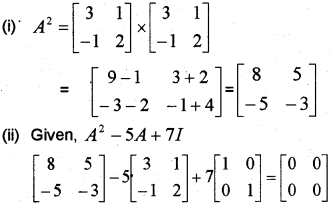
Question 9.
If a matrix $A=\left[\begin{array}{ll}3 x & x \\ -x & 2 x\end{array}\right]$ is a solution of the equation x² – 5x + 7 = 0, find any one value of X. (May 2013)
Answer:

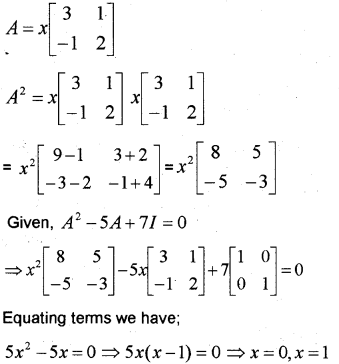
Question 10.
Consider the matrices $A=\left[\begin{array}{cc}1 & -2 \\ -1 & 3\end{array}\right]$ and $B=\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]$$ $A B=\left[\begin{array}{ll}2 & 9 \\ 5 & 6\end{array}\right]$, find the values of a,b,c,d (March – 2014)
Answer:

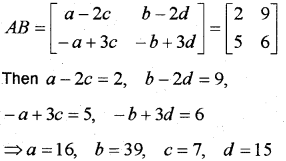
Question 11.
Consider a 2 x 2 matrix A=[a_ij] Where $a_{i j}=\frac{(i+2 j)^{2}}{2}$
(i) Write A
(ii) Find A + A^T (March – 2014)
Answer:

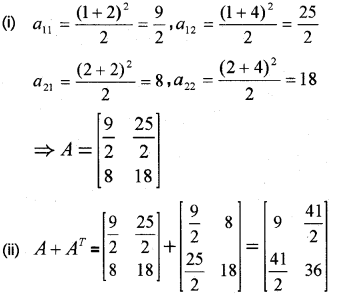
Question 12.
If X + Y = $\left[\begin{array}{ll}7 & 0 \\ 2 & 5\end{array}\right]$ and X – Y = $\left[\begin{array}{ll}3 & 0 \\ 0 & 3\end{array}\right]$ then
(i) Find X and Y.
(ii) Find 2X + Y. (May – 2014)
Answer:

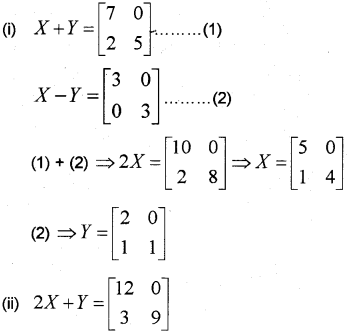
Question 13.
i) If A, B are symmetric matrices of same order then AB – BA is always a ………….
A) Skew-Symmetric matrix
B) Symmetric matrix
C) Identity matrix
D) Zero matrix
(ii) For the matrix $A=\left[\begin{array}{ll}2 & 4 \\ 5 & 6\end{array}\right]$, verify that A + A^T is a symmetric matrix. (March – 2015)
Answer:

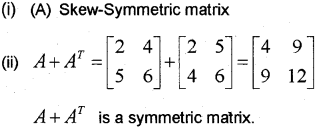
Question 14.
Consider the matrix $A=\left[\begin{array}{ll}3 & -2 \\ 4 & -2\end{array}\right]$
(i) Find A²
(ii) Find k so that A² = kA – 21 (May – 2015)
Answer:

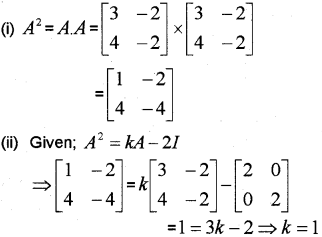
Plus Two Maths Matrices 4 Marks Important Questions

Question 1.
(i) Find the value of x and y from the equations $a\left[\begin{array}{cc}x & 5 \\ 7 & y-3\end{array}\right]+\left[\begin{array}{cc}3 & -4 \\ 1 & 2\end{array}\right]=\left[\begin{array}{cc}7 & 6 \\ 15 & 14\end{array}\right]$
(ii) Given $A=\left[\begin{array}{cc}1 & 2 \\ 3 & -1 \\ 4 & 2\end{array}\right], B=\left[\begin{array}{ccc}-1 & 4 & -5 \\ 2 & 1 & 0\end{array}\right]$ Show that AB ≠ BA (March – 2011)
Answer:

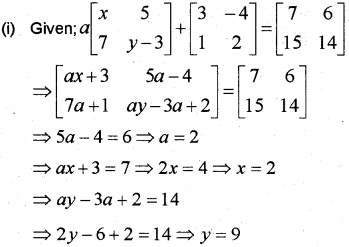
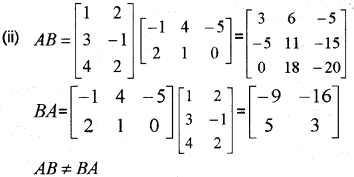
Question 2.
(i) Find a, b matrix $\left[\begin{array}{ccc}0 & 3 & a \\ b & 0 & -2 \\ 5 & 2 & 0\end{array}\right]$ is skew symmetric matrix.
(ii) Express $A=\left[\begin{array}{ccc}7 & 3 & -5 \\ 0 & 1 & 5 \\ -2 & 7 & 3\end{array}\right]$ sum of a symmetric and a skew symmetric matrix. (May – 2012)
Answer:

Question 3.
Consider the matrices $A=\left[\begin{array}{cc}2 & -6 \\ 1 & 2\end{array}\right]$ and $A+3 B=\left[\begin{array}{cc}5 & -3 \\ -2 & -1\end{array}\right]$
(i) Find matrix B
(il) Find matrix AB.
(iii) Find the transpose of B. (May – 2013)
Answer:

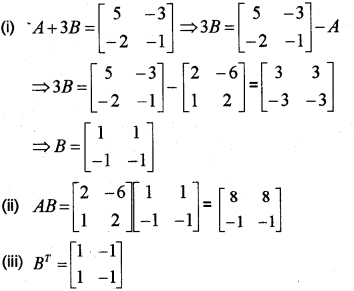
Question 4.
(i) The value of k such that matrix $\left[\begin{array}{cc} 1 & k \\ -k & 1 \end{array}\right]$ is symmetric if
(a) 0
(b) 1
(c) – 1
(d) 2

(ii) If $A=\left[\begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]$ then prove that $A^{2}=\left[\begin{array}{cc} \cos 2 \theta & \sin 2 \theta \\ -\sin 2 \theta & \cos 2 \theta \end{array}\right]$
$\text { (iii) if } A=\left[\begin{array}{ll} 1 & 3 \\ 4 & 1 \end{array}\right], \text { then find }\left|3 A^{T}\right|$ (March – 2017)
Answer:

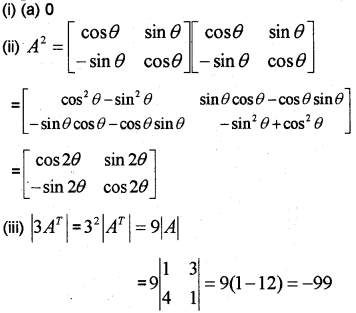
Plus Two Maths Matrices 6 Marks Important Questions

Question 1.
Let A be a matrix of order 3 x 3 whose elements are given by a_ij = 21 – j
(i) Obtain the matrix A.
(ii) Find AT Also express A as the sum of symmetric and skew-symmetric matrix. (March – 2010)
Answer:

Question 2.
Consider a 2 x 2 matrix $A=\left[a_{\theta}\right]$ with a_ij = 2ⁱ + j
(i) Construct A.
(ii) Find A + A^T, A – A^T
(iii) Express A as sum of a symmetric and skew-symmetric matrix. (May -2015)
Answer:

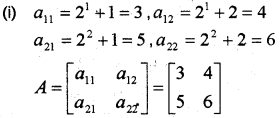
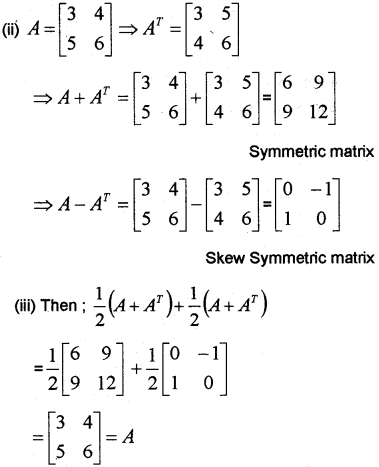
Question 3.
(i) $A=\left[\begin{array}{ll} 0 & 1 \\ 0 & 0 \end{array}\right], B=\left[\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right]$ then BA = _____
$\begin{array}{l} \text { (a) }\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right] & \text { (b) }\left[\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right] \\ \text { (c) }\left[\begin{array}{ll} 0 & 1 \\ 0 & 0 \end{array}\right] & \text { (d) }\left[\begin{array}{ll} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array}$

(ii) Write $A=\left[\begin{array}{cc} 3 & 5 \\ 1 & -1 \end{array}\right]$ as the sum of a symmetric and a skew symmetric matrix.
(iii) Find the inverse of $A=\left[\begin{array}{ll} 2 & -6 \\ 1 & -2 \end{array}\right]$ (March 2016)
Answer:

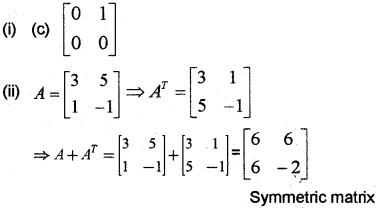
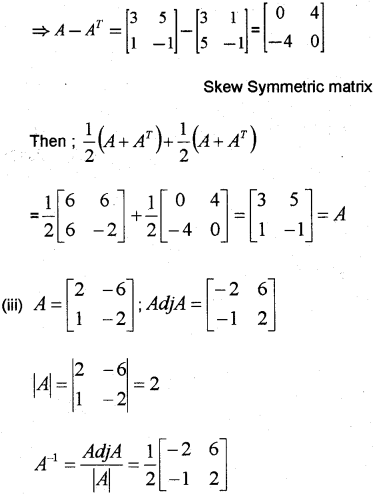
Question 4.
(i) If the matrix A is both symmetric and skew-symmetric, then A is a
(a) diagonal matrix
(b) zero matrix
(c) square matrix
(d) scalar matrix

(ii) If $A=\left[\begin{array}{cc} 1 & 3 \\ -2 & 4 \end{array}\right]$, then show that

(iii) Hence find A^-1 (May 2016)
Answer:

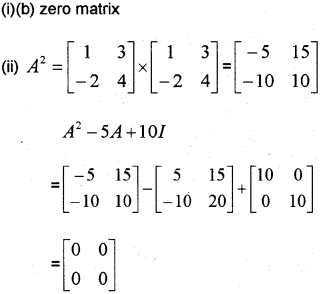
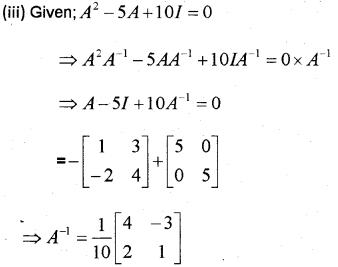
Question 5.
(i) The number of all possible 2 x 2 matrices with entries O or 1 is
(a) 8
(b) 9
(c) 16
(d) 25

(ii) If the area of a triangle whose vertices are (k,0), (5,0), (0,1) is 10 square units the find k.
(iii) Using elementary transformations find the inverse of the matrix $\left[\begin{array}{ll} 2 & 1 \\ 1 & 1 \end{array}\right]$ (May 2017)
Answer:

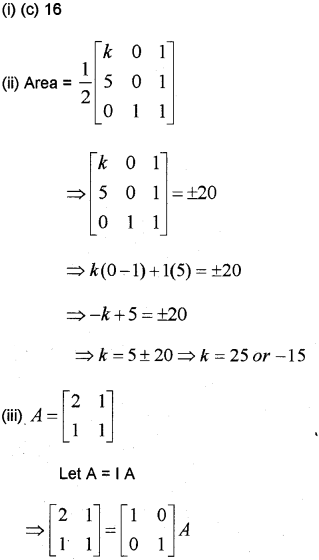
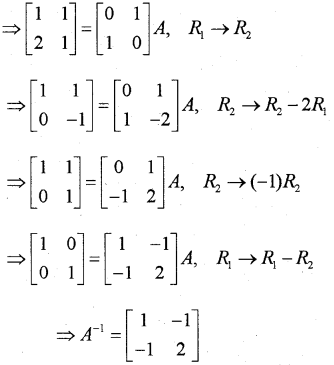
We hope the Plus Two Maths Chapter Wise Previous Questions Chapter 3 Matrices help you. If you have any query regarding Kerala Plus Two Maths Chapter Wise Previous Questions Chapter 3 Matrices, drop a comment below and we will get back to you at the earliest.